初中数学浙教版八年级下学期期末复习专题16.反比例函数的性质与图象
试卷更新日期:2021-06-27 类型:复习试卷
一、单选题
-
1. 下列函数中是反比例函数的是( )A、y=x+1 B、y= C、y=﹣2x D、y=2x22. 反比例函数 的图象一定不经过点( )A、(2,-3) B、(-2,3) C、(3,2) D、(-1,6)3. 已知反比例函数 ( )的图像上有两点A( , ),B( , ),且 ,
则 的值是( )
A、正数 B、负数 C、非正数 D、不能确定4. 函数 与函数 (k≠0)再同一直角坐标系中的大致图像可能是( )A、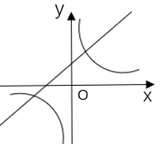 B、
B、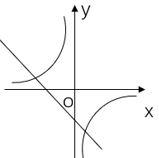 C、
C、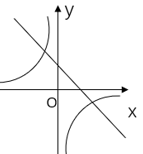 D、
D、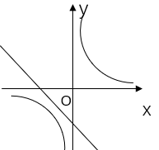 5. 已知点A(x1 , y1),B(x2 , y2)在反比例函数 的图象上,若y1<y2<0,则下列结论正确的是( )A、x1<x2<0 B、x2<x1<0 C、0<x1<x2 D、0<x2<x16. 如图,A(a,b)、B(-a,-b)是反比例函数 的图象上的两点.分别过点A、B作y轴的平行线,与反比例函数 的图象交于点C、D.若四边形ACBD的面积是4,则m、n满足等式( )
5. 已知点A(x1 , y1),B(x2 , y2)在反比例函数 的图象上,若y1<y2<0,则下列结论正确的是( )A、x1<x2<0 B、x2<x1<0 C、0<x1<x2 D、0<x2<x16. 如图,A(a,b)、B(-a,-b)是反比例函数 的图象上的两点.分别过点A、B作y轴的平行线,与反比例函数 的图象交于点C、D.若四边形ACBD的面积是4,则m、n满足等式( )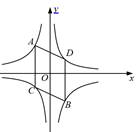 A、m+n=4 B、n-m=4 C、m+n=2 D、n-m=27. 如图,点 P 是反比例函数 y =6/x的图象上的任意一点,过点 P分别作两坐标轴的垂线,与坐标轴构成矩形 OAPB,点 D 是矩形OAPB 内任意一点,连接 DA、DB、DP、DO,则图中阴影 部分的面积( )
A、m+n=4 B、n-m=4 C、m+n=2 D、n-m=27. 如图,点 P 是反比例函数 y =6/x的图象上的任意一点,过点 P分别作两坐标轴的垂线,与坐标轴构成矩形 OAPB,点 D 是矩形OAPB 内任意一点,连接 DA、DB、DP、DO,则图中阴影 部分的面积( )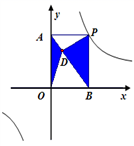 A、1 B、2 C、3 D、48. 已知反比例函数y=﹣ ,下列结论不正确的是( )A、图象必经过点(﹣1,2) B、y随x的增大而增大 C、图象在第二、四象限内 D、若x>1,则﹣2<y<09. 下列说法中错误的是( )A、有一组邻边相等的矩形是正方形 B、在反比例函数 中,y随x的增大而减小 C、顺次连接矩形各边中点得到的四边形是菱形 D、如果用反证法证明“三角形中至少有一个内角小于或等于60°”,首先应假设这个三角形中每一个内角都大于60°10. 如图,平行四边形ABCD的一边AB∥y轴,顶点B在x轴上,顶点A,C在双曲线y1= (k1>0,x>0)上,顶点D在双曲线y2= (k2>0,x>0)上,其中点C的坐标为(3,1),当四边形ABCD的面积为 时,k2的值是( )
A、1 B、2 C、3 D、48. 已知反比例函数y=﹣ ,下列结论不正确的是( )A、图象必经过点(﹣1,2) B、y随x的增大而增大 C、图象在第二、四象限内 D、若x>1,则﹣2<y<09. 下列说法中错误的是( )A、有一组邻边相等的矩形是正方形 B、在反比例函数 中,y随x的增大而减小 C、顺次连接矩形各边中点得到的四边形是菱形 D、如果用反证法证明“三角形中至少有一个内角小于或等于60°”,首先应假设这个三角形中每一个内角都大于60°10. 如图,平行四边形ABCD的一边AB∥y轴,顶点B在x轴上,顶点A,C在双曲线y1= (k1>0,x>0)上,顶点D在双曲线y2= (k2>0,x>0)上,其中点C的坐标为(3,1),当四边形ABCD的面积为 时,k2的值是( )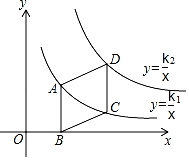 A、7.5 B、9 C、10.5 D、21
A、7.5 B、9 C、10.5 D、21二、填空题
-
11. 如果 是反比例函数,则k=.12. 如图,点A在反比例函数 (x>0)的图象上,过点A作AB⊥x轴,垂足为B,交反比例函数 (x>0)的图象于点C.P为y轴上一点,连接PA,PC.则△APC的面积为.
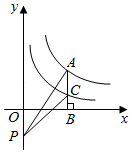 13. 如果反比例函数 的图像在每个象限内, 随着 的增大而减小,那么 的取值范围是 .14. 如图, , , 是反比例函数 在第一象限的图象上的点,它们的横坐标分别为2,4,6.过点 , , 分别作 轴, 轴的垂线段,构成多个矩形.若图中阴影部分的面积为12,则点 的坐标为.
13. 如果反比例函数 的图像在每个象限内, 随着 的增大而减小,那么 的取值范围是 .14. 如图, , , 是反比例函数 在第一象限的图象上的点,它们的横坐标分别为2,4,6.过点 , , 分别作 轴, 轴的垂线段,构成多个矩形.若图中阴影部分的面积为12,则点 的坐标为.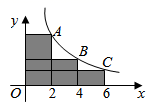 15. 如图,等边三角形ABO的顶点A在反比例函数y= (x<0)的图象上,边BO在x轴上,等边三角形ABO的面积为 ,则k=.
15. 如图,等边三角形ABO的顶点A在反比例函数y= (x<0)的图象上,边BO在x轴上,等边三角形ABO的面积为 ,则k=.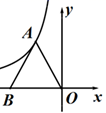 16. 已知反比例函数 的图像上三个点的坐标分别是 、 ,则 的大小关系的是 (用“<”号连接)
16. 已知反比例函数 的图像上三个点的坐标分别是 、 ,则 的大小关系的是 (用“<”号连接)三、解答题
-
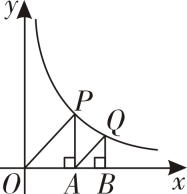
17. 已知 , 与 成反比例, 与 成正比例,且 =3时, =5; =1时, =-1.求 与 之间的函数关系式.18. 如图,△OAP、△ABQ是等腰直角三角形,点P、Q在函数 (k≠0)第一象限的图像上,直角顶点A、B均在x轴上,若OA=3,求点Q的坐标.
 19. 已知:如图,点A在反比例函数 的图像上,且点A的横坐标为2,作 垂直于x轴,垂足为点H, .
19. 已知:如图,点A在反比例函数 的图像上,且点A的横坐标为2,作 垂直于x轴,垂足为点H, .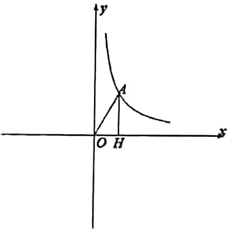 (1)、求 的长;(2)、求k的值;(3)、若 、 在该函数图象上,当 时,比较 与 的大小关系.20. 如图,点 , 分别在反比例函数 , 在第一象限的图象上,点 是 轴正半轴上一点,连结 , , .已知四边形 是平行四边形,且 , 两点的纵坐标之比为 .
(1)、求 的长;(2)、求k的值;(3)、若 、 在该函数图象上,当 时,比较 与 的大小关系.20. 如图,点 , 分别在反比例函数 , 在第一象限的图象上,点 是 轴正半轴上一点,连结 , , .已知四边形 是平行四边形,且 , 两点的纵坐标之比为 .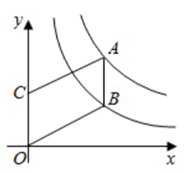 (1)、求 的值;(2)、当 是菱形时,求 的长.21. 函数揭示了两个变量之间的关系,它的表示方法有三种:表格法、图象法、解析式法请你根据学习函数的经验,完成对函数, 的探究.下表是函数 与自变量 的几组对应值:
(1)、求 的值;(2)、当 是菱形时,求 的长.21. 函数揭示了两个变量之间的关系,它的表示方法有三种:表格法、图象法、解析式法请你根据学习函数的经验,完成对函数, 的探究.下表是函数 与自变量 的几组对应值:···
-3
-2
-1
0
2
3
4
5
···
···
-0.5
-1
-2
-5
7
4
3
2.5
···
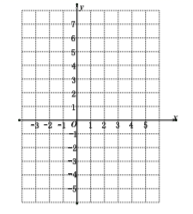 (1)、函数 自变量 的取值范围为(2)、根据表格中的数据,得 , 并在右面平面 直角坐标系 中,画出该函数的图象.(3)、请根据画出的函数图象,直接写出该函数的一条性质:(4)、利用所学函数知识,仔细观察上面表格和函数图象,直接写出不等式 的解集为22. 我们已经学习过反比例函数y= 的图像和性质,请你回顾研究它的过程,运用所学知识对函数 的图像和性质进行探索,并解决下列问题:(1)、该函数的图象大致是( )A、
(1)、函数 自变量 的取值范围为(2)、根据表格中的数据,得 , 并在右面平面 直角坐标系 中,画出该函数的图象.(3)、请根据画出的函数图象,直接写出该函数的一条性质:(4)、利用所学函数知识,仔细观察上面表格和函数图象,直接写出不等式 的解集为22. 我们已经学习过反比例函数y= 的图像和性质,请你回顾研究它的过程,运用所学知识对函数 的图像和性质进行探索,并解决下列问题:(1)、该函数的图象大致是( )A、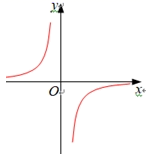 B、
B、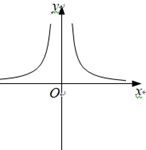 C、
C、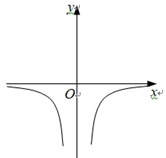 D、
D、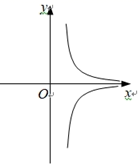 (2)、写出该函数两条不同类型的性质:
(2)、写出该函数两条不同类型的性质:①;
②.
(3)、写出不等式- +4>0的解集.23. 如图,在平面直角坐标系中, 四边形ABCD是矩形,AD∥x轴,A(-6,3),AB=2,AD=4。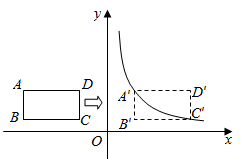 (1)、填空:点B的坐标是;点D的坐标是;(2)、将矩形ABCD向右平移m个单位,使点A,C恰好同时落在反比例函数y= (x>0) 的图象上, 得矩形A'B'C'D'。求矩形ABCD的平移距离m和反比例函数的解析式。24. 如图,在平面直角坐标系中,四边形ABCD是平行四边形,点A、B在x轴上,点C、D在第二象限,点M是BC中点.已知AB=6,AD=8,∠DAB=60°,点B的坐标为(-6,0).
(1)、填空:点B的坐标是;点D的坐标是;(2)、将矩形ABCD向右平移m个单位,使点A,C恰好同时落在反比例函数y= (x>0) 的图象上, 得矩形A'B'C'D'。求矩形ABCD的平移距离m和反比例函数的解析式。24. 如图,在平面直角坐标系中,四边形ABCD是平行四边形,点A、B在x轴上,点C、D在第二象限,点M是BC中点.已知AB=6,AD=8,∠DAB=60°,点B的坐标为(-6,0).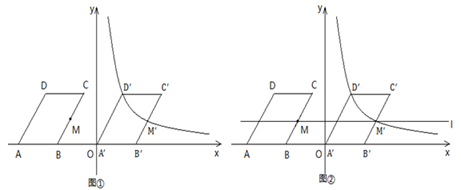 (1)、求点D和点M的坐标;(2)、如图①,将▱ABCD沿着x轴向右平移a个单位长度,点D的对应点 和点M的对应点 恰好在反比例函数 (x>0)的图像上,请求出a的值以及这个反比例函数的表达式;(3)、如图②,在(2)的条件下,过点M, 作直线l,点P是直线l上的动点,点Q是平面内任意一点,若以 ,P、Q为顶点的四边形是矩形,请直接写出所有满足条件的点Q的坐标.
(1)、求点D和点M的坐标;(2)、如图①,将▱ABCD沿着x轴向右平移a个单位长度,点D的对应点 和点M的对应点 恰好在反比例函数 (x>0)的图像上,请求出a的值以及这个反比例函数的表达式;(3)、如图②,在(2)的条件下,过点M, 作直线l,点P是直线l上的动点,点Q是平面内任意一点,若以 ,P、Q为顶点的四边形是矩形,请直接写出所有满足条件的点Q的坐标.