初中数学浙教版八年级下学期期末复习专题15 正方形的性质与判定
试卷更新日期:2021-06-27 类型:复习试卷
一、单选题
-
1. 下列不能判断是正方形的有( )A、对角线互相垂直的矩形 B、对角线相等的矩形 C、对角线互相垂直且相等的平行四边形 D、对角线相等的菱形2. 如图,已知四边形ABCD是正方形,E是AB延长线上一点,且BE=BD,则∠BDE的度数是( )
 A、22.5° B、30° C、45° D、67.5°3. 如图1是边长分别为 的两个正方形,经如图2所示的割补可以得到边长为 的正方形,且面积等于割补前的两正方形的面积之和.利用这个方法可以推得或验证勾股定理.现请你通过对图2的观察指出下面对割补过程的理解错误的是( )
A、22.5° B、30° C、45° D、67.5°3. 如图1是边长分别为 的两个正方形,经如图2所示的割补可以得到边长为 的正方形,且面积等于割补前的两正方形的面积之和.利用这个方法可以推得或验证勾股定理.现请你通过对图2的观察指出下面对割补过程的理解错误的是( ) A、割⑤补⑥ B、割③补① C、割①补④ D、割③补②4. 如图,正方形ABCD中,E、F是对角线AC上两点,连接BE、BF、DE、DF , 则添加下列条件①∠ABE=∠CBF;②AE=CF;③AB=AF;④BE=BF . 可以判定四边形BEDF是菱形的条件有( )
A、割⑤补⑥ B、割③补① C、割①补④ D、割③补②4. 如图,正方形ABCD中,E、F是对角线AC上两点,连接BE、BF、DE、DF , 则添加下列条件①∠ABE=∠CBF;②AE=CF;③AB=AF;④BE=BF . 可以判定四边形BEDF是菱形的条件有( )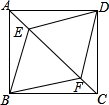 A、1个 B、2个 C、3个 D、4个5. 如图,点 、 分别是正方形 的边 、 上的点,且 , 、 相交于点 ,下列结论:① ;② ;③ ,其中一定正确的有( )
A、1个 B、2个 C、3个 D、4个5. 如图,点 、 分别是正方形 的边 、 上的点,且 , 、 相交于点 ,下列结论:① ;② ;③ ,其中一定正确的有( ) A、0个 B、1个 C、2个 D、3个6. 已知四边形 是平行四边形,下列条件:① ;② ;③ ;④ .选两个作为补充条件,使得四边形 是正方形,其中错误的选法是( )A、①② B、②③ C、①③ D、③④7. 四边形ABCD的对角线AC、BD交于点O , 能判定它是正方形的是( )A、AO=OC , OB=OD B、AO=BO=CO=DO , AC⊥BD C、AO=OC , OB=OD , AC⊥BD D、AO=OC=OB=OD8. 如图,把一个长方形的纸片对折两次,然后剪下一个角,要得到一个正方形,剪口与折痕所成锐角的大小为( )
A、0个 B、1个 C、2个 D、3个6. 已知四边形 是平行四边形,下列条件:① ;② ;③ ;④ .选两个作为补充条件,使得四边形 是正方形,其中错误的选法是( )A、①② B、②③ C、①③ D、③④7. 四边形ABCD的对角线AC、BD交于点O , 能判定它是正方形的是( )A、AO=OC , OB=OD B、AO=BO=CO=DO , AC⊥BD C、AO=OC , OB=OD , AC⊥BD D、AO=OC=OB=OD8. 如图,把一个长方形的纸片对折两次,然后剪下一个角,要得到一个正方形,剪口与折痕所成锐角的大小为( )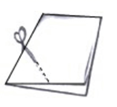 A、 B、 C、 D、9. 如图,在 中, , , , 与 的平分线交于点 ,过点 作 于点 ,若则 的长为( )
A、 B、 C、 D、9. 如图,在 中, , , , 与 的平分线交于点 ,过点 作 于点 ,若则 的长为( ) A、 B、2 C、 D、410. 如图,在 中, ,以 的各边为边分别作正方形 ,正方形 与正方形 .延长 , 分别交 , 于点K,J,连结 , .图中两块阴影部分面积分别记为 , ,若 ,四边形 ,则四边形 的面积为( )
A、 B、2 C、 D、410. 如图,在 中, ,以 的各边为边分别作正方形 ,正方形 与正方形 .延长 , 分别交 , 于点K,J,连结 , .图中两块阴影部分面积分别记为 , ,若 ,四边形 ,则四边形 的面积为( )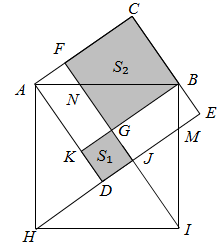 A、5 B、6 C、8 D、9
A、5 B、6 C、8 D、9二、填空题
-
11. 若一个正方形的面积为a2+a+ ,则此正方形的周长为.12. 已知正方形ABCD在直角坐标系中,A(2,2),B(4,2).那么C点的坐标为 .13. 如图,正方形ABCD的对角线长为8,E为AB上一点,若EF⊥AC于点F,EG⊥BD于点G,则EF+EG=.
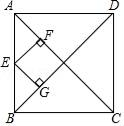 14. 如图,四边形ABCD是矩形,则只须补充条件(用字母表示只添加一个条件)就可以判定四边形ABCD是正方形.
14. 如图,四边形ABCD是矩形,则只须补充条件(用字母表示只添加一个条件)就可以判定四边形ABCD是正方形.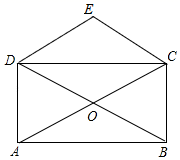 15. 如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则 的值为 .
15. 如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则 的值为 . 16. 在我国古算书《周髀算经》中记载周公与商高的谈话,其中就有勾股定理的最早文字记录,即“勾三股四弦五”,亦被称作商高定理.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的, ,AB=3,AC=4,则D,E,F,G,H,I都在矩形KLMJ的边上,那么矩形KLMJ的面积为.
16. 在我国古算书《周髀算经》中记载周公与商高的谈话,其中就有勾股定理的最早文字记录,即“勾三股四弦五”,亦被称作商高定理.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的, ,AB=3,AC=4,则D,E,F,G,H,I都在矩形KLMJ的边上,那么矩形KLMJ的面积为.
三、解答题
-
17. 如图,正方形ABCD的对角线AC,BD相交于点O.E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OG=OE.
 18. 如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM^AD,PN^CD,垂 足分别为M、N. 若∠ADC=90°,求证:四边形MPND是正方形.
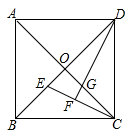
18. 如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM^AD,PN^CD,垂 足分别为M、N. 若∠ADC=90°,求证:四边形MPND是正方形. 19. 如图,在正方形 中,点 是对角线 上的一点,过点 作 交 于点 ,作 交 于点 .求证:
19. 如图,在正方形 中,点 是对角线 上的一点,过点 作 交 于点 ,作 交 于点 .求证: 20. 某课外活动小组对课本上的一道习题学习后,进行了拓展应用:
20. 某课外活动小组对课本上的一道习题学习后,进行了拓展应用: (1)、如图1,是在直线l上找一点P,使得PA+PB最短(画图即可).(2)、如图2,应用:已知正方形ABCD中,E为AB的中点,在线段BD上找一点P,使得PA+PE的值最小,画图即可.(3)、探索:E为正方形ABCD的AB边的中点,如图3,M为BC上一点,N为CD上一点,连接EM,MN,NA,请你应用(1)的原理,在图2中找出点M,N,使得EM+MN+NA的值最小,画图即可.21. △ABC中,点O是AC上一动点,过点O作直线MN∥BC,若MN交∠BCA的平分线于点E,交∠DCA的平分线于点F,连接AE、AF.
(1)、如图1,是在直线l上找一点P,使得PA+PB最短(画图即可).(2)、如图2,应用:已知正方形ABCD中,E为AB的中点,在线段BD上找一点P,使得PA+PE的值最小,画图即可.(3)、探索:E为正方形ABCD的AB边的中点,如图3,M为BC上一点,N为CD上一点,连接EM,MN,NA,请你应用(1)的原理,在图2中找出点M,N,使得EM+MN+NA的值最小,画图即可.21. △ABC中,点O是AC上一动点,过点O作直线MN∥BC,若MN交∠BCA的平分线于点E,交∠DCA的平分线于点F,连接AE、AF.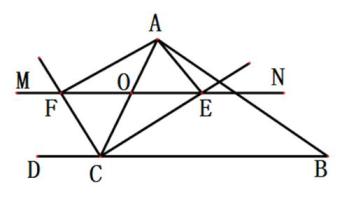 (1)、说明:OE=OF(2)、当点O运动到AC中点处时,求证:四边形AECF是矩形;(3)、在(2)的条件下,当△ABC满足什么条件时,四边形AECF为正方形,并加以证明.22. 下面我们做一次折叠活动:
(1)、说明:OE=OF(2)、当点O运动到AC中点处时,求证:四边形AECF是矩形;(3)、在(2)的条件下,当△ABC满足什么条件时,四边形AECF为正方形,并加以证明.22. 下面我们做一次折叠活动:
第一步,在一张宽为2的矩形纸片的一端,利用图(1)的方法折出一个正方形,然后把纸片展平,折痕为MC;
第二步,如图(2),把这个正方形折成两个相等的矩形,再把纸片展平,折痕为FA;
第三步,折出内侧矩形FACB的对角线AB,并将AB折到图(3)中所示的AD处,折痕为AQ.
根据以上的操作过程,完成下列问题:
(1)、求CD的长.(2)、请判断四边形ABQD的形状,并说明你的理由.

