初中数学浙教版八年级下学期期末复习专题14 菱形的性质与判定
试卷更新日期:2021-06-27 类型:复习试卷
一、单选题
-
1. 已知菱形ABCD的周长为16,则菱形ABCD的边长为( )A、4 B、8 C、12 D、22. 如图,在菱形 中, 相交于 , , 是线段 上一点,则 的度数可能是( )
 A、 B、 C、 D、3. 如图,在菱形ABCD中,对角线BD=4,AC=3BD,则菱形ABCD的面积为( )
A、 B、 C、 D、3. 如图,在菱形ABCD中,对角线BD=4,AC=3BD,则菱形ABCD的面积为( ) A、96 B、48 C、24 D、64. 菱形的一个内角是 ,边长是 ,则这个菱形的较短的对角线长是( )A、 B、 C、 D、5. 下面性质中,菱形不一定具备的是( )A、四条边都相等 B、每一条对角线平分一组对角 C、邻角互补 D、对角线相等6. 如图,在菱形ABCD中,AC与BD相交于点O,点P是AB的中点,PO=2,则菱形ABCD的周长是( )
A、96 B、48 C、24 D、64. 菱形的一个内角是 ,边长是 ,则这个菱形的较短的对角线长是( )A、 B、 C、 D、5. 下面性质中,菱形不一定具备的是( )A、四条边都相等 B、每一条对角线平分一组对角 C、邻角互补 D、对角线相等6. 如图,在菱形ABCD中,AC与BD相交于点O,点P是AB的中点,PO=2,则菱形ABCD的周长是( )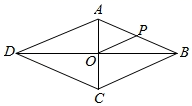 A、4 B、8 C、16 D、247. 如图,在平行四边形ABCD中,点F是AB的中点,连接DF并延长,交CB的延长线于点E , 连接AE . 添加一个条件,使四边形AEBD是菱形,这个条件是( )
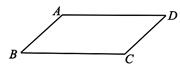
A、4 B、8 C、16 D、247. 如图,在平行四边形ABCD中,点F是AB的中点,连接DF并延长,交CB的延长线于点E , 连接AE . 添加一个条件,使四边形AEBD是菱形,这个条件是( ) A、 B、 C、 D、DE平分8. 如图,在一张平行四边形纸片ABCD中,画一个菱形,甲、乙两位同学的画法如下:
A、 B、 C、 D、DE平分8. 如图,在一张平行四边形纸片ABCD中,画一个菱形,甲、乙两位同学的画法如下:甲:以B , A为圆心,AB长为半径作弧,分别交BC , AD于点E , F , 则四边形ABEF为菱形;乙:作∠A , ∠B的平分线AE , BF , 分别交BC于点E , 交AD于点F , 则四边形ABEF是菱形;关于甲、乙两人的画法,下列判断正确的是( )
 A、仅甲正确 B、仅乙正确 C、甲、乙均正确 D、甲、乙均错误9. 在四边形 中,对角线 和 交于点 ,下列条件能判定这个四边形是菱形的是( )A、 , B、 , , C、 , , D、 , ,10. 有两张宽为3,长为9的矩形纸片如图所示叠放在一起,使重叠的部分构成一个四边形,则四边形的最大面积是( )
A、仅甲正确 B、仅乙正确 C、甲、乙均正确 D、甲、乙均错误9. 在四边形 中,对角线 和 交于点 ,下列条件能判定这个四边形是菱形的是( )A、 , B、 , , C、 , , D、 , ,10. 有两张宽为3,长为9的矩形纸片如图所示叠放在一起,使重叠的部分构成一个四边形,则四边形的最大面积是( ) A、27 B、12 C、15 D、18
A、27 B、12 C、15 D、18二、填空题
-
11. 已知菱形的周长为20,一条对角线长为8,则菱形的面积为 .12. 两个全等菱形如图所示摆放在一起,其中 和 分别在同一条直线上,若较短的对角线长为10,点 与点 的距离是24,则此菱形边长为.
 13. 如图,在菱形 中, 、 相交于点O, , 长为4,则菱形 的面积是.
13. 如图,在菱形 中, 、 相交于点O, , 长为4,则菱形 的面积是.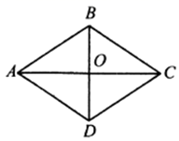 14. 如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC,BD相交于点O,点E在AB上,且BE=BO,则∠EOA=°.
14. 如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC,BD相交于点O,点E在AB上,且BE=BO,则∠EOA=°. 15. 如图,在 中, 于点 点 分别是 边的中点,请你在 中添加一个条件: , 使得四边形 是菱形.
15. 如图,在 中, 于点 点 分别是 边的中点,请你在 中添加一个条件: , 使得四边形 是菱形.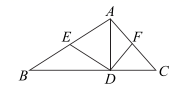 16. 如图,CD与BE互相垂直平分,AD⊥DB,∠BDE=70°,则∠CAD=°.
16. 如图,CD与BE互相垂直平分,AD⊥DB,∠BDE=70°,则∠CAD=°.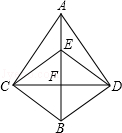
三、解答题
-
17. 菱形ABCD中,对角线AC和BD相交于O,已知AC=8,BD=6,求AB边上的高.
 18. 如图,在□ 中,E、F分别是 , 边上的点,且 .当 时,求证:四边形 是菱形.
18. 如图,在□ 中,E、F分别是 , 边上的点,且 .当 时,求证:四边形 是菱形. 19. 如图,四边形ABCD中,AD∥BC,AB⊥AC,点E是BC的中点,AE与BD交于点F,且F是AE的中点.
19. 如图,四边形ABCD中,AD∥BC,AB⊥AC,点E是BC的中点,AE与BD交于点F,且F是AE的中点.(Ⅰ)求证:四边形AECD是菱形;(Ⅱ)若AC=4,AB=5,求四边形ABCD的面积.
 20. 如图,菱形花坛 的一边长 为 , ,沿着该菱形的对角线修建两条小路 和 .
20. 如图,菱形花坛 的一边长 为 , ,沿着该菱形的对角线修建两条小路 和 . (1)、求 和 的长;(2)、求菱形花坛 的面积.21. 老师布置了一个作业,如下:
(1)、求 和 的长;(2)、求菱形花坛 的面积.21. 老师布置了一个作业,如下:已知:如图1 的对角线 的垂直平分线 交 于点 ,交 于点 ,交 于点 .求证:四边形 是菱形.
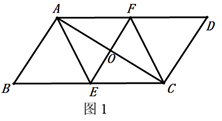

嘉琪同学写出了如图2所示的证明过程,老师说嘉琪同学的作业是错误的.请你解答下列问题:
(1)、能找出该同学错误的原因吗?请你指出来;(2)、请你给出本题的符合题意证明过程.22. 如图所示的正方形网格中,每个小正方形的边长都是1个单位长度,线段AB的端点都在正方形网格的格点上. (1)、请在下面的网格中作出菱形ABCD(点C,D都在正方形网格的格点上,作出一个正确的图形即可);(2)、在(1)中作出的菱形面积是 .
(1)、请在下面的网格中作出菱形ABCD(点C,D都在正方形网格的格点上,作出一个正确的图形即可);(2)、在(1)中作出的菱形面积是 .

