初中数学浙教版八年级下学期期末复习专题13 矩形的性质与判定

试卷更新日期：2021-06-27 类型：复习试卷

进入出卷网下载

一、单选题

1. 数学课上，老师要同学们判断一个四边形门框是否为矩形．下面是某合作小组4位同学拟定的方案，其中正确的是（）

A、测量对角线是否互相平分 B、测量两组对边是否分别相等 C、测量一组对角是否都为直角 D、测量三个角是否为直角

查看试题解析
2. 如图，在 $▱$ ABCD中，对角线AC、BD相交于点O，OA=3cm，若要使平行四边形ABCD为矩形，则OB的长度为（）

A、4cm B、3cm C、2cm D、1cm

查看试题解析
3. 如图，小明将一张长为 $20 cm$ ，宽为 $15 cm$ 的长方形纸 $(A E > D E)$ 剪去了一角，量得 $A B = 3 cm$ ， $C D = 4 cm$ ，则 $BC$ 长为（）

A、 $20 cm$ B、 $16 cm$ C、 $12 cm$ D、 $5 cm$

查看试题解析
4. 如图，矩形ABCD中，对角线AC、BD相交于点O，过点O作OE⊥BD交AD于点E，已知AB=2， $S_{△ D O E} = \frac{5}{4}$ ，则AE的长为（）

A、1.5 B、2 C、2.5 D、 $\sqrt{2}$

查看试题解析
5. 如图，长方形ABCD是由6个正方形组成，其中有两个一样大的正方形，且最小正方形边长为1，则长方形ABCD的边长DC为（）

A、10 B、13 C、16 D、19

查看试题解析
6. 矩形 $A B C D$ 的两条对角线相交于O点， $∠ A O B = 60 °$ ，若 $B C = 6$ ，则矩形的对角线 $A C$ 的长为（）

A、2 B、4 C、 $2 \sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析
7. 如图， $▱ A B C D$ 的对角线 $A C$ ， $B D$ 相交于点O，添加下列条件后，不能得出四边形 $A B C D$ 是矩形的是（）

A、 $∠ D A B + ∠ D C B = 180 °$ B、 $A B^{2} + B C^{2} = A C^{2}$ C、 $A C = B D$ D、 $A C ⊥ B D$

查看试题解析
8. 下列命题中，能判断四边形是矩形的是（）

A、对角线相等 B、对角线互相平分 C、对角线相等且互相平分 D、对角线互相垂直

查看试题解析
9. 在▱ABCD中，对角线AC、BD相交于点O，若∠ABC＝90°，则下列结论错误的是（）

A、AC＝BD B、OA＝OB C、AC⊥BD D、AB＝CD

查看试题解析
10. 如图△ABC中，AC的垂直平分线分别交AC，AB于点D，F，BE⊥DF交DF的延长线于点E，已知∠A=30°，BC=2，AF=BF，则四边形BCDE的面积是（）

A、2 $\sqrt{3}$ B、3 $\sqrt{3}$ C、4 D、4 $\sqrt{3}$

查看试题解析

二、填空题

11. 在矩形ABCD中，AC与BD相交于点O，若OA＝2，则BD的长是.

查看试题解析
12. 如图，四边形 $A B C D$ 的对角线互相平分，请你添加一个条件，使它成为矩形，你添加的条件是．

查看试题解析
13. 长方形的宽为 $\sqrt{3}$ ，面积为6，则长方形的长为 .

查看试题解析
14. 矩形的一个角的平分线分一边为2和4两部分，则这个矩形的对角线的长．

查看试题解析
15. 如图，点E、F、G、H分别是矩形ABCD边AB、BC、CD、DA上的点，且HG与EF交于点I，连接HE、FG，若AB=6，BC=5，EF//AD，HG//AB，则HE+FG的最小值是．

查看试题解析
16. 如图，在矩形ABCD中，BC＝40cm，点P和点Q分别从点B和点D出发，按逆时针方向沿矩形ABCD的边运动，点P和点Q的速度分别为3cm/s和1cm/s，则最快s后，四边ABPQ成为矩形.

查看试题解析

三、解答题

17. 如图，延长矩形 $A B C D$ 的边 $B C$ 至点E，使 $C E = B D$ ，连接 $A E$ ， $A C$ ，求证： $A E$ 平分 $∠ C A D$ ．

查看试题解析
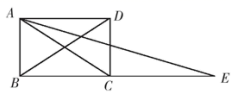18. 如图，△ABC中，AB=AC，AD是△ABC的角平分线，点O为AB的中点，连接DO并延长到点E，使OE=OD，连接AE，BE．

求证：四边形AEBD是矩形．

查看试题解析
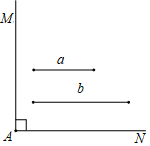
19. 已知：如图，∠MAN＝90°，线段a和线段b
求作：矩形ABCD，使得矩形ABCD的两条边长分别等于线段a和线段b．

下面是小东设计的尺规作图过程．

作法：如图，

①以点A为圆心，b为半径作弧，交AN于点B；

②以点A为圆心，a为半径作弧，交AM于点D；

③分别以点B、点D为圆心，a、b长为半径作弧，两弧交于∠MAN内部的点C；

④分别连接BC，DC．

所以四边形ABCD就是所求作的矩形．

根据小东设计的尺规作图过程，

(1)、使用直尺和圆规，补全图形；（保留作图痕迹）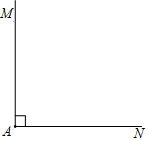

(2)、完成下面的证明．
证明：

∵AB＝；AD＝；

∴四边形ABCD是平行四边形．

∵∠MAN＝90°；

∴四边形ABCD是矩形（填依据）．

查看试题解析
20. 如图所示，在△ABC中，D是AC的中点，E是线段BC延长线上一点，过点A作BE的平行线与线段ED的延长线交于点F，连结AE、CF.

(1)、求证：AF＝CE；

(2)、若AC＝EF，试判断四边形AFCE是什么样的四边形，并证明你的结论．

查看试题解析
21. 如图，在▱ABCD中，AC＝8，BD＝12，点E、F在对角线BD上，点E从点B出发以1个单位每秒的速度向点D运动，同时点F从点D出发以相同速度向点B运动，到端点时运动停止，运动时间为t秒．

(1)、求证：四边形AECF为平行四边形．

(2)、求t为何值时，四边形AECF为矩形．

查看试题解析
22. 如图，在平行四边形 $A B C D$ 中， $C E ⊥ A D$ 于点 $E$ ，延长 $D A$ 至点 $F$ ，使得 $E F = D A$ ，连接 $B F$ ， $C F$ ．

(1)、求证：四边形 $B C E F$ 是矩形；

(2)、若 $A B = 3$ ， $C F = 4$ ， $D F = 5$ ，求 $E F$ 的长．

查看试题解析
23. 如图，在 $△ A B C$ 中，点O是 $A C$ 边上的一个动点，过点O作直线 $M N // B C$ ， $∠ A C B$ 以及外角 $∠ A C D$ 的平分线分别交 $M N$ 于点E、F.

(1)、求证： $O E = O F$ ；

(2)、当点O运动到 $A C$ 边的什么位置时，四边形 $A E C F$ 是矩形？回答并证明你的结论.

查看试题解析
24. 在四边形ABCD中，∠A=∠B=∠C=∠D=90°，AB=CD=10，BC=AD=6，P为射线BC上一点，将△ABP沿直线AP翻折至△AEP的位置，使点B落在点E处.

(1)、若P为BC上一点
a：如图1，当点E落在边CD上时，直接写出此时CE=.

b：如图2，连接CE，若CE $//$ AP，则BP与BC有何数量关系？请说明理由.

(2)、如图3，如果点P在BC的延长线上时，当△PEC为直角三角形时，求PB的长.

查看试题解析