浙江省衢州市2021年中考数学试卷
试卷更新日期:2021-06-25 类型:中考真卷
一、单选题
-
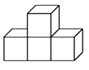
1. 21的相反数是( )A、 21 B、-21 C、- D、2. 如图是由四个相同的小正方体搭成的立体图形,它的主视图是( )
 A、
A、 B、
B、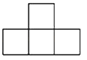 C、
C、 D、
D、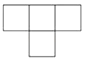 3. 2021年5月国家统计局公布了第七次人口普查结果,我国人口数约为1412000000,其中数据1412000000用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 一个布袋里放有3个红球和2个白球,它们除颜色外其余都相同.从布袋中任意摸出1个球,摸到白球的概率是( )A、 B、 C、 D、6. 已知扇形的半径为6,圆心角为 .则它的面积是( )A、 B、 C、 D、7. 如图,在 中, , , ,点D,E,F分别是AB,BC,CA的中点,连结DE,EF,则四边形ADEF的周长为( )
3. 2021年5月国家统计局公布了第七次人口普查结果,我国人口数约为1412000000,其中数据1412000000用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 一个布袋里放有3个红球和2个白球,它们除颜色外其余都相同.从布袋中任意摸出1个球,摸到白球的概率是( )A、 B、 C、 D、6. 已知扇形的半径为6,圆心角为 .则它的面积是( )A、 B、 C、 D、7. 如图,在 中, , , ,点D,E,F分别是AB,BC,CA的中点,连结DE,EF,则四边形ADEF的周长为( ) A、6 B、9 C、12 D、158. 《九章算术》是中国传统数学的重要著作,书中有一道题“今有五雀六燕,集称之衡,雀俱重,燕俱轻;一雀一燕交而处,衡适平;并燕雀重一斤.问:燕雀一枚,各重几何?”译文:”五只雀、六只燕,共重1斤(占时1斤=16两).雀重燕轻,互换其中一只,恰好一样重,问:每只雀、燕重量各为多少?”设雀重x两,燕重y两,可列出方程组( )A、 B、 C、 D、9. 如图.将菱形ABCD绕点A逆时针旋转 得到菱形 , .当AC平分 时, 与 满足的数量关系是( )
A、6 B、9 C、12 D、158. 《九章算术》是中国传统数学的重要著作,书中有一道题“今有五雀六燕,集称之衡,雀俱重,燕俱轻;一雀一燕交而处,衡适平;并燕雀重一斤.问:燕雀一枚,各重几何?”译文:”五只雀、六只燕,共重1斤(占时1斤=16两).雀重燕轻,互换其中一只,恰好一样重,问:每只雀、燕重量各为多少?”设雀重x两,燕重y两,可列出方程组( )A、 B、 C、 D、9. 如图.将菱形ABCD绕点A逆时针旋转 得到菱形 , .当AC平分 时, 与 满足的数量关系是( )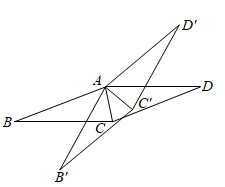 A、 B、 C、 D、10. 已知A,B两地相距60km,甲、乙两人沿同一条公路从A地出发到B地,甲骑自行车匀速行驶3h到达,乙骑摩托车.比甲迟1h出发,行至30km处追上甲,停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶时间x的函数图象如图所示.当乙再次追上甲时距离B地( )
A、 B、 C、 D、10. 已知A,B两地相距60km,甲、乙两人沿同一条公路从A地出发到B地,甲骑自行车匀速行驶3h到达,乙骑摩托车.比甲迟1h出发,行至30km处追上甲,停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶时间x的函数图象如图所示.当乙再次追上甲时距离B地( )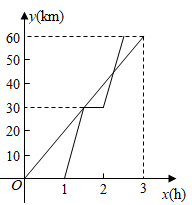 A、15km B、16km C、44km D、45km
A、15km B、16km C、44km D、45km二、填空题
-
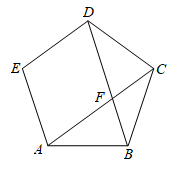
11. 若 有意义,则x的值可以是.(写出一个即可)12. 不等式 的解为.13. 为庆祝建党100周年,某校举行“庆百年红歌大赛”.七年级5个班得分分别为85,90,88,95,92,则5个班得分的中位数为分.14. 如图,在正五边形ABCDE中,连结AC,BD交于点F,则 的度数为.
 15. 将一副三角板如图放置在平面直角坐标系中,顶点A与原点O重合,AB在x轴正半轴上,且 ,点E在AD上, ,将这副三角板整体向右平移个单位,C,E两点同时落在反比例函数 的图象上.
15. 将一副三角板如图放置在平面直角坐标系中,顶点A与原点O重合,AB在x轴正半轴上,且 ,点E在AD上, ,将这副三角板整体向右平移个单位,C,E两点同时落在反比例函数 的图象上.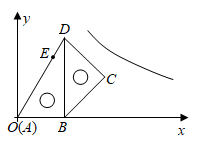 16. 图1是某折叠式靠背椅实物图,图2是椅子打开时的侧面示意图,椅面CE与地面平行,支撑杆AD,BC可绕连接点O转动,且 ,椅面底部有一根可以绕点H转动的连杆HD,点H是CD的中点,FA,EB均与地面垂直,测得 , , .
16. 图1是某折叠式靠背椅实物图,图2是椅子打开时的侧面示意图,椅面CE与地面平行,支撑杆AD,BC可绕连接点O转动,且 ,椅面底部有一根可以绕点H转动的连杆HD,点H是CD的中点,FA,EB均与地面垂直,测得 , , . (1)、椅面CE的长度为cm.(2)、如图3,椅子折叠时,连杆HD绕着支点H带动支撑杆AD,BC转动合拢,椅面和连杆夹角 的度数达到最小值 时,A,B两点间的距离为cm(结果精确到0.1cm).(参考数据: , , )
(1)、椅面CE的长度为cm.(2)、如图3,椅子折叠时,连杆HD绕着支点H带动支撑杆AD,BC转动合拢,椅面和连杆夹角 的度数达到最小值 时,A,B两点间的距离为cm(结果精确到0.1cm).(参考数据: , , )三、解答题
-
17. 计算: .18. 先化简,再求值: ,其中 .19. 如图,在 的网格中, 的三个顶点都在格点上.
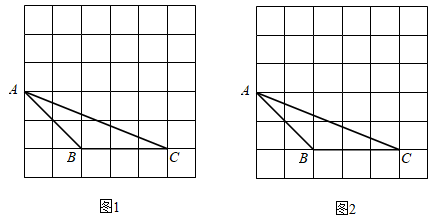 (1)、在图1中画出 ,使 与 全等,顶点D在格点上.(2)、在图2中过点B画出平分 面积的直线l.20. 为进一步做好“光盘行动”,某校食堂推出“半份菜”服务,在试行阶段,食堂对师生满意度进行抽样调查.并将结果绘制成如下统计图(不完整).
(1)、在图1中画出 ,使 与 全等,顶点D在格点上.(2)、在图2中过点B画出平分 面积的直线l.20. 为进一步做好“光盘行动”,某校食堂推出“半份菜”服务,在试行阶段,食堂对师生满意度进行抽样调查.并将结果绘制成如下统计图(不完整). (1)、求被调查的师生人数,并补全条形统计图,(2)、求扇形统计图中表示“满意”的扇形圆心角度数.(3)、若该校共有师生1800名,根据抽样结果,试估计该校对食堂“半份菜”服务“很满意”或“满意”的师生总人数.21. 如图,在 中, ,BC与 相切于点D,过点A作AC的垂线交CB的延长线于点E,交 于点F,连结BF.
(1)、求被调查的师生人数,并补全条形统计图,(2)、求扇形统计图中表示“满意”的扇形圆心角度数.(3)、若该校共有师生1800名,根据抽样结果,试估计该校对食堂“半份菜”服务“很满意”或“满意”的师生总人数.21. 如图,在 中, ,BC与 相切于点D,过点A作AC的垂线交CB的延长线于点E,交 于点F,连结BF. (1)、求证:BF是 的切线.(2)、若 , ,求EF的长.22. 如图1是一座抛物线型拱桥侧面示意图.水面宽AB与桥长CD均为24m,在距离D点6米的E处,测得桥面到桥拱的距离EF为1.5m,以桥拱顶点O为原点,桥面为x轴建立平面直角坐标系.
(1)、求证:BF是 的切线.(2)、若 , ,求EF的长.22. 如图1是一座抛物线型拱桥侧面示意图.水面宽AB与桥长CD均为24m,在距离D点6米的E处,测得桥面到桥拱的距离EF为1.5m,以桥拱顶点O为原点,桥面为x轴建立平面直角坐标系.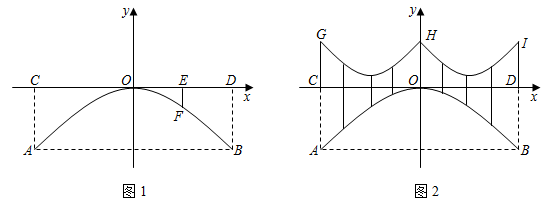 (1)、求桥拱项部O离水面的距离.(2)、如图2,桥面上方有3根高度均为4m的支柱CG,OH,DI,过相邻两根支柱顶端的钢缆呈形状相同的抛物线,其最低点到桥面距离为1m.
(1)、求桥拱项部O离水面的距离.(2)、如图2,桥面上方有3根高度均为4m的支柱CG,OH,DI,过相邻两根支柱顶端的钢缆呈形状相同的抛物线,其最低点到桥面距离为1m.①求出其中一条钢缆抛物线的函数表达式.
②为庆祝节日,在钢缆和桥拱之间竖直装饰若干条彩带,求彩带长度的最小值.
23. 如图1,点C是半圆O的直径AB上一动点(不包括端点), ,过点C作 交半圆于点D,连结AD,过点C作 交半圆于点E,连结EB.牛牛想探究在点C运动过程中EC与EB的大小关系.他根据学习函数的经验,记 , , .请你一起参与探究函数 、 随自变量x变化的规律.通过几何画板取点、画图、测量,得出如下几组对应值,并在图2中描出了以各对对应值为坐标的点,画出了不完整图象.
x … 0.30 0.80 1.60 2.40 3.20 4.00 4.80 5.60 … … 2.01 2.98 3.46 3.33 2.83 2.11 1.27 0.38 … … 5.60 4.95 3.95 2.96 2.06 1.24 0.57 0.10 … 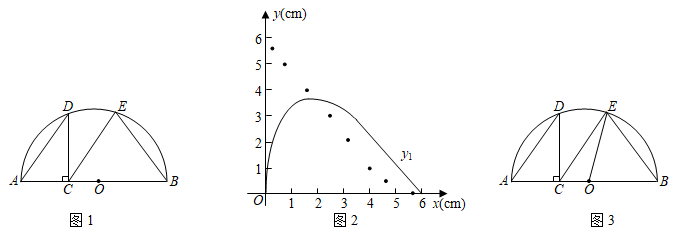 (1)、当 时, =.(2)、在图2中画出函数 的图象,并结合图象判断函数值 与 的大小关系.(3)、由(2)知“AC取某值时,有 ”.如图3,牛牛连结了OE,尝试通过计算EC,EB的长来验证这一结论,请你完成计算过程.24. 如图,
(1)、当 时, =.(2)、在图2中画出函数 的图象,并结合图象判断函数值 与 的大小关系.(3)、由(2)知“AC取某值时,有 ”.如图3,牛牛连结了OE,尝试通过计算EC,EB的长来验证这一结论,请你完成计算过程.24. 如图, (1)、【推理】
(1)、【推理】
如图1,在正方形ABCD中,点E是CD上一动点,将正方形沿着BE折叠,点C落在点F处,连结BE,CF,延长CF交AD于点G. 求证: .(2)、【运用】
如图2,在(推理)条件下,延长BF交AD于点H.若 , ,求线段DE的长.(3)、【拓展】
将正方形改成矩形,同样沿着BE折叠,连结CF,延长CF,BF交直线AD于G,两点,若 , ,求 的值(用含k的代数式表示).