四川省达州市2021年中考数学试卷
试卷更新日期:2021-06-25 类型:中考真卷
一、单选题
-
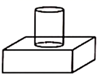
1. ﹣ 的相反数是( )A、﹣ B、﹣ C、 D、2. 如图,几何体是由圆柱和长方体组成的,它的主视图是( )
 A、
A、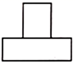 B、
B、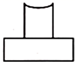 C、
C、 D、
D、 3. 实数 在数轴上的对应点可能是( )
3. 实数 在数轴上的对应点可能是( ) A、 点 B、 点 C、 点 D、 点4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,一束光线 先后经平面镜 , 反射后,反射光线 与 平行,当 时, 的度数为( )
A、 点 B、 点 C、 点 D、 点4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,一束光线 先后经平面镜 , 反射后,反射光线 与 平行,当 时, 的度数为( ) A、 B、 C、 D、6. 在反比例函数 ( 为常数)上有三点 , , ,若 ,则 , , 的大小关系为( )A、 B、 C、 D、7. 以下命题是假命题的是( )A、 的算术平方根是2 B、有两边相等的三角形是等腰三角形 C、一组数据:3, ,1,1,2,4的中位数是1.5 D、过直线外一点有且只有一条直线与已知直线平行8. 生活中常用的十进制是用0~9这十个数字来表示数,满十进一,例: , ;计算机也常用十六进制来表示字符代码,它是用0~ 来表示0~15,满十六进一,它与十进制对应的数如下表:
A、 B、 C、 D、6. 在反比例函数 ( 为常数)上有三点 , , ,若 ,则 , , 的大小关系为( )A、 B、 C、 D、7. 以下命题是假命题的是( )A、 的算术平方根是2 B、有两边相等的三角形是等腰三角形 C、一组数据:3, ,1,1,2,4的中位数是1.5 D、过直线外一点有且只有一条直线与已知直线平行8. 生活中常用的十进制是用0~9这十个数字来表示数,满十进一,例: , ;计算机也常用十六进制来表示字符代码,它是用0~ 来表示0~15,满十六进一,它与十进制对应的数如下表:十进制
0
1
2
…
8
9
10
11
12
13
14
15
16
17
…
十六进制
0
1
2
…
8
9
10
11
…
例:十六进制 对应十进制的数为 , 对应十进制的数为 ,那么十六进制中 对应十进制的数为( )
A、28 B、62 C、238 D、3349. 在平面直角坐标系中,等边 如图放置,点 的坐标为 ,每一次将 绕着点 逆时针方向旋转 ,同时每边扩大为原来的2倍,第一次旋转后得到 ,第二次旋转后得到 ,…,依次类推,则点 的坐标为( )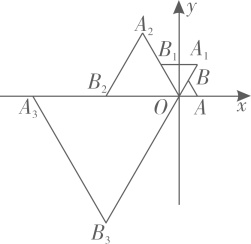 A、 B、 C、 D、10. 如图,已知抛物线 ( , , 为常数, )经过点 ,且对称轴为直线 ,有下列结论:① ;② ;③ ;④无论 , , 取何值,抛物线一定经过 ;⑤ .其中正确结论有( )
A、 B、 C、 D、10. 如图,已知抛物线 ( , , 为常数, )经过点 ,且对称轴为直线 ,有下列结论:① ;② ;③ ;④无论 , , 取何值,抛物线一定经过 ;⑤ .其中正确结论有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 截至2020年末,达州市金融精准扶贫共计392.5亿元,居全省第2,惠及建档立卡贫困户8.96万人.将392.5亿元用科学记数法表示应为元.12. 如图是一个运算程序示意图,若开始输入 的值为3,则输出 值为.
 13. 已知 , 满足等式 ,则 .14. 若分式方程 的解为整数,则整数 .15. 如图,在边长为6的等边 中,点 , 分别是边 , 上的动点,且 ,连接 , 交于点 ,连接 ,则 的最小值为.
13. 已知 , 满足等式 ,则 .14. 若分式方程 的解为整数,则整数 .15. 如图,在边长为6的等边 中,点 , 分别是边 , 上的动点,且 ,连接 , 交于点 ,连接 ,则 的最小值为.
三、解答题
-
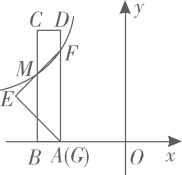
16. 如图,将一把矩形直尺 和一块等腰直角三角板 摆放在平面直角坐标系中, 在 轴上,点 与点 重合,点 在 上, 交 于点 ,反比例函数 的图象恰好经过点 , ,若直尺的宽 ,三角板的斜边 ,则 .
 17. 计算: .18. 化简求值: ,其中 与2,3构成三角形的三边,且 为整数.19. 为庆祝中国共产党成立100周年,在中小学生心中厚植爱党情怀,我市开展“童心向党”教育实践活动,某校准备组织学生参加唱歌,舞蹈,书法,国学诵读活动.为了解学生的参与情况,该校随机抽取了部分学生进行“你愿意参加哪一项活动”(必选且只选一种)的问卷调查.根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
17. 计算: .18. 化简求值: ,其中 与2,3构成三角形的三边,且 为整数.19. 为庆祝中国共产党成立100周年,在中小学生心中厚植爱党情怀,我市开展“童心向党”教育实践活动,某校准备组织学生参加唱歌,舞蹈,书法,国学诵读活动.为了解学生的参与情况,该校随机抽取了部分学生进行“你愿意参加哪一项活动”(必选且只选一种)的问卷调查.根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
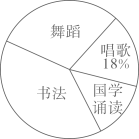 (1)、这次抽样调查的总人数为人,扇形统计图中“舞蹈”对应的圆心角度数为;(2)、若该校有1400名学生,估计选择参加书法的有多少人?(3)、学校准备从推荐的4位同学(两男两女)中选取2人主持活动,利用画树状图或表格法求恰为一男一女的概率.20. 如图,在平面直角坐标中, 的顶点坐标分别是 , , .
(1)、这次抽样调查的总人数为人,扇形统计图中“舞蹈”对应的圆心角度数为;(2)、若该校有1400名学生,估计选择参加书法的有多少人?(3)、学校准备从推荐的4位同学(两男两女)中选取2人主持活动,利用画树状图或表格法求恰为一男一女的概率.20. 如图,在平面直角坐标中, 的顶点坐标分别是 , , . (1)、将 以 为旋转中心旋转 ,画出旋转后对应的 ;(2)、将 平移后得到 ,若点 的对应点 的坐标为 ,求 的面积21. 2021年,州河边新建成了一座美丽的大桥.某学校数学兴趣小组组织了一次测桥墩高度的活动,如图,桥墩刚好在坡角为 的河床斜坡边,斜坡 长为48米,在点 处测得桥墩最高点 的仰角为 , 平行于水平线 , 长为 米,求桥墩 的高(结果保留1位小数).( , , , )
(1)、将 以 为旋转中心旋转 ,画出旋转后对应的 ;(2)、将 平移后得到 ,若点 的对应点 的坐标为 ,求 的面积21. 2021年,州河边新建成了一座美丽的大桥.某学校数学兴趣小组组织了一次测桥墩高度的活动,如图,桥墩刚好在坡角为 的河床斜坡边,斜坡 长为48米,在点 处测得桥墩最高点 的仰角为 , 平行于水平线 , 长为 米,求桥墩 的高(结果保留1位小数).( , , , )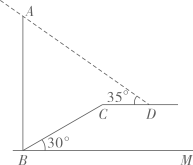
 22. 渠县是全国优质黄花主产地,某加工厂加工黄花的成本为30元/千克,根据市场调查发现,批发价定为48元/千克时,每天可销售500千克.为增大市场占有率,在保证盈利的情况下,工厂采取降价措施.批发价每千克降低1元,每天销量可增加50千克.(1)、写出工厂每天的利润 元与降价 元之间的函数关系.当降价2元时,工厂每天的利润为多少元?(2)、当降价多少元时,工厂每天的利润最大,最大为多少元?(3)、若工厂每天的利润要达到9750元,并让利于民,则定价应为多少元?23. 如图, 是 的直径, 为 上一点( 不与点 , 重合)连接 , ,过点 作 ,垂足为点 .将 沿 翻折,点 落在点 处得 , 交 于点 .
22. 渠县是全国优质黄花主产地,某加工厂加工黄花的成本为30元/千克,根据市场调查发现,批发价定为48元/千克时,每天可销售500千克.为增大市场占有率,在保证盈利的情况下,工厂采取降价措施.批发价每千克降低1元,每天销量可增加50千克.(1)、写出工厂每天的利润 元与降价 元之间的函数关系.当降价2元时,工厂每天的利润为多少元?(2)、当降价多少元时,工厂每天的利润最大,最大为多少元?(3)、若工厂每天的利润要达到9750元,并让利于民,则定价应为多少元?23. 如图, 是 的直径, 为 上一点( 不与点 , 重合)连接 , ,过点 作 ,垂足为点 .将 沿 翻折,点 落在点 处得 , 交 于点 .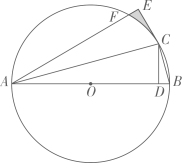 (1)、求证: 是 的切线;(2)、若 , ,求阴影部分面积.24. 某数学兴趣小组在数学课外活动中,对多边形内两要互相垂直的线段做了如下探究:
(1)、求证: 是 的切线;(2)、若 , ,求阴影部分面积.24. 某数学兴趣小组在数学课外活动中,对多边形内两要互相垂直的线段做了如下探究:(观察与猜想)
(1)、如图1,在正方形 中,点 , 分别是 , 上的两点,连接 , , ,则 的值为; (2)、如图2,在矩形 中, , ,点 是 上的一点,连接 , ,且 ,则 的值为;
(2)、如图2,在矩形 中, , ,点 是 上的一点,连接 , ,且 ,则 的值为;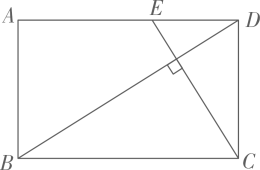 (3)、如图3,在四边形 中, ,点 为 上一点,连接 ,过点 作 的垂线交 的延长线于点 ,交 的延长线于点 ,求证: ;
(3)、如图3,在四边形 中, ,点 为 上一点,连接 ,过点 作 的垂线交 的延长线于点 ,交 的延长线于点 ,求证: ;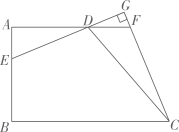 (4)、如图4,在 中, , , ,将 沿 翻折,点 落在点 处得 ,点 , 分别在边 , 上,连接 , ,且 .
(4)、如图4,在 中, , , ,将 沿 翻折,点 落在点 处得 ,点 , 分别在边 , 上,连接 , ,且 .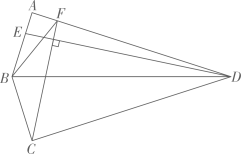
①求 的值;
②连接 ,若 ,直接写出 的长度.
25. 如图,在平面直角坐标系中,抛物线 交 轴于点 和 ,交 轴于点 ,抛物线的对称轴交 轴于点 ,交抛物线于点 .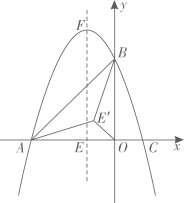 (1)、求抛物线的解析式;(2)、将线段 绕着点 沿顺时针方向旋转得到线段 ,旋转角为 ,连接 , ,求 的最小值.(3)、 为平面直角坐标系中一点,在抛物线上是否存在一点 ,使得以 , , , 为顶点的四边形为矩形?若存在,请直接写出点 的横坐标;若不存在,请说明理由;
(1)、求抛物线的解析式;(2)、将线段 绕着点 沿顺时针方向旋转得到线段 ,旋转角为 ,连接 , ,求 的最小值.(3)、 为平面直角坐标系中一点,在抛物线上是否存在一点 ,使得以 , , , 为顶点的四边形为矩形?若存在,请直接写出点 的横坐标;若不存在,请说明理由;