湖北省随州市2021年中考数学试卷
试卷更新日期:2021-06-25 类型:中考真卷
一、单选题
-
1. 2021的相反数是( )A、 -2021 B、2021 C、 D、2. 从今年公布的全国第七次人口普查数据可知,湖北省人口约为5700万,其中5700万用科学记数法可表示为( )A、 B、 C、 D、3. 如图,将一块含有 角的直角三角板放置在两条平行线上,若 ,则 为( )
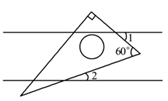 A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图是小明某一天测得的7次体温情况的折线统计图,下列信息不正确的是( )
A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图是小明某一天测得的7次体温情况的折线统计图,下列信息不正确的是( )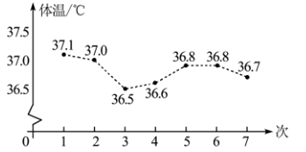 A、测得的最高体温为37.1℃ B、前3次测得的体温在下降 C、这组数据的众数是36.8 D、这组数据的中位数是36.66. 如图是由4个相同的小正方体构成的一个组合体,该组合体的三视图中完全相同的是( )
A、测得的最高体温为37.1℃ B、前3次测得的体温在下降 C、这组数据的众数是36.8 D、这组数据的中位数是36.66. 如图是由4个相同的小正方体构成的一个组合体,该组合体的三视图中完全相同的是( ) A、主视图和左视图 B、主视图和俯视图 C、左视图和俯视图 D、三个视图均相同7. 如图,从一个大正方形中截去面积为 和 的两个小正方形,若随机向大正方形内投一粒米,则米粒落在图中阴影部分的概率为( )
A、主视图和左视图 B、主视图和俯视图 C、左视图和俯视图 D、三个视图均相同7. 如图,从一个大正方形中截去面积为 和 的两个小正方形,若随机向大正方形内投一粒米,则米粒落在图中阴影部分的概率为( )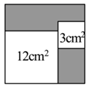 A、 B、 C、 D、8. 如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为 时,梯子顶端靠在墙面上的点 处,底端落在水平地面的点 处,现将梯子底端向墙面靠近,使梯子与地面所成角为 ,已知 ,则梯子顶端上升了( )
A、 B、 C、 D、8. 如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为 时,梯子顶端靠在墙面上的点 处,底端落在水平地面的点 处,现将梯子底端向墙面靠近,使梯子与地面所成角为 ,已知 ,则梯子顶端上升了( )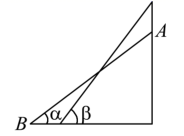 A、1米 B、1.5米 C、2米 D、2.5米9. 根据图中数字的规律,若第 个图中的 ,则 的值为( )
A、1米 B、1.5米 C、2米 D、2.5米9. 根据图中数字的规律,若第 个图中的 ,则 的值为( )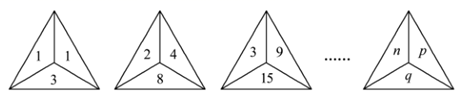 A、100 B、121 C、144 D、16910. 如图,已知抛物线 的对称轴在 轴右侧,抛物线与 轴交于点 和点 ,与 轴的负半轴交于点 ,且 ,则下列结论:① ;② ;③ ;④当 时,在 轴下方的抛物线上一定存在关于对称轴对称的两点 , (点 在点 左边),使得 .其中正确的有( )
A、100 B、121 C、144 D、16910. 如图,已知抛物线 的对称轴在 轴右侧,抛物线与 轴交于点 和点 ,与 轴的负半轴交于点 ,且 ,则下列结论:① ;② ;③ ;④当 时,在 轴下方的抛物线上一定存在关于对称轴对称的两点 , (点 在点 左边),使得 .其中正确的有( )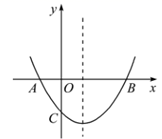 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
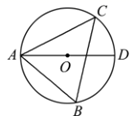
11. 计算: .12. 如图, 是 的外接圆,连接 并延长交 于点 ,若 ,则 的度数为.
 13. 已知关于 的方程 ( )的两实数根为 , ,若 ,则 .14. 如图,在 中, , , ,将 绕点 逆时针旋转角 ( )得到 ,并使点 落在 边上,则点 所经过的路径长为.(结果保留 )
13. 已知关于 的方程 ( )的两实数根为 , ,若 ,则 .14. 如图,在 中, , , ,将 绕点 逆时针旋转角 ( )得到 ,并使点 落在 边上,则点 所经过的路径长为.(结果保留 )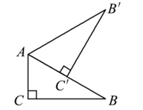 15. 2021年5月7日,《科学》杂志发布了我国成功研制出可编程超导量子计算机“祖冲之”号的相关研究成果.祖冲之是我国南北朝时期杰出的数学家,他是第一个将圆周率 精确到小数点后第七位的人,他给出 的两个分数形式: (约率)和 (密率).同时期数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法,其理论依据是:设实数 的不足近似值和过剩近似值分别为 和 (即有 ,其中 , , , 为正整数),则 是 的更为精确的近似值.例如:已知 ,则利用一次“调日法”后可得到 的一个更为精确的近似分数为: ;由于 ,再由 ,可以再次使用“调日法”得到 的更为精确的近似分数……现已知 ,则使用两次“调日法”可得到 的近似分数为.16. 如图,在 中, , 为 的中点, 平分 交 于点 , , 分别与 , 交于点 , ,连接 , ,则 的值为;若 ,则 的值为.
15. 2021年5月7日,《科学》杂志发布了我国成功研制出可编程超导量子计算机“祖冲之”号的相关研究成果.祖冲之是我国南北朝时期杰出的数学家,他是第一个将圆周率 精确到小数点后第七位的人,他给出 的两个分数形式: (约率)和 (密率).同时期数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法,其理论依据是:设实数 的不足近似值和过剩近似值分别为 和 (即有 ,其中 , , , 为正整数),则 是 的更为精确的近似值.例如:已知 ,则利用一次“调日法”后可得到 的一个更为精确的近似分数为: ;由于 ,再由 ,可以再次使用“调日法”得到 的更为精确的近似分数……现已知 ,则使用两次“调日法”可得到 的近似分数为.16. 如图,在 中, , 为 的中点, 平分 交 于点 , , 分别与 , 交于点 , ,连接 , ,则 的值为;若 ,则 的值为.
三、解答题
-
17. 先化简,再求值: ,其中 .18. 如图,在菱形 中, , 是对角线 上的两点,且 .
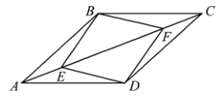 (1)、求证: ≌ ;(2)、证明四边形 是菱形.19. 疫苗接种初期,为更好地响应国家对符合条件的人群接种新冠疫苗的号召,某市教育部门随机抽取了该市部分七、八、九年级教师,了解教师的疫苗接种情况,得到如下统计表:
(1)、求证: ≌ ;(2)、证明四边形 是菱形.19. 疫苗接种初期,为更好地响应国家对符合条件的人群接种新冠疫苗的号召,某市教育部门随机抽取了该市部分七、八、九年级教师,了解教师的疫苗接种情况,得到如下统计表:已接种
未接种
合计
七年级
30
10
40
八年级
35
15
九年级
40
60
合计
105
150
(1)、表中, , , ;(2)、由表中数据可知,统计的教师中接种率最高的是年级教师;(填“七”或“八”或“九”)(3)、若该市初中七、八、九年级一共约有8000名教师,根据抽样结果估计未接种的教师约有人;(4)、为更好地响应号召,立德中学从最初接种的4名教师(其中七年级1名,八年级1名,九年级2名)中随机选取2名教师谈谈接种的感受,请用列表或画树状图的方法,求选中的两名教师恰好不在同一年级的概率.20. 如图,一次函数 的图象与 轴、 轴分别交于点 , ,与反比例函数 ( )的图象交于点 , .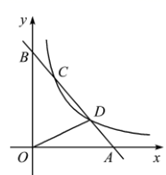 (1)、分别求出两个函数的解析式;(2)、连接 ,求 的面积.21. 如图, 是以 为直径的 上一点,过点 的切线 交 的延长线于点 ,过点 作 交 的延长线于点 ,垂足为点 .
(1)、分别求出两个函数的解析式;(2)、连接 ,求 的面积.21. 如图, 是以 为直径的 上一点,过点 的切线 交 的延长线于点 ,过点 作 交 的延长线于点 ,垂足为点 .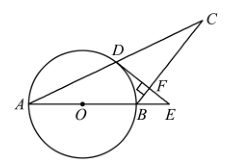 (1)、求证: ;(2)、若 的直径 为9, .
(1)、求证: ;(2)、若 的直径 为9, .①求线段 的长;
②求线段 的长.
22. 如今我国的大棚(如图1)种植技术已十分成熟.小明家的菜地上有一个长为16米的蔬菜大棚,其横截面顶部为抛物线型,大棚的一端固定在离地面高1米的墙体 处,另一端固定在离地面高2米的墙体 处,现对其横截面建立如图2所示的平面直角坐标系.已知大棚上某处离地面的高度 (米)与其离墙体 的水平距离 (米)之间的关系满足 ,现测得 , 两墙体之间的水平距离为6米.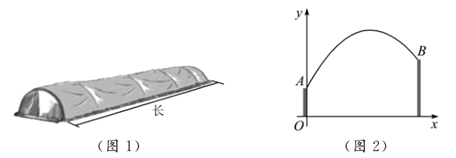 (1)、直接写出 , 的值;(2)、求大棚的最高处到地面的距离;(3)、小明的爸爸欲在大棚内种植黄瓜,需搭建高为 米的竹竿支架若干,已知大棚内可以搭建支架的土地平均每平方米需要4根竹竿,则共需要准备多少根竹竿?23. 等面积法是一种常用的、重要的数学解题方法.它是利用“同一个图形的面积相等”、“分割图形后各部分的面积之和等于原图形的面积”、“同底等高或等底同高的两个三角形面积相等”等性质解决有关数学问题,在解题中,灵活运用等面积法解决相关问题,可以使解题思路清晰,解题过程简便快捷.
(1)、直接写出 , 的值;(2)、求大棚的最高处到地面的距离;(3)、小明的爸爸欲在大棚内种植黄瓜,需搭建高为 米的竹竿支架若干,已知大棚内可以搭建支架的土地平均每平方米需要4根竹竿,则共需要准备多少根竹竿?23. 等面积法是一种常用的、重要的数学解题方法.它是利用“同一个图形的面积相等”、“分割图形后各部分的面积之和等于原图形的面积”、“同底等高或等底同高的两个三角形面积相等”等性质解决有关数学问题,在解题中,灵活运用等面积法解决相关问题,可以使解题思路清晰,解题过程简便快捷.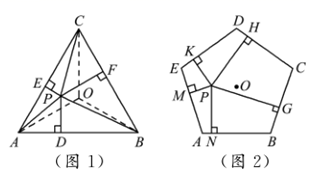
 (1)、在直角三角形中,两直角边长分别为3和4,则该直角三角形斜边上的高的长为 , 其内切圆的半径长为;(2)、①如图1, 是边长为 的正 内任意一点,点 为 的中心,设点 到 各边距离分别为 , , ,连接 , , ,由等面积法,易知 ,可得 ▲ ;(结果用含 的式子表示)
(1)、在直角三角形中,两直角边长分别为3和4,则该直角三角形斜边上的高的长为 , 其内切圆的半径长为;(2)、①如图1, 是边长为 的正 内任意一点,点 为 的中心,设点 到 各边距离分别为 , , ,连接 , , ,由等面积法,易知 ,可得 ▲ ;(结果用含 的式子表示)②如图2, 是边长为 的正五边形 内任意一点,设点 到五边形 各边距离分别为 , , , , ,参照①的探索过程,试用含 的式子表示 的值.(参考数据: , )
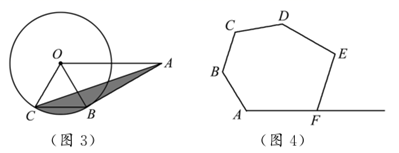
(3)、①如图3,已知 的半径为2,点 为 外一点, , 切 于点 ,弦 ,连接 ,则图中阴影部分的面积为 ▲ ;(结果保留 )②如图4,现有六边形花坛 ,由于修路等原因需将花坛进行改造.若要将花坛形状改造成五边形 ,其中点 在 的延长线上,且要保证改造前后花坛的面积不变,试确定点 的位置,并说明理由.
24. 在平面直角坐标系中,抛物线 与 轴交于点 和点 ,与 轴交于点 ,顶点 的坐标为 . (1)、直接写出抛物线的解析式;(2)、如图1,若点 在抛物线上且满足 ,求点 的坐标;(3)、如图2, 是直线 上一个动点,过点 作 轴交抛物线于点 , 是直线 上一个动点,当 为等腰直角三角形时,直接写出此时点 及其对应点 的坐标
(1)、直接写出抛物线的解析式;(2)、如图1,若点 在抛物线上且满足 ,求点 的坐标;(3)、如图2, 是直线 上一个动点,过点 作 轴交抛物线于点 , 是直线 上一个动点,当 为等腰直角三角形时,直接写出此时点 及其对应点 的坐标