湖北省恩施市2021年中考数学试卷
试卷更新日期:2021-06-25 类型:中考真卷
一、单选题
-
1. -6的相反数是( )A、-6 B、6 C、±6 D、2. 全国第七次人口普查湖北省常住人口约为5780万,将数5780 万用科学记数法表示为( )A、 B、 C、 D、3. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、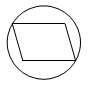 4. 图中几何体的俯视图是( )
4. 图中几何体的俯视图是( ) A、
A、 B、
B、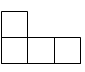 C、
C、 D、
D、 5. 下列运算正确的是( )A、 B、 C、 D、6. 工厂从三名男工人和两名女工人中,选出两人参加技能大赛,则这两名工人恰好都是男工人的概率为( )A、 B、 C、 D、7. 从 , , 这三个实数中任选两数相乘,所有积中小于2的有( )个.A、0 B、1 C、2 D、38. 分式方程 的解是( )A、 B、 C、 D、9. 某物体在力 的作用下,沿力的方向移动的距离为 ,力对物体所做的功 与 的对应关系如图所示,则下列结论正确的是( )
5. 下列运算正确的是( )A、 B、 C、 D、6. 工厂从三名男工人和两名女工人中,选出两人参加技能大赛,则这两名工人恰好都是男工人的概率为( )A、 B、 C、 D、7. 从 , , 这三个实数中任选两数相乘,所有积中小于2的有( )个.A、0 B、1 C、2 D、38. 分式方程 的解是( )A、 B、 C、 D、9. 某物体在力 的作用下,沿力的方向移动的距离为 ,力对物体所做的功 与 的对应关系如图所示,则下列结论正确的是( ) A、 B、 C、 D、10. 如图,在 中, , , ,则 的面积为( )
A、 B、 C、 D、10. 如图,在 中, , , ,则 的面积为( ) A、30 B、60 C、65 D、11. 如图,在 的正方形网格中,每个小正方形的边长都为1, 为 与正方形网格线的交点,下列结论正确的是( )
A、30 B、60 C、65 D、11. 如图,在 的正方形网格中,每个小正方形的边长都为1, 为 与正方形网格线的交点,下列结论正确的是( ) A、 B、 C、 D、12. 如图,已知二次函数 的图象与 轴交于 ,顶点是 ,则以下结论:① ;② ;③若 ,则 或 ;④ .其中正确的有( )个.
A、 B、 C、 D、12. 如图,已知二次函数 的图象与 轴交于 ,顶点是 ,则以下结论:① ;② ;③若 ,则 或 ;④ .其中正确的有( )个.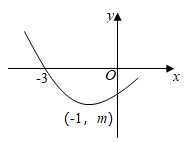 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 分解因式: .14. 如图,已知 , , ,则 .
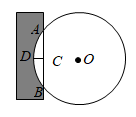
 15. 《九章算术》被尊为古代数学“群经之首”,其卷九勾股篇记载:今有圆材埋于壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?如图,大意是,今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深 等于1寸,锯道 长1尺,问圆形木材的直径是多少?(1尺=10寸)
15. 《九章算术》被尊为古代数学“群经之首”,其卷九勾股篇记载:今有圆材埋于壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?如图,大意是,今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深 等于1寸,锯道 长1尺,问圆形木材的直径是多少?(1尺=10寸)答:圆形木材的直径寸;
 16. 古希腊数学家定义了五边形数,如下表所示,将点按照表中方式排列成五边形点阵,图形中的点的个数即五边形数;
16. 古希腊数学家定义了五边形数,如下表所示,将点按照表中方式排列成五边形点阵,图形中的点的个数即五边形数;图形






…
五边形数
1
5
12
22
35
51
…
将五边形数1,5,12,22,35,51,…,排成如下数表;
1 第一行
5 12 第二行
22 35 51 第三行
… … … … …
观察这个数表,则这个数表中的第八行从左至右第2个数为.
三、解答题
-
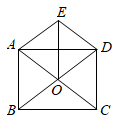
17. 先化简,再求值: ,其中 .18. 如图,矩形 的对角线 , 交于点 ,且 , ,连接 .求证: .
 19. 九(1)班准备从甲、乙两名男生中选派一名参加学校组织的一分钟跳绳比赛,在相同的条件下,分别对两名男生进行了八次一分钟跳绳测试.现将测试结果绘制成如下不完整的统计图表,请根据统计图表中的信息解答下列问题:
19. 九(1)班准备从甲、乙两名男生中选派一名参加学校组织的一分钟跳绳比赛,在相同的条件下,分别对两名男生进行了八次一分钟跳绳测试.现将测试结果绘制成如下不完整的统计图表,请根据统计图表中的信息解答下列问题:平均数
中位数
众数
方差
甲
175
93.75
乙
175
175
180,175,170
 (1)、求 、 的值;(2)、若九(1)班选一位成绩稳定的选手参赛,你认为应选谁,请说明理由;(3)、根据以上的数据分析,请你运用所学统计知识,任选两个角度评价甲乙两名男生一分钟跳绳成绩谁优.20. 乡村振兴使人民有更舒适的居住条件,更优美的生活环境,如图是怡佳新村中的两栋居民楼,小明在甲居民楼的楼顶 处观测乙居民楼楼底 处的俯角是 ,观测乙居民楼楼顶 处的仰角为 ,已知甲居民楼的高为 ,求乙居民楼的高.(参考数据: , ,结果精确到 )
(1)、求 、 的值;(2)、若九(1)班选一位成绩稳定的选手参赛,你认为应选谁,请说明理由;(3)、根据以上的数据分析,请你运用所学统计知识,任选两个角度评价甲乙两名男生一分钟跳绳成绩谁优.20. 乡村振兴使人民有更舒适的居住条件,更优美的生活环境,如图是怡佳新村中的两栋居民楼,小明在甲居民楼的楼顶 处观测乙居民楼楼底 处的俯角是 ,观测乙居民楼楼顶 处的仰角为 ,已知甲居民楼的高为 ,求乙居民楼的高.(参考数据: , ,结果精确到 )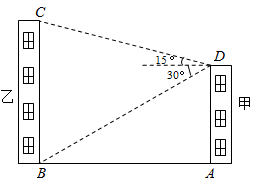 21. 如图,在平面直角坐标系中, 的斜边 在 轴上,坐标原点是 的中点, , ,双曲线 经过点 .
21. 如图,在平面直角坐标系中, 的斜边 在 轴上,坐标原点是 的中点, , ,双曲线 经过点 . (1)、求 ;(2)、直线 与双曲线 在第四象限交于点 .求 的面积.22. “互联网+”让我国经济更具活力,直播助销就是运用“互联网+”的生机勃勃的销售方式,让大山深处的农产品远销全国各地.甲为当地特色花生与茶叶两种产品助销.已知每千克花生的售价比每千克茶叶的售价低40元,销售50千克花生与销售10千克茶叶的总售价相同.(1)、求每千克花生、茶叶的售价;(2)、已知花生的成本为6元/千克,茶叶的成本为36元/千克.甲计划两种产品共助销60千克,总成本不高于1260元,且花生的数量不高于茶叶数量的2倍.则花生、茶叶各销售多少千克可获得最大利润?最大利润是多少?23. 如图,在 中, , 与 相交于点 ,与 相交于点 ,连接 ,已知 .
(1)、求 ;(2)、直线 与双曲线 在第四象限交于点 .求 的面积.22. “互联网+”让我国经济更具活力,直播助销就是运用“互联网+”的生机勃勃的销售方式,让大山深处的农产品远销全国各地.甲为当地特色花生与茶叶两种产品助销.已知每千克花生的售价比每千克茶叶的售价低40元,销售50千克花生与销售10千克茶叶的总售价相同.(1)、求每千克花生、茶叶的售价;(2)、已知花生的成本为6元/千克,茶叶的成本为36元/千克.甲计划两种产品共助销60千克,总成本不高于1260元,且花生的数量不高于茶叶数量的2倍.则花生、茶叶各销售多少千克可获得最大利润?最大利润是多少?23. 如图,在 中, , 与 相交于点 ,与 相交于点 ,连接 ,已知 . (1)、求证: 为 的切线;(2)、若 , ,求 的长.24. 如图,在平面直角坐标系中,四边形 为正方形,点 , 在 轴上,抛物线 经过点 , 两点,且与直线 交于另一点 .
(1)、求证: 为 的切线;(2)、若 , ,求 的长.24. 如图,在平面直角坐标系中,四边形 为正方形,点 , 在 轴上,抛物线 经过点 , 两点,且与直线 交于另一点 . (1)、求抛物线的解析式;(2)、 为抛物线对称轴上一点, 为平面直角坐标系中的一点,是否存在以点 , , , 为顶点的四边形是以 为边的菱形.若存在,请求出点 的坐标;若不存在,请说明理由;(3)、 为 轴上一点,过点 作抛物线对称轴的垂线,垂足为 ,连接 , .探究 是否存在最小值.若存在,请求出这个最小值及点 的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、 为抛物线对称轴上一点, 为平面直角坐标系中的一点,是否存在以点 , , , 为顶点的四边形是以 为边的菱形.若存在,请求出点 的坐标;若不存在,请说明理由;(3)、 为 轴上一点,过点 作抛物线对称轴的垂线,垂足为 ,连接 , .探究 是否存在最小值.若存在,请求出这个最小值及点 的坐标;若不存在,请说明理由.