四川省绵阳市梓潼县2021年数学中考二诊试卷
试卷更新日期:2021-06-25 类型:中考模拟
一、单选题
-
1. 计算|﹣1|﹣3,结果正确的是( )A、﹣4 B、﹣3 C、﹣2 D、﹣12. 太阳半径约6960000000,其中数据696000000用科学记数法表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 某班级开展“好书伴成长”读书活动,统计了1至7月份该班同学每月阅读课外书的数量,绘制了折线统计图,下列说法正确的是( )
 A、每月阅读课外书本数的众数是45 B、每月阅读课外书本数的中位数是58 C、从2到6月份阅读课外书的本数逐月下降 D、从1到7月份每月阅读课外书本数的最大值比最小值多455. 如图,直线 ,点A在直线 上,以点A为圆心,适当长度为半径画弧,分别交直线 、 于B、C两点,连结AC、BC.若 ,则 的大小为( )
A、每月阅读课外书本数的众数是45 B、每月阅读课外书本数的中位数是58 C、从2到6月份阅读课外书的本数逐月下降 D、从1到7月份每月阅读课外书本数的最大值比最小值多455. 如图,直线 ,点A在直线 上,以点A为圆心,适当长度为半径画弧,分别交直线 、 于B、C两点,连结AC、BC.若 ,则 的大小为( )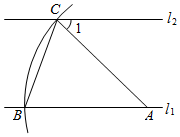 A、 B、 C、 D、6. 随着全球能源危机的逐渐加重,太阳能发电行业发展迅速全球太阳能光伏应用市场持续稳步增长,2019年全球装机总量约600GW,预计到2021年全球装机总量达到864GW.设全球新增装机量的年平均增长率为x,则x值为( )A、20% B、30% C、40% D、50%7. 不等式组 的解集是 ,那么m的取值范围是( )A、 B、 C、 D、8. 如图,在 中, , , ,则 的度数为( )
A、 B、 C、 D、6. 随着全球能源危机的逐渐加重,太阳能发电行业发展迅速全球太阳能光伏应用市场持续稳步增长,2019年全球装机总量约600GW,预计到2021年全球装机总量达到864GW.设全球新增装机量的年平均增长率为x,则x值为( )A、20% B、30% C、40% D、50%7. 不等式组 的解集是 ,那么m的取值范围是( )A、 B、 C、 D、8. 如图,在 中, , , ,则 的度数为( )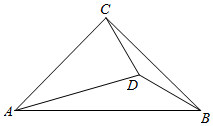 A、12° B、13° C、14° D、15°9. 如图所示的图形中,每个三角形上各有一个数字,若六个三角形上的数字之和为20,则称该图形是“和谐图形”.已知其中四个三角形上的数字之和为14,现从1,2,3,4,5中任取两个数字标在另外两个三角形上,则恰好使该图形为“和谐图形”的概率为( )
A、12° B、13° C、14° D、15°9. 如图所示的图形中,每个三角形上各有一个数字,若六个三角形上的数字之和为20,则称该图形是“和谐图形”.已知其中四个三角形上的数字之和为14,现从1,2,3,4,5中任取两个数字标在另外两个三角形上,则恰好使该图形为“和谐图形”的概率为( ) A、 B、 C、 D、10. 如图,在Rt△ABC中,∠ACB=90°,AC=BC,过点C作CD⊥AB,垂足为D,点E为BC的中点,AE与CD交于点F,若DF的长为 ,则AE的长为( )
A、 B、 C、 D、10. 如图,在Rt△ABC中,∠ACB=90°,AC=BC,过点C作CD⊥AB,垂足为D,点E为BC的中点,AE与CD交于点F,若DF的长为 ,则AE的长为( )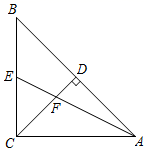 A、 B、2 C、 D、211. 如图,抛物线y=ax2+bx+c经过(﹣1,0)和(0,﹣1)两点,则抛物线y=cx2+bx+a的图象大致为( )
A、 B、2 C、 D、211. 如图,抛物线y=ax2+bx+c经过(﹣1,0)和(0,﹣1)两点,则抛物线y=cx2+bx+a的图象大致为( )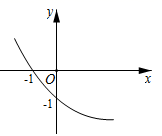 A、
A、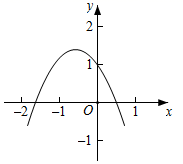 B、
B、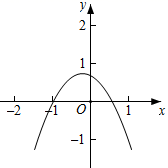 C、
C、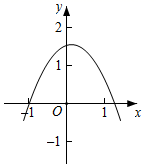 D、
D、 12. 如图,有一张矩形纸条 , , ,点 , 分别在边 , 上, .现将四边形 沿 折叠,使点 , 分别落在点 , 上.在点 从点 运动到点 的过程中,若边 与边 交于点 ,则点 相应运动的路径长为( )
12. 如图,有一张矩形纸条 , , ,点 , 分别在边 , 上, .现将四边形 沿 折叠,使点 , 分别落在点 , 上.在点 从点 运动到点 的过程中,若边 与边 交于点 ,则点 相应运动的路径长为( )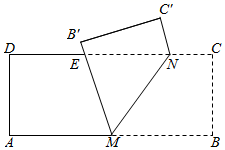 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 把多项式 分解因式的结果是 .14. 将抛物线 向上平移3个单位长度后,经过点 ,则 的值是 .15. 无盖圆柱形杯子的展开图如图所示.将一根长为20cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有cm.
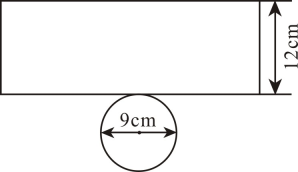 16. 关于x的方程 的解是正数,则a的取值范围是.17. 如图,在 中, ,点 分别在 上,且 ,点 分别为 的中点,则 的长为 .
16. 关于x的方程 的解是正数,则a的取值范围是.17. 如图,在 中, ,点 分别在 上,且 ,点 分别为 的中点,则 的长为 .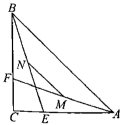 18. 如图,在矩形 , , , 为线段 上的一动点,且和 , 不重合,连接 ,过点 作 交 于 ,将 沿 翻折到平面内,使点 恰好落在 边上的点 ,则 长为.
18. 如图,在矩形 , , , 为线段 上的一动点,且和 , 不重合,连接 ,过点 作 交 于 ,将 沿 翻折到平面内,使点 恰好落在 边上的点 ,则 长为.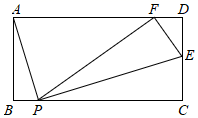
三、解答题
-
19.(1)、计算: .(2)、先化简,再求值: ,其中 满足 .20. 新冠肺炎疫情期间,我市对学生进行了“停课不停学”的线上教学活动.某中学为了解这期间九年级学生数学学习的情况,开学后进行了两次诊断性练习.综合成绩由两次练习成绩组成,其中第一次练习成绩占40%,第二次练习成绩占60%.当综合成绩不低于135分时,该生数学学科综合评价为优秀.(1)、小明同学的两次练习成绩之和为260分,综合成绩为132分,则他这两次练习成绩各得多少分?(2)、如果小张同学第一次练习成绩为120分,综合成绩要达到优秀,他的第二次练习成绩至少要得多少分?21. 珠海市有A,B,C,D,E五个景区很受游客喜爱.对某小区居民在暑假期间去以上五个景区旅游(只选一个景区)的意向做了一次随机调查统计,并根据这个统计结果制作了如下两幅不完整的统计图.
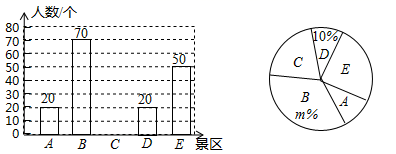 (1)、该小区居民在这次随机调查中被调查到的人数是人,m=;(2)、若该小区有居民1500人,试估计去C景区旅游的居民约有多少人?(3)、甲、乙两人暑假打算游玩,甲从B、C两个景点中任意选择一个游玩,乙从B、C 、E三个景点中任意选择一个游玩.求甲、乙恰好游玩同一景点的概率.22. 如图,在平面直角坐标系中,菱形OBCD的边OB在x轴上,反比例函数y= (x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).
(1)、该小区居民在这次随机调查中被调查到的人数是人,m=;(2)、若该小区有居民1500人,试估计去C景区旅游的居民约有多少人?(3)、甲、乙两人暑假打算游玩,甲从B、C两个景点中任意选择一个游玩,乙从B、C 、E三个景点中任意选择一个游玩.求甲、乙恰好游玩同一景点的概率.22. 如图,在平面直角坐标系中,菱形OBCD的边OB在x轴上,反比例函数y= (x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).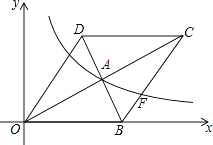 (1)、求反比例函数的表达式;(2)、求点F的坐标.23. 如图, 是⊙O的直径, 是⊙O的弦, 交 于点 ,连接 , .过点 作 ,垂足为 , .
(1)、求反比例函数的表达式;(2)、求点F的坐标.23. 如图, 是⊙O的直径, 是⊙O的弦, 交 于点 ,连接 , .过点 作 ,垂足为 , .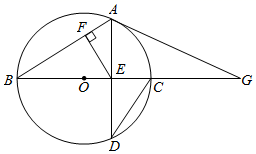 (1)、求证: ;(2)、点 在 的延长线上,连接 , .
(1)、求证: ;(2)、点 在 的延长线上,连接 , .①求证: 与⊙O相切;
②当 , 时,求 的长.
24. 在正方形 中,动点 , 分别从 , 两点同时出发,以相同的速度在直线 , 上移动.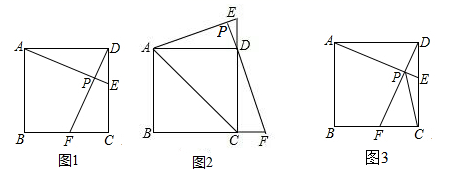 (1)、如图1,当点 在边 上自 向 移动,同时点 在边 上自 向 移动时,连接 和 交于点 ,请你直接写出 与 的关系.(2)、如图2,当 , 分别在边 , 的延长线上移动时,连接 , , ,当 为等腰三角形时,求 的值.(3)、如图3,当点 在边 上自 向 移动,同时点 在边 上自 向 移动时,连接 和 交于点 ,由于点 , 的移动,使得点 也随之运动.若 ,求线段 的最小值.25. 如图1,已知抛物线 与 轴交于 、 两点,与 轴交于点 .
(1)、如图1,当点 在边 上自 向 移动,同时点 在边 上自 向 移动时,连接 和 交于点 ,请你直接写出 与 的关系.(2)、如图2,当 , 分别在边 , 的延长线上移动时,连接 , , ,当 为等腰三角形时,求 的值.(3)、如图3,当点 在边 上自 向 移动,同时点 在边 上自 向 移动时,连接 和 交于点 ,由于点 , 的移动,使得点 也随之运动.若 ,求线段 的最小值.25. 如图1,已知抛物线 与 轴交于 、 两点,与 轴交于点 .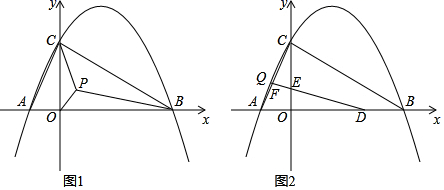 (1)、写出 , , 三点的坐标.(2)、若点 为 内一点,求 的最小值.(3)、如图2,点 为对称轴左侧抛物线上一动点,点 ,直线 分别与 轴、直线 交于 , 两点,当 为等腰三角形时,请求出 的长.
(1)、写出 , , 三点的坐标.(2)、若点 为 内一点,求 的最小值.(3)、如图2,点 为对称轴左侧抛物线上一动点,点 ,直线 分别与 轴、直线 交于 , 两点,当 为等腰三角形时,请求出 的长.