四川省绵阳市三台县2021年数学中考二诊试卷
试卷更新日期:2021-06-25 类型:中考模拟
一、单选题
-
1. 下图是用来证明勾股定理的图案被称为“赵爽弦图”,由四个全等的直角三角形和一个小正方形拼成的大正方形,对其对称性表述,正确的是( )
 A、轴对称图形 B、中心对称图形 C、既是轴对称图形又是中心对称图形 D、既不是轴对称图形又不是中心对称图形2. 2020年初,新冠肺炎疫情袭卷全球,截止2020年底,据不完全统计,全球累计确诊人数约为8096万人,用科学记数法表示为( )A、 B、 C、 D、3. 下列运算中正确的有( )
A、轴对称图形 B、中心对称图形 C、既是轴对称图形又是中心对称图形 D、既不是轴对称图形又不是中心对称图形2. 2020年初,新冠肺炎疫情袭卷全球,截止2020年底,据不完全统计,全球累计确诊人数约为8096万人,用科学记数法表示为( )A、 B、 C、 D、3. 下列运算中正确的有( )① ;② ;③ ;④
A、1个 B、2个 C、3个 D、4个4. 如图所示的几何体,它的俯视图是( )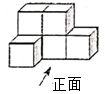 A、
A、 B、
B、 C、
C、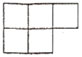 D、
D、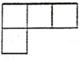 5. 下列二次根式中,无论x取什么值都有意义的是( )A、 B、 C、 D、6. 小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图(1);小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图(2)那样的正方形,中间还留下了一个洞,恰好是面积为4cm2的小正方形,则每个小长方形的面积为( )
5. 下列二次根式中,无论x取什么值都有意义的是( )A、 B、 C、 D、6. 小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图(1);小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图(2)那样的正方形,中间还留下了一个洞,恰好是面积为4cm2的小正方形,则每个小长方形的面积为( ) A、135cm2 B、108cm2 C、68cm2 D、60cm27. 有一首《对子歌》中唱到:天对地,雨对风,大陆对长空.现将“天,雨,大,空”四个字书写在材质、大小完全相同的卡片上,在暗箱搅匀后,随机抽取两张,恰为“天”、“空”二字的概率为( )A、 B、 C、 D、8. 实数 的平方根分别是 和 ,且 ,则不等式 的解集为( )A、 B、 C、 D、9. “垃圾分类做得好,明天生活会更好”,学校需要购买分类垃圾桶10个,放在校园的公共区域,市场上有A型和B型两种分类垃圾桶,A型分类垃圾桶350元/个,B型分类垃圾桶400元/个,总费用不超过3650元,则不同的购买方式有( )A、2种 B、3种 C、4种 D、5种10. 在 中,已知 , , .如图所示,将 绕点 按逆时针方向旋转 后得到 .则图中阴影部分面积为( )
A、135cm2 B、108cm2 C、68cm2 D、60cm27. 有一首《对子歌》中唱到:天对地,雨对风,大陆对长空.现将“天,雨,大,空”四个字书写在材质、大小完全相同的卡片上,在暗箱搅匀后,随机抽取两张,恰为“天”、“空”二字的概率为( )A、 B、 C、 D、8. 实数 的平方根分别是 和 ,且 ,则不等式 的解集为( )A、 B、 C、 D、9. “垃圾分类做得好,明天生活会更好”,学校需要购买分类垃圾桶10个,放在校园的公共区域,市场上有A型和B型两种分类垃圾桶,A型分类垃圾桶350元/个,B型分类垃圾桶400元/个,总费用不超过3650元,则不同的购买方式有( )A、2种 B、3种 C、4种 D、5种10. 在 中,已知 , , .如图所示,将 绕点 按逆时针方向旋转 后得到 .则图中阴影部分面积为( ) A、 B、 C、 D、11. 如图, 和 是等腰直角三角形, , , 的顶点 在 的斜边上,若 , ,连接 交 于点 ,则下列说法:① , , , 四点在同一圆上;② ;③ ;④图中有相似三角形共有4对;⑤ ,正确的个数为( )
A、 B、 C、 D、11. 如图, 和 是等腰直角三角形, , , 的顶点 在 的斜边上,若 , ,连接 交 于点 ,则下列说法:① , , , 四点在同一圆上;② ;③ ;④图中有相似三角形共有4对;⑤ ,正确的个数为( )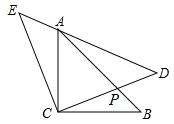 A、2个 B、3个 C、4个 D、5个12. 如图,在平面直角坐标系中,直线 与双曲线 交于 、 两点, 是以点 为圆心,半径长 的圆上一动点,连结 , 为 的中点.若线段 长度的最大值为2,则 的值为( )
A、2个 B、3个 C、4个 D、5个12. 如图,在平面直角坐标系中,直线 与双曲线 交于 、 两点, 是以点 为圆心,半径长 的圆上一动点,连结 , 为 的中点.若线段 长度的最大值为2,则 的值为( ) A、 B、 C、-2 D、
A、 B、 C、-2 D、二、填空题
-
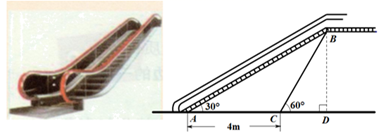
13. 因式分解: .14. 如图是某商场营业大厅自动扶梯示意图.自动扶梯 的倾斜角为 ,在自动扶梯下方地面 处测得扶梯顶端 的仰角为 , 、 之间的距离为4 . 则自动扶梯的垂直高度 = .(结果保留根号)
 15. 已知实数 满足 ,那么 的值为.16. 在△ABC中,AB=15 cm,AC=13 cm,BC边上的高为12 cm,则△ABC的面积为 .17. 如图,有一块直角三角形土地,它两条直边 米, 米,某单位要沿着斜边 修一座底面是矩形 的大楼, 、 分别在边 、 上,这个矩形 的面积最大值是.
15. 已知实数 满足 ,那么 的值为.16. 在△ABC中,AB=15 cm,AC=13 cm,BC边上的高为12 cm,则△ABC的面积为 .17. 如图,有一块直角三角形土地,它两条直边 米, 米,某单位要沿着斜边 修一座底面是矩形 的大楼, 、 分别在边 、 上,这个矩形 的面积最大值是.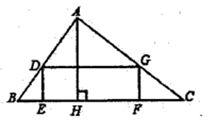 18. 如图,在正方形 中, , 与 交于点 , 是 的中点,点 在 边上,且 . 为对角线 上一点,则 的最大值为.
18. 如图,在正方形 中, , 与 交于点 , 是 的中点,点 在 边上,且 . 为对角线 上一点,则 的最大值为.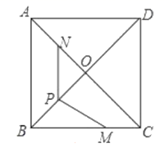
三、解答题
-
19.(1)、计算: .(2)、先化简,再求值: ,其中 .20. 某学校七年级、八年级各有500名学生,为了解两个年级的学生对垃圾分类知识的掌握情况,学校从七年级、八年级各随机抽取20名学生进行垃圾分类知识测试,满分100分,成绩整理分析过程如下,请补充完整:
(收集数据)七年级20名学生测试成绩统计如下:
67,58,64,56,69,70,95,84,74,77,78,78,71,86,91,86,86,92,86,70
(整理数据)按照如下分数段整理、描述两组样本数据:
成绩
七年级
2
3
7
5
3
八年级
0
4
5
7
4
(分析数据)两组样本数据的平均数、中位数、众数、方差如下表所示:
年级
平均数
中位数
众数
方差
七年级
76.9
126.2
八年级
79.2
81
74
100.4
(1)、请直接写出 , 的值;(2)、根据抽样调查数据,估计七年级垃圾分类知识测试成绩在80分及其以上的大约有多少人?(3)、通过以上分析,你认为哪个年级对垃圾分类知识掌握得更好,并说明推断的合理性(说明两条理由即可).21. 如图,一次函数 的图象与反比例函数 的图象交于点 、 两点,与 轴、 轴分别交于 、 两点,且点 的坐标为 .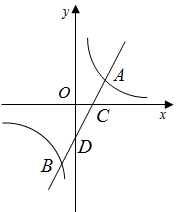 (1)、求一次函数和反比例函数的表达式.(2)、求 的面积.(3)、点 为反比例函数图象上的一个动点, 轴于 ,是否存在以 、 、 为顶点的三角形与 相似,若存在,直接写出 点的坐标,若不存在,请说明理由.22. 如图,已知 , , 为 的直径,斜边 交 于点 , 平分 , 于点 , 的延长线与 交于点 .
(1)、求一次函数和反比例函数的表达式.(2)、求 的面积.(3)、点 为反比例函数图象上的一个动点, 轴于 ,是否存在以 、 、 为顶点的三角形与 相似,若存在,直接写出 点的坐标,若不存在,请说明理由.22. 如图,已知 , , 为 的直径,斜边 交 于点 , 平分 , 于点 , 的延长线与 交于点 .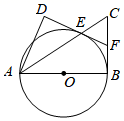 (1)、求证: 是 切线;(2)、求证: ;(3)、若 , ,求 的长.23. 小明投资销售一种进价为每件20元的护眼台灯.经过市场调研发现,每月销售的数量y(件)是售价x(元/件)的一次函数,其对应关系如表:
(1)、求证: 是 切线;(2)、求证: ;(3)、若 , ,求 的长.23. 小明投资销售一种进价为每件20元的护眼台灯.经过市场调研发现,每月销售的数量y(件)是售价x(元/件)的一次函数,其对应关系如表:x/(元/件)
22
25
30
35
…
y/件
280
250
200
150
…
在销售过程中销售单价不低于成本价,物价局规定每件商品的利润不得高于成本价的60%,
(1)、请求出y关于x的函数关系式.(2)、设小明每月获得利润为w(元),求每月获得利润w(元)与售价x(元/件)之间的函数关系式,并确定自变量x的取值范围.(3)、当售价定为多少元/件时,每月可获得最大利润,最大利润是多少?24. 如图,二次函数 的图象与 轴交于 , 与 轴交于点 .若点 , 同时从 点出发,都以每秒1个单位长度的速度分别沿 , 边运动,其中一点到达端点时,另一点也随之停止运动. (1)、求该二次函数的解析式及点 的坐标;(2)、当点 运动到 点时,点 停止运动,这时,在 轴上是否存在点 ,使得以 , , 为顶点的三角形为等腰三角形?若存在,请直接写出 点坐标;若不存在,请说明理由.(3)、当 , 运动到 秒时, 沿 翻折,点 恰好落在抛物线上 点处,请判定此时四边形 的形状,并求出 点坐标.25. 如图1,在平面直角坐标系中,点 是坐标原点,四边形 是菱形,点 的坐标为 ,点 在 轴的正半轴上,直线 交 轴于点 , 边交 轴于点 .
(1)、求该二次函数的解析式及点 的坐标;(2)、当点 运动到 点时,点 停止运动,这时,在 轴上是否存在点 ,使得以 , , 为顶点的三角形为等腰三角形?若存在,请直接写出 点坐标;若不存在,请说明理由.(3)、当 , 运动到 秒时, 沿 翻折,点 恰好落在抛物线上 点处,请判定此时四边形 的形状,并求出 点坐标.25. 如图1,在平面直角坐标系中,点 是坐标原点,四边形 是菱形,点 的坐标为 ,点 在 轴的正半轴上,直线 交 轴于点 , 边交 轴于点 .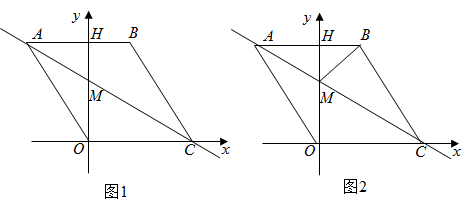 (1)、求直线 的解析式;(2)、连接 ,如图2,动点 从点 出发,沿折线 方向以2个单位/秒的速度向终点 匀速运动,设 的面积为 ( ),点 的运动时间为 秒,求 与 之间的函数关系式(要求写出自变量 的取值范围).(3)、在(2)的条件下,当 为何值时, 与 互为余角,并求此时直线 的解析式.
(1)、求直线 的解析式;(2)、连接 ,如图2,动点 从点 出发,沿折线 方向以2个单位/秒的速度向终点 匀速运动,设 的面积为 ( ),点 的运动时间为 秒,求 与 之间的函数关系式(要求写出自变量 的取值范围).(3)、在(2)的条件下,当 为何值时, 与 互为余角,并求此时直线 的解析式.