陕西省西安市三校2021年数学中考模拟联考试卷
试卷更新日期:2021-06-25 类型:中考模拟
一、单选题
-
1. 在 ,﹣π,0,3.14, ,0. ,﹣7,﹣3 中,无理数有( ).A、1个 B、2个 C、3个 D、4个2. 在下面四个图形中, 与 是对顶角的是( ).A、
 B、
B、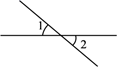 C、
C、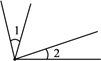 D、
D、 3. 据统计,某城市去年接待旅游人数约为89000000人,89000000这个数据用科学记数法表示为( )A、 B、 C、 D、4. 已知某海水淡化厂淡水储备量为20吨时,刚开始以每小时10吨的淡化的速度加工生产淡水,2小时后,在继续原速度的生产的前提下,为供给市场以每小时15吨的速度运出淡水,则储备淡水量 (吨)与时间 (时)之间的大致图象为( )A、
3. 据统计,某城市去年接待旅游人数约为89000000人,89000000这个数据用科学记数法表示为( )A、 B、 C、 D、4. 已知某海水淡化厂淡水储备量为20吨时,刚开始以每小时10吨的淡化的速度加工生产淡水,2小时后,在继续原速度的生产的前提下,为供给市场以每小时15吨的速度运出淡水,则储备淡水量 (吨)与时间 (时)之间的大致图象为( )A、 B、
B、 C、
C、 D、
D、 5. 下列运算正确的是( )A、a+a=a2 B、(ab)2=ab2 C、a2•a3=a5 D、(a2)3=a56. 如图,Rt△ABC中,∠ACB=90°,以Rt△ABC的三边为边向外作正方形,其面积分别为S1 , S2 , S3 , 且,且S1=4,S3=16,则S2=( )
5. 下列运算正确的是( )A、a+a=a2 B、(ab)2=ab2 C、a2•a3=a5 D、(a2)3=a56. 如图,Rt△ABC中,∠ACB=90°,以Rt△ABC的三边为边向外作正方形,其面积分别为S1 , S2 , S3 , 且,且S1=4,S3=16,则S2=( ) A、20 B、12 C、2 D、27. 下列各点在直线y=2x+6上的是( )A、(﹣5,4) B、(﹣7,20) C、( , ) D、( ,1)8. 在▱ABCD中,AB<BC,对角线AC的垂直平分线交AD于点E,连结CE,若▱ABCD的周长为20cm,则△CDE的周长为( )
A、20 B、12 C、2 D、27. 下列各点在直线y=2x+6上的是( )A、(﹣5,4) B、(﹣7,20) C、( , ) D、( ,1)8. 在▱ABCD中,AB<BC,对角线AC的垂直平分线交AD于点E,连结CE,若▱ABCD的周长为20cm,则△CDE的周长为( ) A、20cm B、40cm C、15cm D、10cm9. 定义:圆心在原点,半径为1的圆称为单位圆.如图,已知点 在单位圆上,则 等于( )
A、20cm B、40cm C、15cm D、10cm9. 定义:圆心在原点,半径为1的圆称为单位圆.如图,已知点 在单位圆上,则 等于( ) A、 B、 C、 D、10. 将抛物线 向下平移3个单位,得到的新抛物线的顶点坐标是( )A、(1,2) B、(2,1) C、(1,5) D、(1, )
A、 B、 C、 D、10. 将抛物线 向下平移3个单位,得到的新抛物线的顶点坐标是( )A、(1,2) B、(2,1) C、(1,5) D、(1, )二、填空题
-
11. 若ab=1,a﹣b=4,则 =.12. 如图,在三角形ABC中,∠ABC=90°,BC=11,把三角形ABC向下平移至三角形DEF后,AD=CG=6,则图中阴影部分的面积为.
 13. 如图,在平面直角坐标系的第一象限中,有一个 ,满足 , , , 轴,当点 ,点 及 的内心 在同一反比例函数 的图象上时,则 的值是.
13. 如图,在平面直角坐标系的第一象限中,有一个 ,满足 , , , 轴,当点 ,点 及 的内心 在同一反比例函数 的图象上时,则 的值是. 14. 如图,AD,BE在AB的同侧,AD=4,BE=4,AB=8,点C为AB的中点,若∠DCE=120°,则DE的最大值是.
14. 如图,AD,BE在AB的同侧,AD=4,BE=4,AB=8,点C为AB的中点,若∠DCE=120°,则DE的最大值是. 15. 小红家的阳台上放置了一个晒衣架,如图1,图2是晒衣架的侧面示意图,立杆AB、CD相交于点O,B、D两点在地面上,经测量得到AB=CD=136cm,OA=OC=51cm,OE=OF=34cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32cm,垂挂在衣架上的连衣裙总长度小于多少时,连衣裙才不会拖在地面上?
15. 小红家的阳台上放置了一个晒衣架,如图1,图2是晒衣架的侧面示意图,立杆AB、CD相交于点O,B、D两点在地面上,经测量得到AB=CD=136cm,OA=OC=51cm,OE=OF=34cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32cm,垂挂在衣架上的连衣裙总长度小于多少时,连衣裙才不会拖在地面上?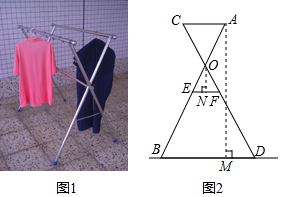
三、解答题
-
16. 解一元一次不等式组:17. 化简: .18. 如图,等腰 ,AC=BC>AB,射线AD与BC交于点D.
 (1)、在射线AD上求作一点E,使得∠CAE=∠AEB;(要求:尺规作图,保留作图痕迹,不写作法)(2)、在(1)的条件下,若CD=2BD,AC=12,求BE的值.19. 如图,P为Rt△ABC斜边AB的中点,过P作PQ∥AC,且PQ=AC.证明:△APQ是等腰三角形.
(1)、在射线AD上求作一点E,使得∠CAE=∠AEB;(要求:尺规作图,保留作图痕迹,不写作法)(2)、在(1)的条件下,若CD=2BD,AC=12,求BE的值.19. 如图,P为Rt△ABC斜边AB的中点,过P作PQ∥AC,且PQ=AC.证明:△APQ是等腰三角形. 20. 为庆祝“五四”青年节,某中学举行了一场书法比赛.比赛结束后,书法老师随机抽取了部分参赛学生的成绩x(x取整数,满分100分)作为样本,整理并绘制成如图不完整的统计图表.
20. 为庆祝“五四”青年节,某中学举行了一场书法比赛.比赛结束后,书法老师随机抽取了部分参赛学生的成绩x(x取整数,满分100分)作为样本,整理并绘制成如图不完整的统计图表.分数段
频数
频率
60≤x<70
30
0.15
70≤x<80
m
0.45
80≤x<90
60
n
90≤x≤100
20
0.1

请根据以上图表提供的信息,解答下列问题:
(1)、表格中m= ▲ ,n= ▲ ,并补全频数分布直方图;(2)、这次抽取的比赛成绩的中位数落在分数段;(3)、全校共有600名学生参加比赛,请你估计成绩不低于80分的学生人数.21. 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段 表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线 表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,请根据图象解答下列问题. (1)、轿车到达乙地时,求货车与甲地的距离.(2)、求线段 对应的函数表达式.(3)、在轿车行进过程中,轿车行驶多少时间,两车相距15千米.22. 甲、乙、丙、丁四位同学参加校田径运动会4×100米接力跑比赛,因为丁的速度最快,所以由他负责跑最后一棒,其他三位同学的跑步顺序随机安排.(1)、请用画树状图或列表的方法表示甲、乙、丙三位同学所有的跑步顺序;(2)、请求出正好由丙将接力棒交给丁的概率.23. 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,点E是边BC的中点.
(1)、轿车到达乙地时,求货车与甲地的距离.(2)、求线段 对应的函数表达式.(3)、在轿车行进过程中,轿车行驶多少时间,两车相距15千米.22. 甲、乙、丙、丁四位同学参加校田径运动会4×100米接力跑比赛,因为丁的速度最快,所以由他负责跑最后一棒,其他三位同学的跑步顺序随机安排.(1)、请用画树状图或列表的方法表示甲、乙、丙三位同学所有的跑步顺序;(2)、请求出正好由丙将接力棒交给丁的概率.23. 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,点E是边BC的中点. (1)、求证:BC2=BD•BA;(2)、判断DE与⊙O位置关系,并说明理由.24. 已知:函数 的图象与 轴相交于点 A(x1 , 0)、B(x2 , 0) 两点 ,与 轴相交于点 , .(1)、求抛物线的解析式且写出其顶点坐标;(2)、连结 ,求 的值.25. 如图1,正方形ABCD和正方形AEFG,连接DG,BE
(1)、求证:BC2=BD•BA;(2)、判断DE与⊙O位置关系,并说明理由.24. 已知:函数 的图象与 轴相交于点 A(x1 , 0)、B(x2 , 0) 两点 ,与 轴相交于点 , .(1)、求抛物线的解析式且写出其顶点坐标;(2)、连结 ,求 的值.25. 如图1,正方形ABCD和正方形AEFG,连接DG,BE (1)、[发现]:当正方形AEFG绕点A旋转,如图2,线段DG与BE之间的数量关系是;位置关系是;(2)、[探究]:如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,猜想DG与BE的数量关系与位置关系,并说明理由;(3)、[应用]:在(2)情况下,连结GE(点E在AB上方),若GE//AB,且AB= ,AE=1,求线段DG的长
(1)、[发现]:当正方形AEFG绕点A旋转,如图2,线段DG与BE之间的数量关系是;位置关系是;(2)、[探究]:如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,猜想DG与BE的数量关系与位置关系,并说明理由;(3)、[应用]:在(2)情况下,连结GE(点E在AB上方),若GE//AB,且AB= ,AE=1,求线段DG的长