江苏省盐城市盐城市2021年数学中考二模试卷
试卷更新日期:2021-06-25 类型:中考模拟
一、单选题
-
1. 实数-5的相反数是( )A、-5 B、 C、 D、52. 冬季奥林匹克运动会是世界规模最大的冬季综合性运动会,每四年举办一次,第24届冬奥会将于2022年在北京和张家口举办.下列四个图分别是第24届冬奥会图标中的一部分,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 正八边形的内角和为( )A、360° B、540° C、1080° D、720°4. 在下列四个数中,属于无理数的是( )A、 B、 C、-1 D、5. 如图,点A,B,C在⊙O上,∠AOB=72°,则∠ACB等于( )
3. 正八边形的内角和为( )A、360° B、540° C、1080° D、720°4. 在下列四个数中,属于无理数的是( )A、 B、 C、-1 D、5. 如图,点A,B,C在⊙O上,∠AOB=72°,则∠ACB等于( ) A、36° B、54° C、18° D、28°6. 下面不是正方体展开图的是( )A、
A、36° B、54° C、18° D、28°6. 下面不是正方体展开图的是( )A、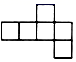 B、
B、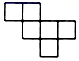 C、
C、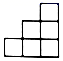 D、
D、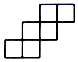 7. 下表是一组二次函数 的自变量x与函数值y的对应值:
7. 下表是一组二次函数 的自变量x与函数值y的对应值:
1
1.1
1.2
1.3
1.4
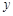
-1
-0.49
0.04
0.59
1.16
那么方程 的一个近似根是( )
A、1 B、1.1 C、1.2 D、1.38. 如图,点A、B分别是反比例函数y= 、y= 图象上的点,当∠AOB=90°时tanA=3,则 的值为( ) A、 B、 C、9 D、-9
A、 B、 C、9 D、-9二、填空题
-
9. 因式分解: .
10. 盐城市2021年5月1日的最高气温19℃,最低气温9℃,则当天气温的极差为℃.11. 全世界出现新冠肺炎疫情,研究发现新冠肺炎病毒大小约为125nm,已知1nm=0.000000001米,用科学记数法表示一个新冠病毒的大小为米.12. 如图,一个转盘被分为了A,B,C三个区域,自由转动转盘一次,当转盘停止时,指针指向A区域的概率是. 13. 圆锥的母线长是5 cm,底面半径长是3 cm,它的侧面展开图的圆心角是.14. 如图,在⊙O中,弦CD过弦AB的中点E,CE=1,DE=3,则AB=.
13. 圆锥的母线长是5 cm,底面半径长是3 cm,它的侧面展开图的圆心角是.14. 如图,在⊙O中,弦CD过弦AB的中点E,CE=1,DE=3,则AB=.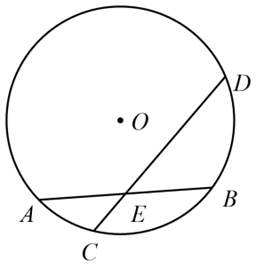 15. 已知 中, , , ,则 的长等于16. 如图,在△ABC中,AB=AC=5,BC=6,点P是AB边上一点,且AP=2,动点M从点P出发,沿P→B→C运动,作∠AMQ=∠B与AC相交于点Q,则在点M运动的过程中,点Q的运动路径长为.
15. 已知 中, , , ,则 的长等于16. 如图,在△ABC中,AB=AC=5,BC=6,点P是AB边上一点,且AP=2,动点M从点P出发,沿P→B→C运动,作∠AMQ=∠B与AC相交于点Q,则在点M运动的过程中,点Q的运动路径长为.
三、解答题
-
17. 计算:18. 解方程: .19. 先化简,再求值: ,其中x2﹣6x+7=0.20. 如图,矩形ABCD对角线AC、BD相交于点O,分别过点D、点A作直线DE∥AC,直线AE∥BD,交于点E.
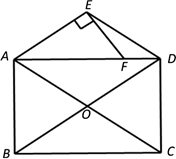 (1)、求证:四边形AODE是菱形;(2)、点E作EF⊥AE交AD于点F,若AB=2,BC=4,求EF.21. 2021年是中国共产党成立100周年和“十四五”规划开局之年,也是开启全面建设社会主义现代化国家新征程的第一年,在这个重要历史节点召开的全国两会,备受瞩目.某校组织开展了以“聚焦两会,关注祖国发展”为主题的阅读活动,受到老师们的广泛关注和同学们的积极响应.为了解全校学生关注两会的情况,该校学生会随机抽查了20名学生在某一周阅读关于两会文章的篇数,并进行了以下数据的整理与分析:
(1)、求证:四边形AODE是菱形;(2)、点E作EF⊥AE交AD于点F,若AB=2,BC=4,求EF.21. 2021年是中国共产党成立100周年和“十四五”规划开局之年,也是开启全面建设社会主义现代化国家新征程的第一年,在这个重要历史节点召开的全国两会,备受瞩目.某校组织开展了以“聚焦两会,关注祖国发展”为主题的阅读活动,受到老师们的广泛关注和同学们的积极响应.为了解全校学生关注两会的情况,该校学生会随机抽查了20名学生在某一周阅读关于两会文章的篇数,并进行了以下数据的整理与分析:①数据收集,抽取的20名学生阅读关于两会文章的篇数如下(单位:篇):5,3,3,4,5,4,6,7,4,6,6,7,6,5,4,5,5,6,4,6.
②数据整理,将收集的数据进行分组并绘制成不完整的扇形统计图:
阅读的篇数(篇)
3
4
5
6
7
人数
2
a
5
6
2
③数据分析(单位:篇):
众数
中位数
平均数
6
m
n
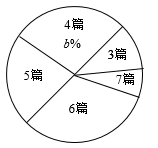
依据统计信息回答问题:
(1)、扇形统计图中,“6篇”对应的扇形圆心角度数为°,b=;(2)、求数据分析中m和n的值;(3)、若该校共有1000名学生,根据抽查结果,估计该校学生在这一周内阅读关于两会文章篇数为4篇的人数.22. 如图是我们熟悉的电路图,其中L1、L2、L3代表灯泡,K1、K2、K3、K4代表开关,R代表电阻.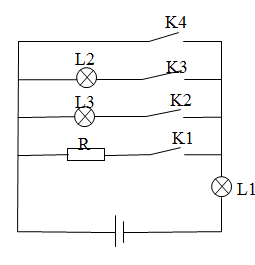 (1)、合上一个开关,有两盏灯亮的概率是;(2)、合上两个开关,有两盏灯亮的概率是多少?请结合树状图或表格解决问题.23. 已知:如图,在△ABC中,∠ACB=90°.
(1)、合上一个开关,有两盏灯亮的概率是;(2)、合上两个开关,有两盏灯亮的概率是多少?请结合树状图或表格解决问题.23. 已知:如图,在△ABC中,∠ACB=90°. (1)、求作⊙O,使点O在BC上,且⊙O与AC、AB都相切;(保留作图痕迹,不写作法)(2)、若AC=8,BC=15,求⊙O半径.24. 如图,一次函数y=x+1与反比例函数 交于A、B两点,其中A点坐标为(1,m).
(1)、求作⊙O,使点O在BC上,且⊙O与AC、AB都相切;(保留作图痕迹,不写作法)(2)、若AC=8,BC=15,求⊙O半径.24. 如图,一次函数y=x+1与反比例函数 交于A、B两点,其中A点坐标为(1,m).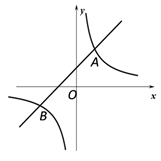 (1)、求m、k;(2)、在x轴上是否存在点C,使S△ABC=3?若存在,求点C的坐标;若不存在,请说明理由.25. 超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加 元,每天售出 件.(1)、请写出 与 之间的函数表达式;(2)、当 为多少时,超市每天销售这种玩具可获利润2250元?(3)、设超市每天销售这种玩具可获利 元,当 为多少时 最大,最大值是多少?26. 在△ABC中,AC=BC=3,∠ACB=90°,D为线段AC上一点,AD=1.过点D作DE∥BC交AB于点E, M为DE的中点.
(1)、求m、k;(2)、在x轴上是否存在点C,使S△ABC=3?若存在,求点C的坐标;若不存在,请说明理由.25. 超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加 元,每天售出 件.(1)、请写出 与 之间的函数表达式;(2)、当 为多少时,超市每天销售这种玩具可获利润2250元?(3)、设超市每天销售这种玩具可获利 元,当 为多少时 最大,最大值是多少?26. 在△ABC中,AC=BC=3,∠ACB=90°,D为线段AC上一点,AD=1.过点D作DE∥BC交AB于点E, M为DE的中点. (1)、如图1,连接BD,取BD的中点N,求线段MN的长;(2)、如图2,将△ADE绕点A逆时针旋转,旋转角为α,F、N分别为线段CB、DB的中点,连接FN,MN.猜想∠FNM的大小是否为定值,并证明你的结论;(3)、在(2)的条件下,连接CN,在△ADE绕点A逆时针旋转过程中,当线段CN最大时,请直接写出△FCN的面积.27. 将抛物线y=ax2的图象(如图1)绕原点顺时针旋转90度后可得新的抛物线图象(如图2),记为C:y2= x.
(1)、如图1,连接BD,取BD的中点N,求线段MN的长;(2)、如图2,将△ADE绕点A逆时针旋转,旋转角为α,F、N分别为线段CB、DB的中点,连接FN,MN.猜想∠FNM的大小是否为定值,并证明你的结论;(3)、在(2)的条件下,连接CN,在△ADE绕点A逆时针旋转过程中,当线段CN最大时,请直接写出△FCN的面积.27. 将抛物线y=ax2的图象(如图1)绕原点顺时针旋转90度后可得新的抛物线图象(如图2),记为C:y2= x.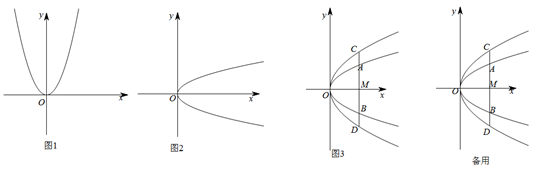
(概念与理解)
(1)、将抛物线y1=4x2和y2=x2按上述方法操作后可得新的抛物线图象,记为:C1:;C2:.(2)、(猜想与证明) 在平面直角坐标系中,点M(x,0)在x轴正半轴上,过点M作平行于y轴的直线,分别交抛物线C1于点A、B,交抛物线C2于点C、D,如图3所示.
填空:当x=1时, =;当x=2时, =;(3)、猜想:对任意x(x>0)上述结论是否仍然成立?若成立,请证明你的猜想;若不成立,请说明理由.(4)、(探究与应用)
①利用上面的结论,可得△AOB与△COD面积比为 ;②若△AOB和△COD中有一个是直角三角形时,求△COD与△AOB面积之差;
(5)、(联想与拓展)
若抛物线C3:y2=mx、C4:y2=nx(0<m<n),M(k,0)在x轴正半轴上,如图所示,过点M作平行于y轴的直线,分别交抛物线C3于点A、B,交抛物线C4于点C、D.过点A作x轴的平行线交抛物线C4于点E,过点D作x轴的平行线交抛物线C3于点F.对于x轴上任取一点P,均有△PAE与△PDF面积的比值1:3,请直接写出m和n之间满足的等量关系是.