江苏省徐州市邳州市2021年数学中考二模试卷
试卷更新日期:2021-06-25 类型:中考模拟
一、单选题
-
1. 与-3互为相反数的是( )A、-3 B、3 C、- D、2. 国家统计局12月18日发布公告,经初步统计,2020年全国棉花播种面积约为3170000公顷.将3170000用科学记数法表示为( )A、 B、 C、 D、3. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、等边三角形 B、平行四边形 C、矩形 D、正五边形4. 下列计算正确的是( )A、 B、 C、 D、5. 将二次函数 的图象向上平移2个单位后得到的新抛物线的表达式为( )A、 B、 C、 D、6. 如图,是小明绘制的他在一周内每天跑步圈数的折线统计图.下列结论正确的是( )
 A、中位数是9 B、众数是9 C、平均数是10 D、方差是37. 如图, 是⊙O的直径, 、 是⊙O上的两点, ,则 的度数为( )
A、中位数是9 B、众数是9 C、平均数是10 D、方差是37. 如图, 是⊙O的直径, 、 是⊙O上的两点, ,则 的度数为( ) A、60° B、65° C、70° D、75°8. 如图,在平面直角坐标系中,以坐标原点 , , 为顶点的 ,其两个锐角对应的外角角平分线相交于点 ,且点 恰好在反比例函数 的图象上,则 的值为( )
A、60° B、65° C、70° D、75°8. 如图,在平面直角坐标系中,以坐标原点 , , 为顶点的 ,其两个锐角对应的外角角平分线相交于点 ,且点 恰好在反比例函数 的图象上,则 的值为( )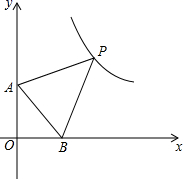 A、25 B、36 C、49 D、64
A、25 B、36 C、49 D、64二、填空题
-
9. 的立方根是 .10. 若 在实数范围内有意义,则x的取值范围是.11. 若 ,则 .12. 若正比例函数y=kx的图象经过点(1,2),则k= .13. 方程 的解为.14. 如图所示,若用半径为6,圆心角为120°的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的底面半径是.
 15. 设函数 与 的图象的交点坐标为 ,则 值是.16. 如图,菱形 的两条对角线 相交于点 是 的中点,若 ,则 的长为.
15. 设函数 与 的图象的交点坐标为 ,则 值是.16. 如图,菱形 的两条对角线 相交于点 是 的中点,若 ,则 的长为.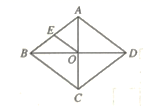 17. 如图,在 中, 是 边上的高, , , ,则 的长为.
17. 如图,在 中, 是 边上的高, , , ,则 的长为.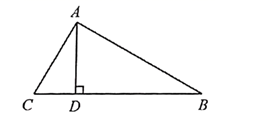 18. 如图,在平面直角坐标系中,直线 为正比例函数 的图象,点 的坐标为(1,0),过点 作 轴的垂线交直线 于点 ,以 为边作正方形 ;过点 作直线 的垂线,垂足为 ,交 轴于点 ,以 为边作正方形 ;过点 作 轴的垂线,垂足为 ,交直线 于点 ,以 为边作正方形 ,…,按此规律操作下所得到的正方形 的面积是.
18. 如图,在平面直角坐标系中,直线 为正比例函数 的图象,点 的坐标为(1,0),过点 作 轴的垂线交直线 于点 ,以 为边作正方形 ;过点 作直线 的垂线,垂足为 ,交 轴于点 ,以 为边作正方形 ;过点 作 轴的垂线,垂足为 ,交直线 于点 ,以 为边作正方形 ,…,按此规律操作下所得到的正方形 的面积是.
三、解答题
-
19. 计算:(1)、 ;(2)、 .20.(1)、解方程: ;(2)、解不等式组:21. 为发展学生的核心素养,培养学生的综合能力,某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行整理,绘制成两幅不完整的统计图,请结合图中所给信息解答下列问题:
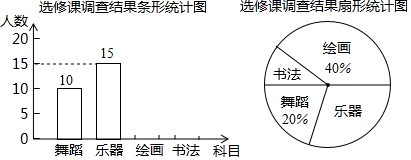 (1)、参与随机抽样问卷调查的有 ▲ 名学生,并补全条形统计图;(2)、扇形统计图中,“乐器”所对应的圆心角度数是°;(3)、若该校有600名学生,估计选修书法的学生大约有多少名?22. “中国结”是我国特有的手工编织工艺品,也是一种传统吉祥装饰物.如图,现有三张正面印有“中国结”图案的不透明卡片 , , ,卡片除正面图案不同外,其余均相同.将三张卡片正面向下洗匀,小吉同学从中随机抽取一张卡片,记下图案后正面向下放回,洗匀后再从中随机抽取一张卡片,请用画树状图或列表的方法,求小吉同学抽出的两张卡片中至少有一张是 卡片的概率.
(1)、参与随机抽样问卷调查的有 ▲ 名学生,并补全条形统计图;(2)、扇形统计图中,“乐器”所对应的圆心角度数是°;(3)、若该校有600名学生,估计选修书法的学生大约有多少名?22. “中国结”是我国特有的手工编织工艺品,也是一种传统吉祥装饰物.如图,现有三张正面印有“中国结”图案的不透明卡片 , , ,卡片除正面图案不同外,其余均相同.将三张卡片正面向下洗匀,小吉同学从中随机抽取一张卡片,记下图案后正面向下放回,洗匀后再从中随机抽取一张卡片,请用画树状图或列表的方法,求小吉同学抽出的两张卡片中至少有一张是 卡片的概率. 23. 如图, 的对角线 、 相交于点 ,过点 作 ,分别交 、 于点 、 ,连接 、 .
23. 如图, 的对角线 、 相交于点 ,过点 作 ,分别交 、 于点 、 ,连接 、 .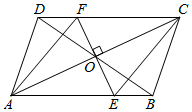 (1)、若 ,求 的长;(2)、判断四边形 的形状,并说明理由.24. 某停车场的收费标准如下:中型汽车的停车费为12元/辆,小型汽车的停车费为7元/辆.现在停车场内停有28辆中、小型汽车,这些车共缴纳停车费246元,求中小型汽车各有多少辆?25. 如图,⊙O为锐角△ABC的外接圆,半径为5.
(1)、若 ,求 的长;(2)、判断四边形 的形状,并说明理由.24. 某停车场的收费标准如下:中型汽车的停车费为12元/辆,小型汽车的停车费为7元/辆.现在停车场内停有28辆中、小型汽车,这些车共缴纳停车费246元,求中小型汽车各有多少辆?25. 如图,⊙O为锐角△ABC的外接圆,半径为5.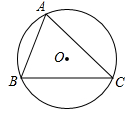 (1)、用尺规作图作出∠BAC的平分线,并标出它与劣弧BC的交点E(保留作图痕迹,不写作法);
(1)、用尺规作图作出∠BAC的平分线,并标出它与劣弧BC的交点E(保留作图痕迹,不写作法);
(2)、若(1)中的点E到弦BC的距离为3,求弦CE的长.26. 某水果超市以每千克20元的价格购进一批樱桃,规定每千克樱桃售价不低于进价又不高于40元,经市场调查发现,樱桃的日销售量 (千克)与每千克售价 (元)满足一次函数关系,其部分对应数据如下表所示:每千克售价 (元)
…
25
30
35
…
日销售量 (千克)
…
102
92
82
…
(1)、求 与 之间的函数表达式;(2)、该超巿要想获得1280元的日销售利润,每千克樱桃的售价应定为多少元?(3)、当每千克樱桃的售价定为元时,日销售利润最大,最大利润是元.27. 在矩形 中, , ,点 是边 上一动点,连接 ,将 沿 翻折,点 的对应点为点 .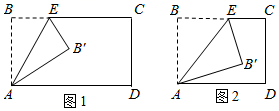 (1)、如图,设 , ,在点 从 点运动到 点的过程中.
(1)、如图,设 , ,在点 从 点运动到 点的过程中.① 最小值是 , 此时x=;
②点 的运动路径长为.
(2)、如图,设 ,当点 的对应点 落在矩形 的边上时,求 的值.28. 如图,二次函数 的图象与 轴交于 、 两点,与 轴交于点 . (1)、求二次函数的表达式;(2)、若点 为抛物线对称轴上一动点,当 是直角三角形时,请直接写出点 的坐标;(3)、若点 为抛物线上的一个动点,将点 绕原点 旋转180°得到点 .
(1)、求二次函数的表达式;(2)、若点 为抛物线对称轴上一动点,当 是直角三角形时,请直接写出点 的坐标;(3)、若点 为抛物线上的一个动点,将点 绕原点 旋转180°得到点 .①当点 落在该抛物线上时,求 的值;
②当点 落在第二象限内且 取得最小值时,求 的值.