江苏省无锡市侨谊集团2021年数学中考二模试卷
试卷更新日期：2021-06-25 类型：中考模拟
一、单选题
-
1. 2的倒数是（ ）A、 2 B、﹣2 C、 D、2. 下列图形中，是中心对称图形但不是轴对称图形的是（ ）A、
B、
C、
D、
3. 下列运算正确的是（ ）A、（a2）3=a5 B、a4·a2=a8 C、a6÷a3=a² D、（ab）3=a3b34. 一个几何体的三视图如图所示，则这个几何体是（ ）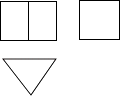
A、圆柱 B、圆锥 C、三棱柱 D、长方体5. 某鞋厂调查了商场一个月内不同尺码男鞋的销量，在以下统计量中，该鞋厂最关注的是（ ）A、平均数 B、中位数 C、众数 D、方差6. 如图，在半径为 的圆形纸片中，剪一个圆心角为90°的最大扇形（阴影部分），则这个扇形的面积为 （ ）
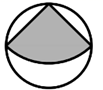A、π B、 C、2π D、7. 如图，A为反比例函数y＝ （其中x＞0）图象上的一点，在x轴正半轴上有一点B，OB＝6.连接OA，AB，且OA＝AB.过点B作BC⊥OB，交反比例函数y＝ （其中x＞0）的图象于点C，连接OC交AB于点D，S△OBC＝6，则AB的长度为（ ）
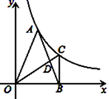A、4 B、5 C、5 D、58. 如图，已知线段AB，分别以A，B为圆心，大于 AB同样长为半径画弧，两弧交于点C，D，连接AC，AD，BC，BD，CD，则下列说法错误的是（ ）
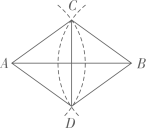A、AB平分∠CAD B、CD平分∠ACB C、AB⊥CD D、AB=CD9. 点P（a，b）在以y轴为对称轴的二次函数y＝ ＋mx＋5的图象上，则2a－b的最大值等于（ ）A、4 B、－4 C、－4.5 D、4.510. 如图，C为线段AB上一点，在线段AB的同侧分别作等边△ACD、△BCE，连接AE、BD相交于F，连接CF.若S△DEF＝8 ，则CF的长为（ ）
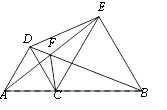A、4 B、3 C、3 D、4二、填空题
-
11. 如果分式 有意义，那么实数x的取值范围是 ．12. 地球与太阳的平均距离大约为150 000 000km，用科学记数法表示km．13. 正十边形的每一个内角的度数为.14. 若一组数据3，4，5，x，6，7的平均数是5，则x的值是.15. 如图，菱形ABOC的AB，AC分别与⊙O相切于点D、E，若点D是AB的中点，则∠DOE=.
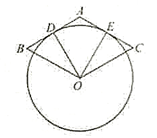16. 把一张宽为2cm的长方形纸片ABCD折叠成如图所示的阴影图案，顶点A，D互相重合，中间空白部分是以E为直角顶点，腰长为4cm的等腰直角三角形，则纸片的长AD为 cm.
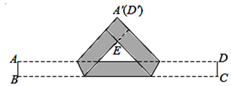17. 如图，在平面直角坐标系中，A（3，0），B（0，4），M为AB边上的一动点，N（0，1），连接MN，将△ABO绕点O逆时针旋转一周，则MN的取值范围为.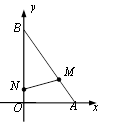
三、解答题
-
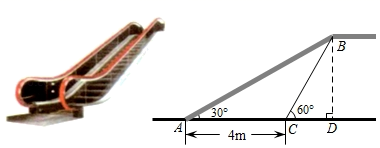
18. 如图是某商场营业大厅自动扶梯示意图.自动扶梯AB的倾斜角为30°，在自动扶梯下方地面C处测得扶梯顶端B的仰角为60°，A、C之间的距离为4m. 则自动扶梯的垂直高度BD＝.
19. 计算：(1)、2sin45°－(－1)0＋( )－2；(2)、3(x2＋2)－3(x＋1)(x－1).20.(1)、解方程：(2)、解方程： .21. 如图，等边△AEF的顶点E，F在矩形ABCD的边BC，CD上，且∠CEF＝45°.求证：矩形ABCD是正方形.
22. 已知不等式组(1)、求不等式组的解集，并写出它的所有整数解；(2)、在不等式组的所有整数解中任取两个不同的整数相乘，请用画树状图或列表的方法求积为非负数的概率.23. 为了解某校学生的课余兴趣爱好情况，某调查小组设计了“阅读”、“打球”、“书法”和“舞蹈”四个选项，用随机抽样的方法调查了该校部分学生的课余兴趣爱好情况（每个学生必须选一项且只能选一项），并根据调查结果绘制了如图统计图：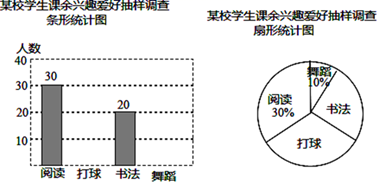
根据统计图所提供的信息，解答下列问题：
(1)、本次抽样调查中的学生人数是；(2)、补全条形统计图；(3)、若该校共有1000名学生，请根据统计结果估计该校课余兴趣爱好为“打球”的学生人数.24. 按要求完成下列尺规作图（不写作法，保留作图痕迹）.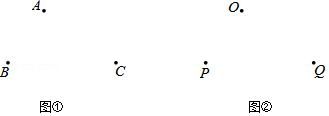
(1)、如图①，点A、B、C是平行四边形ABCD的三个顶点，求作平行四边形ABCD；(2)、如图②，点O、P、Q分别是平行四边形EFGH三边EH、EF、FG的中点，求作平行四边形EFGH.25. 如图，已知AB是⊙O的直径，C是⊙O上的一点，D是AB上的一点，DE⊥AB于D ， DE交BC于F ， 且EF＝EC ．
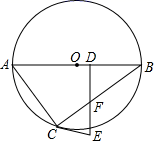(1)、求证：EC是⊙O的切线；(2)、若BD＝4，BC＝8，圆的半径OB＝5，求切线EC的长．26. 某地新建的一个企业，每月将产生2020吨污水，为保护环境，该企业计划购置污水处理器，并在如下两个型号中选择：污水处理器型号
A型
B型
处理污水能力（吨/月）
240
180
已知商家售出的2台A型、3台B型污水处理器的总价为44万元；售出的1台A型、4台B型污水处理器的总价为42万元.
(1)、求每台A型、B型污水处理器的价格；(2)、为确保将每月产生的污水全部处理完，该企业决定购买上述A、B两种型号污水处理器共9台，那么①该企业有几种购买方案？
②哪种方案费用最低？最低费用是多少？
27. 定义：长宽比为 ：1（n为正整数）的矩形称为 矩形.下面，我们通过折叠的方式折出一个 矩形，如图a所示.
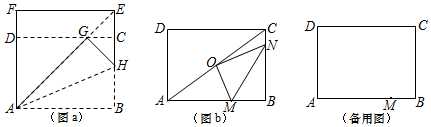
操作1：将正方形ABEF沿过点A的直线折叠，使折叠后的点B落在对角线AE上的点G处，折痕为AH.
操作2：将FE沿过点G的直线折叠，使点F、点E分别落在边AF，BE上，折痕为CD.则四边形ABCD为 矩形.
(1)、证明：四边形ABCD为 矩形；(2)、点M是边AB上一动点.①如图b，O是对角线AC的中点，若点N在边BC上，OM⊥ON，连接MN.求tan∠OMN的值；
②若AM=AD，点N在边BC上，当△DMN的周长最小时，求 的值；
③连接CM，作BR⊥CM，垂足为R.若AB=2 ，则DR的最小值= ▲ .
28. 如图，抛物线y＝x2＋bx＋c与x轴分别交于A，B两点（点A在点B的左侧），与y轴交于点C，且OB＝OC＝3OA.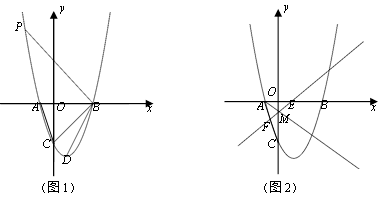
(1)、求该抛物线的函数表达式；(2)、如图1，点D是该抛物线的顶点，点P(m，n)是第二象限内抛物线上的一个点，分别连接BD、BC、BP，当∠PBA＝2∠CBD时，求m的值；(3)、如图2，∠BAC的角平分线交y轴于点M，过M点的直线l与射线AB，AC分别于E，F，已知当直线l绕点M旋转时， ＋ 为定值，请直接写出该定值.