江苏省常州市溧阳市2021年数学中考一模试卷
试卷更新日期:2021-06-25 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、-2 B、2 C、 D、2. 下列计算结果正确的是( )A、 B、 C、 D、3. 下列几何体中,圆柱是( )A、
 B、
B、 C、
C、 D、
D、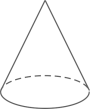 4. 把一副三角板放在同一水平桌面上,摆放成如图所示的形状,使两个直角顶点重合,两条斜边平行,则∠1的度数是( )
4. 把一副三角板放在同一水平桌面上,摆放成如图所示的形状,使两个直角顶点重合,两条斜边平行,则∠1的度数是( )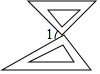 A、45° B、60° C、75° D、82.5°5. 如图, 中,弦 , 相交于点P, , ,则 的度数是( )
A、45° B、60° C、75° D、82.5°5. 如图, 中,弦 , 相交于点P, , ,则 的度数是( ) A、 B、 C、 D、6. 广阔无垠的太空中有无数颗恒星,其中离太阳系最近的一颗恒星称为“比邻星”,它距离太阳系约4.2光年.光年是天文学中一种计量天体时空距离的长度单位,1光年约为9500000000000千米.则“比邻星”距离太阳系约为( )A、 千米 B、 千米 C、 千米 D、 千米7. 如图,在 中, ,沿图中虚线 翻折,使得点B落在 上的点D处,则 等于( )
A、 B、 C、 D、6. 广阔无垠的太空中有无数颗恒星,其中离太阳系最近的一颗恒星称为“比邻星”,它距离太阳系约4.2光年.光年是天文学中一种计量天体时空距离的长度单位,1光年约为9500000000000千米.则“比邻星”距离太阳系约为( )A、 千米 B、 千米 C、 千米 D、 千米7. 如图,在 中, ,沿图中虚线 翻折,使得点B落在 上的点D处,则 等于( ) A、160° B、150° C、140° D、110°8. 已知 是半径为1的 的一条弦,且 ,以 为一边在 内作等边三角形 ,D为 上不同于点A的一点,且 , 的延长线交 于点E,则 的长为( )
A、160° B、150° C、140° D、110°8. 已知 是半径为1的 的一条弦,且 ,以 为一边在 内作等边三角形 ,D为 上不同于点A的一点,且 , 的延长线交 于点E,则 的长为( ) A、 B、1 C、 D、a
A、 B、1 C、 D、a二、填空题
-
9. 计算: .10. 计算: + = .11. 分解因式: .12. 若 在实数范围内有意义,则实数x的取值范围是 .13. 已知关于x的方程 的一个根是2,则 .14. 用半径为2cm的半圆围成一个圆锥的侧面,则这个圆锥的底面半径为.15. 在某公司的面试中,李明的得分情况为:个人形象85分,工作能力90分,交际能力80分,已知个人形象、工作能力和交际能力的权重为1: 2: 2,则李明的最终成绩是 .16. 如图,每一个小方格的边长都相等,点A、B、C三点都在格点上,则 的值为.
 17. 如图,在 中, ,点D是 上一点, ,若 ,则 .
17. 如图,在 中, ,点D是 上一点, ,若 ,则 . 18. 如图,四边形 的四个顶点分别在反比例函数 与 的图象上,对角线 轴,且 .已知点A的横坐标为4,当四边形 是正方形时,请写出m、n之间的数量关系.
18. 如图,四边形 的四个顶点分别在反比例函数 与 的图象上,对角线 轴,且 .已知点A的横坐标为4,当四边形 是正方形时,请写出m、n之间的数量关系.
三、解答题
-
19. 计算:20. 解方程和不等式组(1)、(2)、21. 在正方形ABCD中,AC为对角线,E为AC上一点,连接EB、ED.
 (1)、求证:△BEC≌△DEC;(2)、延长BE交AD于F,当∠BED=120°时,求∠EFD的度数.22. “只要人人献出一点爱,世界将变成美好的人间”.某单位利用“世界献血日”开展自愿义务献血活动,经过检测,献血者血型有“A、B、 、O”四种类型,随机抽取部分献血结果进行统计,根据结果制作了如图两幅不完整统计图表(表、图)
(1)、求证:△BEC≌△DEC;(2)、延长BE交AD于F,当∠BED=120°时,求∠EFD的度数.22. “只要人人献出一点爱,世界将变成美好的人间”.某单位利用“世界献血日”开展自愿义务献血活动,经过检测,献血者血型有“A、B、 、O”四种类型,随机抽取部分献血结果进行统计,根据结果制作了如图两幅不完整统计图表(表、图)血型统计表:血型统计图:
血型
A
B
O
人数
______
10
5
______
 (1)、本次随机抽取献血者人数为人,图中 ;(2)、补全表中的数据;(3)、若这次活动中该单位有1300人义务献血,估计大约有多少人是A型血?23. 四张扑克牌的点数分别是2、3、4、8,将它们洗匀后背面朝上放在桌面上.(1)、从中随机抽取一张牌,求这张牌的点数是偶数的概率;(2)、从中先随机抽取一张牌,接着再抽取一张牌,求这两张牌的点数都是偶数的概率.24. 开学初,小芳和小亮去学校商店购买学习用品,小芳用18元钱买了1支钢笔和3本笔记本,小亮用31元买了同样的钢笔2支和笔记本5本.
(1)、本次随机抽取献血者人数为人,图中 ;(2)、补全表中的数据;(3)、若这次活动中该单位有1300人义务献血,估计大约有多少人是A型血?23. 四张扑克牌的点数分别是2、3、4、8,将它们洗匀后背面朝上放在桌面上.(1)、从中随机抽取一张牌,求这张牌的点数是偶数的概率;(2)、从中先随机抽取一张牌,接着再抽取一张牌,求这两张牌的点数都是偶数的概率.24. 开学初,小芳和小亮去学校商店购买学习用品,小芳用18元钱买了1支钢笔和3本笔记本,小亮用31元买了同样的钢笔2支和笔记本5本.
(1)、求每支钢笔和每本笔记本的价格;(2)、校运会后,班主任拿出200元学校奖励基金交给班长,购买上述价格的钢笔和笔记本共48件作为奖品,奖给校运会表现突出的同学,要求笔记本数不少于钢笔数.请问:有多少购买方案?请你一一写出.
25. 如图,将 放在平面直角坐标系中, , ,反比例函数 经过点A.在反比例函数的图象上取一点C,使得 ,过点C作 的垂线,交 于点D,连接 ,并延长 交 于点E. (1)、求反比例函数的表达式;(2)、当点E刚好是 的中点时,求 的度数.26. 如图,在直角坐标系中,点 .
(1)、求反比例函数的表达式;(2)、当点E刚好是 的中点时,求 的度数.26. 如图,在直角坐标系中,点 . (1)、求出点B的坐标;(2)、将 绕点C顺时针旋转一定角度得到 ,旋转后当点 落在y轴上时,直接写出此时点 的坐标;(3)、当直线 经过点B时,求直线 的函数表达式.27. 在同一平面内,具有一条公共边且不完全重合的两个全等三角形,我们称这两个三角形叫做“共边全等”(1)、下列图形中两个三角形不是“共边全等”是;
(1)、求出点B的坐标;(2)、将 绕点C顺时针旋转一定角度得到 ,旋转后当点 落在y轴上时,直接写出此时点 的坐标;(3)、当直线 经过点B时,求直线 的函数表达式.27. 在同一平面内,具有一条公共边且不完全重合的两个全等三角形,我们称这两个三角形叫做“共边全等”(1)、下列图形中两个三角形不是“共边全等”是; (2)、如图1,在边长为6的等边三角形 中,点D在 边上,且 ,点E、F分别在 、 边上,满足 和 为“共边全等”,求 的长;
(2)、如图1,在边长为6的等边三角形 中,点D在 边上,且 ,点E、F分别在 、 边上,满足 和 为“共边全等”,求 的长; (3)、如图2,在平面直角坐标系中,直线 分别与直线 、x轴相交于A、B两点,点C是 的中点,P、Q在 的边上,当以P、B、Q为顶点的三角形与 “共边全等”时,请直接写出点Q的坐标.
(3)、如图2,在平面直角坐标系中,直线 分别与直线 、x轴相交于A、B两点,点C是 的中点,P、Q在 的边上,当以P、B、Q为顶点的三角形与 “共边全等”时,请直接写出点Q的坐标. 28. 如图所示,抛物线 的图象与x轴交于A、B两点,与y轴交于点C.
28. 如图所示,抛物线 的图象与x轴交于A、B两点,与y轴交于点C. (1)、当 时 ,
(1)、当 时 ,①求点A、B、C的坐标;
②如果点P是抛物线上一点,点M是该抛物线对称轴上的点,当 是以 为斜边的等腰直角三角形时,求出点P的坐标;
(2)、点D是抛物线的顶点,连接 、 ,当四边形 是圆的内接四边形时,求a的值.