湖南省株洲市茶陵县2021年数学中考模拟试卷

试卷更新日期：2021-06-25 类型：中考模拟

进入出卷网下载

一、单选题

1. $- \frac{2}{3}$ 的绝对值是（）

A、 $\frac{3}{2}$ B、 $\frac{2}{3}$ C、-1 D、 $- \frac{3}{2}$

查看试题解析
2. 单项式9x^my³与单项式4x²yⁿ是同类项，则m＋n的值是（）

A、2 B、5 C、4 D、3

查看试题解析
3. 下列运算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 ${(a^{2})}^{3} = a^{5}$ C、 $a^{5} + a^{5} = 2 a^{5}$ D、 $a^{8} \div a^{4} = a^{2}$

查看试题解析
4. 下列手机手势解锁图案中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 下列说法正确的是（）

A、概率很小的事件不可能发生 B、随机事件发生的概率为1 C、不可能事件发生的概率为0 D、投掷一枚质地均匀的硬币1000次，正面朝上的次数一定是500次

查看试题解析
6. 在直角坐标系中，点P（m，2—2m）的横坐标与纵坐标互为相反数，则P点在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 如果m＝ $\sqrt{12}$ ﹣1，那么m的取值范围是（）

A、0＜m＜1 B、1＜m＜2 C、2＜m＜3 D、3＜m＜4

查看试题解析
8. 如图，要拧开一个边长为a＝6 mm的正六边形螺帽，扳手张开的开口b至少为（）

A、6 $\sqrt{2}$ mm B、12mm C、6 $\sqrt{3}$ mm D、4 $\sqrt{3}$ mm

查看试题解析
9. 在我国古代数学著作《九章算术》的第九章《勾股》中记载了这样一个问题：“今天有开门去阔一尺，不合二寸，问门广几何?”意思是：如图，推开两扇门(AD和BC)，门边缘D，C两点到门槛AB的距离是1尺，两扇门的间隙CD为2寸，则门宽AB长是（）寸(1尺=10寸)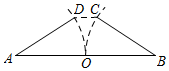

A、101 B、100 C、52 D、96

查看试题解析
10. 如图，反比例函数 $y = \frac{k}{x}$ 的图象经过二次函数y=ax²+bx图象的顶点（– $\frac{1}{2}$ ，m）（m>0），则有（）

A、a=b+2k B、a=b–2k C、k<b<0 D、a<k<0

查看试题解析

二、填空题

11. 数轴上表示3的点到原点的距离是 .

查看试题解析
12. 分解因式： $m^{3} n - 9 m n$ ＝.

查看试题解析
13. 某班五个合作学习小组人数如下：5、5、 $x$ 、6、7，已知这组数据的平均数是6，则这组数据的中位数是

查看试题解析
14. 若a＜1，化简 $\sqrt{{(a - 1)}^{2}} - 1$ ＝.

查看试题解析
15. 如若 $x^{2} + x = 1$ ，则 $x^{4} + x^{3} + x + 1$ 的值为.

查看试题解析
16. 如图两条相交直线y₁与y₂的图象如图所示，当x时，y₁＜y₂.

查看试题解析
17. 如图，AD是⊙O的直径， $\overset{⌢}{A B}$ ＝ $\overset{⌢}{C D}$ ，若∠AOB＝36°，则圆周角∠BPC的度数是.

查看试题解析
18. 如图，点P（3a，a）是反比例函数 $y = \frac{k}{x}$ （k＞0）与⊙O的一个交点，图中阴影部分的面积为10π，则反比例函数的表达式为.

查看试题解析

三、解答题

19. 计算： ${(- 1)}^{2021} + \sqrt{12} - 2 \tan 60^{\circ}$ .

查看试题解析
20. 先化简，再求值： $\frac{2}{a - 1} \div \frac{2 a - 4}{a^{2} - 1} - \frac{a}{a - 2}$ ，其中 $a = \sqrt{5} + 2$ ．

查看试题解析
21. 如图，四边形 $A B C D$ 是矩形，E是 $B C$ 边上一点，点F在 $B C$ 的延长线上，且 $C F = B E$ .

(1)、求证：四边形 $A E F D$ 是平行四边形；

(2)、连接 $E D$ ，若 $∠ A E D = 90 °$ ， $A B = 4$ ， $B E = 2$ ，求四边形 $A E F D$ 的面积.

查看试题解析
22. 下图为某单位地下停车库入口处的平面示意图，如图，在司机开车经过坡面即将进入车库时，在车库入口CD的上方BC处会看到一个醒目的限高标志，现已知图中BC高度为0.5m，AB宽度为9m，坡面的坡角为30°.

(1)、根据图（1）求出入口处顶点C到坡面的垂直高度CD

(2)、图（2）中，线段CE为顶点C到坡面AD的垂直距离，现已知某货车高度为3.9米，请判断该车能否进入该车库停车？（ $\sqrt{3} \approx 1.7$ ，精确到0.1米）

查看试题解析
23. 某市为了增强学生体质，全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.某中学为了了解学生对不同口味牛奶的喜好，对全校订购牛奶的学生进行了随机调查（每盒各种口味牛奶的体积相同），绘制了如图两张不完整的人数统计图：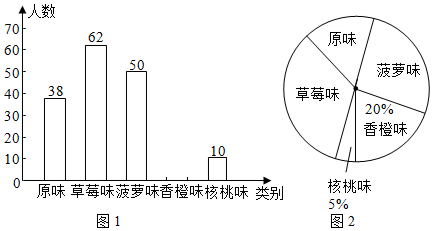

(1)、本次被调查的学生有名；

(2)、补全上面的条形统计图1；

(3)、计算喜好“菠萝味”牛奶的学生人数在扇形统计图2中所占圆心角的度数；

(4)、该校共有1200名学生订购了该品牌的牛奶，牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶，牛奶供应商每天送往该校的牛奶中，草莓味要比原味多送多少盒？

查看试题解析
24. 如图，AB为⊙O的直径，C、D为⊙O上的两个点， $\overset{⌢}{AC}$ ＝ $\overset{⌢}{C D}$ ＝ $\overset{⌢}{D B}$ ，连接AD ，过点D作DE⊥AC交AC的延长线于点E ．

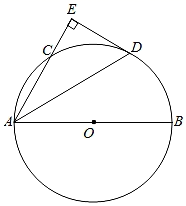(1)、求证：DE是⊙O的切线．

(2)、若直径AB＝6，求AD的长．

查看试题解析
25. 如图，矩形OABC的顶点A，C分别落在x轴，y轴的正半轴上，顶点B（2， $2 \sqrt{3}$ ），反比例函数 $y = \frac{k}{x}$ （x＞0）的图象与BC，AB分别交于D，E，BD＝ $\frac{1}{2}$ .

(1)、写出D点坐标，并求出反比例函数关系式；

(2)、判断线段DE与AC的位置关系并说明理由；

(3)、点F在直线AC上，点G是坐标系内点，当四边形BCFG为菱形时，求出点G的坐标并判断点G是否在反比例函数图象上.

查看试题解析
26. 如图，在平面直角坐标系中，抛物线y＝ax²+bx+3（a≠0）与x轴交于点A（﹣1，0）、B（3，0），与y轴交于点C，点P是直线BC上方抛物线上的动点.

(1)、求抛物线的解析式；

(2)、如图①，连接BC与OP，交于点D，求当 $\frac{P D}{O D}$ 的值最大时点P的坐标；

(3)、如图②，过点P作PD//AC交x轴于点D，交BC于点E，求 $\sqrt{10} P E - \sqrt{2}$ BE的最大值及点P的坐标.

查看试题解析