湖南省长沙市雅礼教育集团2021年数学中考模拟试卷

试卷更新日期：2021-06-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列实数中，为有理数的是（）

A、 $\sqrt{5}$ B、 $\sqrt[3]{2}$ C、1 D、 $π$

查看试题解析
2. 某几何体的三视图如图所示，这个几何体是（）

A、长方体 B、正三棱柱 C、球 D、圆柱

查看试题解析
3. 2021年，“网红城市”长沙入围“五一黄金周十大热门旅游城市”.据统计，5月1日至5日，长沙13个主要景区接待游客约1510 000人次.将1510 000用科学记数法表示应为（）

A、 1.51×10⁶ B、1.51×10⁷ C、151×10⁴ D、15.1×10⁵

查看试题解析
4. 下列说法正确的是（　　）

A、“明天的降水概率是80%”表示明天会有80%的地方下雨 B、为了解学生视力情况，抽取了500名学生进行调查，其中的样本是500名学生 C、要了解我市旅游景点客流量的情况，采用普查的调查方式 D、一组数据5，1，3，6，9的中位数是5

查看试题解析
5. 如图，河堤横断面迎水坡AB的坡比是1： $\sqrt{3}$ ，堤高BC=2米，则迎水坡宽度AC的长为（）

A、4米 B、 $2 \sqrt{3}$ 米 C、 $\frac{4}{3} \sqrt{3}$ 米 D、 $2 \sqrt{2}$ 米

查看试题解析
6. 已知关于x的一元二次方程 $x^{2} - (2 m - 1) x + m^{2} = 0$ 有实数根，则m的取值范围是（）

A、 $m \neq 0$ B、 $m \leq \frac{1}{4}$ C、 $m < \frac{1}{4}$ D、 $m > \frac{1}{4}$

查看试题解析
7. 如图，直线a∥b，直线c与直线a，b分别交于A，B两点，AC⊥AB于点A，交直线b于点C，如果∠1＝58°，那么∠2的度数为（）

A、32° B、42° C、58° D、122°

查看试题解析
8. 我国元朝数学家朱世杰的数学著作《四元玉鉴》中有一个“二果问价”问题，原题如下：“九百九十九文钱，甜果、苦果买一千，甜果九个十一文，苦果七个四文钱，试问甜苦果几个；”其大意为：用999文钱，可以买甜果和苦果共1000个，买9个甜果需要11文钱，买7个苦果需要4文钱，问买甜果和苦果的数量各多少个？设买甜果、苦果的数量分别为 $x$ 个、 $y$ 个，则可列方程组为（）

A、 ${\begin{array}{l} x + y = 999 \\ \frac{11}{9} x + \frac{4}{7} y = 1000 \end{array}$ B、 ${\begin{array}{l} x + y = 999 \\ \frac{9}{11} x + \frac{7}{4} y = 1000 \end{array}$ C、 ${\begin{array}{l} x + y = 1000 \\ \frac{11}{9} x + \frac{4}{7} y = 999 \end{array}$ D、 ${\begin{array}{l} x + y = 1000 \\ \frac{9}{11} x + \frac{7}{4} y = 999 \end{array}$

查看试题解析
9. 下列关于二次函数 $y = 2 {(x - 3)}^{2} - 5$ 的说法，正确的是（）

A、对称轴是直线 $x = - 3$ B、当 $x = 3$ 时有最小值-5 C、顶点坐标是（3，5） D、当 $x > 3$ 时，y随x的增大而减小

查看试题解析
10. 如图，正方形ABCD的边长为4，点E，点F分别是边BC，边CD上的动点，且BE=CF，AE与BF相交于点P.若点M为边BC的中点，点N为边CD上任意一点，则MN+PN的最小值等于（）

A、 $\sqrt{10} - 1$ B、5 C、 $2 \sqrt{10} - 2$ D、 $\frac{9}{2}$

查看试题解析

二、填空题

11. 计算： $\sqrt{8} - \sqrt{2}$ = ．

查看试题解析
12. 如图，为了美化校园，学校在一块靠墙角的空地上建造了一个扇形花圃，其圆心角AOB=120°，半径为6m，则扇形的弧长是m.（结果保留π）

查看试题解析
13. 某电视机制造商2021年一月份生产电视机2000台，2021年三月份生产电视机2420台，设二、三月份每月的平均增长率为x，根据题意，可列方程为.

查看试题解析
14. 已知 $a b = - 4$ ， $a + b = 2$ ，则 $a^{2} b + a b^{2}$ 的值为.

查看试题解析
15. 《九章算术》中记载了一种测量井深的方法.如图所示，在井口B处立一根垂直于井口的木杆BD，从木杆的顶端D观察井水水岸C，视线DC与井口的直径AB交于点E，如果测得AB＝1.8米，BD＝1米，BE＝0.2米，那么井深AC为米.

查看试题解析
16. 如图，直线 $y = \frac{5}{6} x - 5$ 与x轴交于点B，与双曲线 $y = \frac{k}{x}$ （ $x > 0$ ）交于点A，过点B作x轴的垂线，与双曲线 $y = \frac{k}{x}$ （ $x > 0$ ）交于点C，且AB=AC，则k的值为.

查看试题解析

三、解答题

17. 计算： $| 1 - \sqrt{3} | + {(2021 + π)}^{0} - 2 \cos 30 ° + {(- \frac{1}{2})}^{- 1}$

查看试题解析
18. 解不等式组： ${\begin{matrix} \end{matrix} \begin{matrix} 2 x + 1 > x \\ \frac{x + 5}{2} - x \geq 1 \end{matrix}$ ，并把解集在数轴上表示出来．

查看试题解析
19. 如图，直线MN∥PQ，直线AB分别与MN，PQ相交于点A，B.

(1)、利用尺规作∠NAB的平分线与PQ交于点C；

(2)、若∠ABP=70°，求∠ACB的度数.

查看试题解析
20. 随着信息技术的迅猛发展，人们去商场购物的支付方式更加多样，便捷.某校数学兴趣小组设计了一份调查问卷，要求每人选且只选种你最喜欢的支付方式，现将调查结果进行统计并绘制成两幅不完整的统计图，请结合图中所给的信息解答下列问题：

(1)、这次活动共调查了人；在扇形统计图中，表示“支付宝”支付的扇形圆心角的度数为；

(2)、将条形统计图补充完整；

(3)、如果某个社区共有3600个人，那么选择其他支付的人约有多少？

(4)、在一次购物中，小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式，请用画树状图或列表格的方法，求出两人恰好选择同一种支付方式的概率.

查看试题解析
21.
如图，E是▱ABCD的边CD的中点，延长AE交BC的延长线于点F．

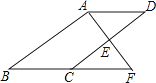(1)、求证：△ADE≌△FCE．

(2)、若∠BAF=90°，BC=5，EF=3，求CD的长．

查看试题解析
22. 为提升青少年的身体素质，某市在全市中小学推行“阳光体育”活动，某实验中学为满足学生的需求，准备再购买一些篮球和足球.如果分别用800元购买篮球和足球，购买篮球的个数比足球的个数少2个，已知足球的单价为篮球单价的 $\frac{4}{5}$ .

(1)、求篮球、足球的单价分别为多少元？

(2)、学校计划购买篮球、足球共80个，如果购买足球m个，总费用为w元，请写出w与m的函数关系式；

(3)、在（2）的条件下学校计划总费用不多于7200元，并且要求篮球数量不能低于15个，那么应如何安排购买方案才能使费用最少，最少费用应为多少？

查看试题解析
23. 如图，在Rt△ABC中，∠ACB=90°，D为AB边上的一点，以AD为直径的⊙O交BC于点E，过点C作CG⊥AB交AB于点G，交AE于点F，过点E作EP⊥AB交AB于点P，∠EAD=∠DEB.

(1)、求证：BC是⊙O的切线；

(2)、连接FP，试猜想四边形CFPE的形状，并加以证明；

(3)、若 $\sin ∠ A B C = \frac{3}{5}$ ，AC=20，求四边形CFPE的面积.

查看试题解析
24. 定义：对于给定函数 $y = a x^{2} + b x + c$ （其中a，b，c为常数，且 $a \neq 0$ ），则称函数 $y = {\begin{array}{l} a x^{2} + b x + c ， (x \geq 0) \\ a x^{2} - b x - c ， (x < 0) \end{array}$ 为函数 $y = a x^{2} + b x + c$ （其中a，b，c为常数，且 $a \neq 0$ ）的“相依函数”，此“相依函数”的图象记为G.

(1)、已知函数 $y = - x^{2} + 2 x - 1$ .
①写出这个函数的“相依函数”；

②当 $- 1 \leq x \leq 1$ 时，此相依函数的最大值为；

(2)、若直线 $y = m$ 与函数 $y = - x^{2} + 2 x - 1$ 的相依函数的图象G恰好有两个公共点，求出m的取值范围；

(3)、设函数 $y = - \frac{1}{2} x^{2} + n x + 1$ $(n > 0)$ 的相依函数的图象G在 $- 4 \leq x \leq 2$ 上的最高点的纵坐标为 $y_{0}$ ，当 $\frac{3}{2} \leq y_{0} \leq 9$ 时，求出n的取值范围.

查看试题解析
25. 已知抛物线 $y = a x^{2} + b x + c$ （ $a \neq 0$ ）与x轴分别交于点A（1，0）、点B（3，0），交y轴于点C（0， $\frac{3}{4}$ ）.

(1)、求该抛物线的函数解析式；

(2)、如图1，连接BC，取BC中点Q，连接AQ并延长交抛物线于点D，在直线AD下方的抛物线上是否存在点P，使S_△ADP=5，若存在，请求出点P的坐标，若不存在，请说明理由；

(3)、如图2，E、F是对称轴右侧第一象限抛物线上的两点，直线AE、AF分别交y轴于M、N两点，若OM·ON= $\frac{1}{4}$ ，求证：直线 EF必经过一定点.

查看试题解析