湖南省长沙市开福区十校2021年初中学生学业水平联考数学试卷

试卷更新日期：2021-06-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、（a+b）²＝a²+b² B、 $2 \sqrt{3} - \sqrt{3} = 1$ C、（a²）³＝a⁶ D、a⁴÷a⁴＝0

查看试题解析
2. 2018年我市财政计划安排社会保障和公共卫生等支出约1800000000元支持民生幸福工程，数1800000000用科学记数法表示为 $($ $)$

A、 $18 \times 10^{8}$ B、 $1.8 \times 10^{8}$ C、 $1.8 \times 10^{9}$ D、 $0.18 \times 10^{10}$

查看试题解析
3. 下列说法正确的是（）

A、“明天降雨的概率为50%”，意味着明天一定有半天都在降雨 B、了解全国快递包裹产生的包装垃圾数量适合采用全面调查（普查）方式 C、反复抛一枚均匀硬币，平均每100次出现正面朝上50次 D、一组数据的方差越小，则这组数据的波动也越小

查看试题解析
4. 若一个圆锥的母线长为6cm ，它的侧面展开图是半圆，则这个圆锥的底面半径为（）

A、1cm B、2cm C、3cm D、6cm

查看试题解析
5. 如图，用直尺和圆规作图，以点O为圆心，适当长为半径画弧，分别交OB，OA于点E、D，再分别以点E、D为圆心，大于 $\frac{1}{2}$ ED的长为半径画弧，两弧交于点C，连接OC，则△ODC≌OEC的理由是（）

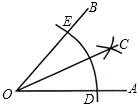A、SSS B、SAS C、AAS D、HL

查看试题解析
6. 如图，AC是电线杆AB的一根拉线，测得BC的长为6米，∠ACB=50°，则拉线AC的长为（）

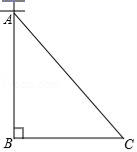A、 $\frac{6}{\sin 50^{\circ}}$ B、 $\frac{6}{\cos 50^{\circ}}$ C、6cos50° D、 $\frac{6}{\tan 50^{\circ}}$

查看试题解析
7. 下列命题错误的是（）

A、对角线互相平分的四边形是平行四边形 B、对角线相等的平行四边形是矩形 C、一条对角线平分一组对角的四边形是菱形 D、对角线互相垂直的矩形是正方形

查看试题解析
8. 如图所给的三视图表示的几何体是（）

A、长方体 B、圆柱 C、圆锥 D、圆台

查看试题解析
9. 一副直角三角板如图放置，其中 $∠ C = ∠ D F E = 90^{\circ}$ ， $∠ A = 45 °$ ， $∠ E = 60 °$ ，点F在CB的延长线上若 $D E / / C F$ ，则 $∠ B D F$ 等于（）

A、35° B、25° C、30° D、15°

查看试题解析
10. 在《九章算术》中有“盈不足术”的问题，原文如下：今有共买物，人出八，盈三；人出七，不足四，问人数几何？大意为：现有一些人共同买一个物品，每人出8元，还盈余3元；每人出7元，还差4元，问人数是多少？若设人数为 $x$ 人，则下列关于 $x$ 的方程符合题意的是（）

A、 $8 x - 3 = 7 x + 4$ B、 $8 (x - 3) = 7 (x + 4)$ C、 $8 x + 4 = 7 x - 3$ D、 $\frac{1}{7} x - 3 = \frac{1}{8} x + 4$

查看试题解析
11. 如图，是抛物线 $y_{1} = a x^{2} + b x + c$ （ $a \neq 0$ ）图象的一部分，抛物线的顶点坐标是A（1，3），与x轴的一个交点B（4，0），直线 $y_{2} = m x + n$ （ $m \neq 0$ ）与抛物线交于A，B两点，下列结论：① $2 a + b = 0$ ； ②抛物线与x轴的另一个交点是（ $- 2$ ，0）；③方程 $a x^{2} + b x + c = 3$ 有两个相等的实数根；④当时 $1 < x < 4$ ，有 $y_{2} < y_{1}$ ；⑤若 $a x_{1}^{2} + b x_{1} = a x_{2}^{2} + b x^{2}$ ，且 $x_{1} \neq x_{2}$ ；则 $x_{1} + x_{2} = 1$ .则命题正确的个数为（）

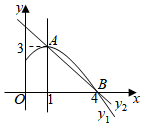A、5个 B、4个 C、3个 D、2个

查看试题解析

二、填空题

12. 将多项式 $2 x^{2} - 6 x y$ 因式分解为.

查看试题解析
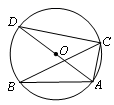
13. 在函数y＝ $\frac{\sqrt{x - 3}}{x - 4}$ 中，自变量x的取值范围是.

查看试题解析
14. 如图，△ABC内接于⊙O，AD是⊙O的直径，∠ABC＝25°，则∠CAD的度数为.

查看试题解析
15. 如图，将半径为2cm的圆形纸片折叠后，圆弧恰好经过圆心，则折痕AB的长为.

查看试题解析

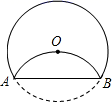
三、解答题

16. 计算： $| 1 - \sqrt{3} | - {(- 1)}^{2021} + {(π - 2021)}^{0} + {(- \frac{1}{2})}^{- 1}$

查看试题解析
17. 先化简，再求值： $(\frac{a - b}{a}) \div (a - \frac{2 a b - b^{2}}{a})$ ，其中a=3，b=1.

查看试题解析
18.
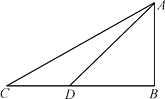
如图，某校数学兴趣小组为测得校园里旗杆AB的高度，在操场的平地上选择一点C，测得旗杆顶端A的仰角为30º，再向旗杆的方向前进16米，到达点D处(C，D，B三点在同一直线上)，又测得旗杆顶端A的仰角为45º，请计算旗杆AB的高度(结果保留根号) ．

查看试题解析
19. 为了认真贯彻教育部关于与开展“阳光体育”活动的文件精神，实施全国亿万学生每天集体锻炼一小时活动，吸引同学们走向操场、走进大自然、走到阳光下，积极参加体育锻炼，掀起校园内体育锻炼热潮，我市各学校结合实际情况举办了“阳光体育”系列活动，为了解“阳光体育”活动的落实情况，我市教育部门在红旗中学2000名学生中，随机抽取了若干名学生进行问卷调查（要求每位学生只能填写一种自己喜欢的活动），并将调查结果绘制成如下两幅不完整的统计图.

根据以上信息，解答下列问题：

(1)、参加调查的人数共有人，在扇形统计图中，表示“C”的扇形的圆心角为度；

(2)、补全条形统计图，并计算扇形统计图中m的值；

(3)、若要从该校喜欢“D”项目的学生中随机选择8名进行节目排练，则喜欢该项目的小丽同学被选中的概率是多少

查看试题解析
20. 如图，在△ABC中，∠ABC=90°，D是边AC上的一点，连接BD，使∠A=2∠1，E是BC上的一点，以BE为直径的⊙O经过点D．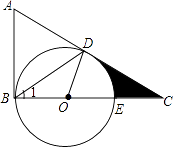

(1)、求证：AC是⊙O的切线；

(2)、若∠A=60°，⊙O的半径为2，求阴影部分的面积．（结果保留根号和π）

查看试题解析
21. 某电脑公司经销甲种型号电脑，受经济危机影响，电脑价格不断下降.今年三月份的电脑售价比去年同期每台降价1000元，如果卖出相同数量的电脑，去年销售额为10万元，今年销售额只有8万元.

(1)、今年三月份甲种电脑每台售价多少元？

(2)、为了增加收入，电脑公司决定再经销乙种型号电脑，已知甲种电脑每台进价为3500元，乙种电脑每台进价为3000元，公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台，有几种进货方案？

(3)、如果乙种电脑每台售价为3800元，为打开乙种电脑的销路，公司决定每售出一台乙种电脑，返还顾客现金 $a$ 元，要使（2）中所有方案获利相同， $a$ 值应是多少？此时，哪种方案对公司更有利？

查看试题解析
22. 如图，在四边形ABCD中，∠ABC=90°，AB=BC=BD= $\sqrt{2}$ ，BE⊥AD，BF⊥CD，垂足为E，F，AC交BF，BE分别于点G，H.

(1)、求∠EBF的度数；

(2)、求证：△ABG∽△CHB；

(3)、若CG= $\frac{1}{2}$ ，求tan∠HGB的值.

查看试题解析
23. 定义：对于给定的两个函数,任取自变量x的一个值,当x<0时,它们对应的函数值互为相反数;当x⩾0时,它们对应的函数值相等,我们称这样的两个函数互为相关函数。例如：一次函数y=x−1,它们的相关函数为y= ${\begin{cases} - x + 1 (x < 0) \\ x - 1 (x ⩾ 0) \end{cases}$ .

(1)、已知点A(−5,8)在一次函数y=ax−3的相关函数的图象上，求a的值；

(2)、已知二次函数y=−x $^{2}$ +4x− $\frac{1}{2}$ .
①当点B(m, $\frac{3}{2}$ )在这个函数的相关函数的图象上时，求m的值；

②当−3⩽x⩽3时,求函数y=−x $^{2}$ +4x− $\frac{1}{2}$ 的相关函数的最大值和最小值.

查看试题解析
24. 如图1，二次函数y＝ax²﹣2ax﹣3a（a＜0）的图象与x轴交于A、B两点（点A在点B的右侧），与y轴的正半轴交于点C，顶点为D.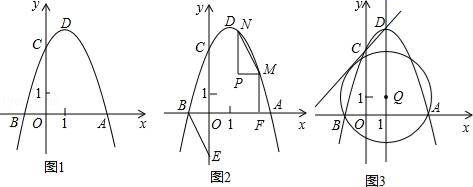

(1)、求顶点D的坐标（用含a的代数式表示）；

(2)、若以AD为直径的圆经过点C.
①求抛物线的函数关系式；

②如图2，点E是y轴负半轴上一点，连接BE，将△OBE绕平面内某一点旋转180°，得到△PMN（点P、M、N分别和点O、B、E对应），并且点M、N都在抛物线上，作MF⊥x轴于点F，若线段MF：BF＝1：2，求点M、N的坐标；

③点Q在抛物线的对称轴上，以Q为圆心的圆过A、B两点，并且和直线CD相切，如图3，求点Q的坐标.

查看试题解析