湖南省常德市安乡县2021年数学中考一模试卷

试卷更新日期：2021-06-25 类型：中考模拟

进入出卷网下载

一、单选题

1. “瓦当”是中国古建筑装饰檐头的附件，是中国特有的文化艺术遗产，下面“瓦当”图案中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列等式成立的是（）

A、 $2 a^{3} \cdot 3 a^{2} = 6 a^{5}$ B、 $a^{8} + a^{4} = a^{2} (a \neq 0)$ C、 ${(a - b)}^{2} = a^{2} - b^{2}$ D、 ${(- a^{2})}^{3} = a^{6}$

查看试题解析
3. 实数a、b、c、d在数轴上的对应点的位置如图所示，在这四个数中，绝对值最小的数是（）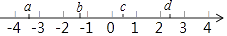

A、a B、b C、c D、d

查看试题解析
4. 已知蓄电池的电压为定值，使用蓄电池时，电流I(单位：A)与电阻R(单位：Ω)是反比例函数关系，它的图象如图所示．则用电阻R表示电流I的函数表达式为（）

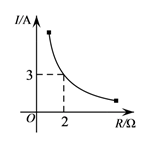A、 $I = \frac{3}{R}$ B、 $I = - \frac{6}{R}$ C、 $I = - \frac{3}{R}$ D、 $I = \frac{6}{R}$

查看试题解析
5. 测试五位学生的“ $1000$ 米”跑成绩，得到五个各不相同的数据，在统计时，出现了一处错误：将跑的最快一名学生成绩写得更快了，则计算结果不受影响的是（）

A、总成绩 B、方差 C、中位数 D、平均数

查看试题解析
6. 关于 $x$ 的一元二次方程 $k x^{2} - 6 x + 3 = 0$ 有实根，则 $k$ 的取值范围是（）

A、 $k < 3$ B、 $k < 3$ 且 $k \neq 0$ C、 $k \leq 3$ D、 $k \leq 3$ 且 $k \neq 0$

查看试题解析
7. 拦水坝横断面如图所示，迎水坡 $A B$ 的坡度（坡的竖直高度与水平宽度的比）是 $1 ： \sqrt{3}$ ，坝高 $B C = 10 m$ ，则坡面 $A B$ 的长度是（）

A、 $15 m$ B、 $20 \sqrt{3} m$ C、 $10 \sqrt{3} m$ D、 $20 m$

查看试题解析
8. 如图1，点P从△ABC的顶点A出发，沿A﹣B﹣C匀速运动，到点C停止运动.点P运动时，线段AP的长度y与运动时间x的函数关系如图2所示，其中D为曲线部分的最低点，则△ABC的面积是（）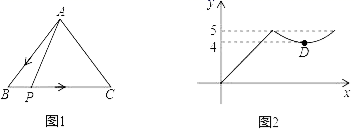

A、10 B、12 C、20 D、24

查看试题解析

二、填空题

9. 若分式 $\frac{1}{x}$ 有意义，则x的取值范围是.

查看试题解析
10. $27$ 的立方根是．

查看试题解析
11. 在国家“一带一路”战略下，我国与欧洲开通了互利互惠的中欧班列，行程最长，途经城市和国家最多的一趟专列全程长 $13000000 m$ ，将 $13000000$ 用科学记数法表示应为.

查看试题解析
12. 如图， $⊙ O$ 是 $Δ A B C$ 的外接圆，若 $∠ A B C = 35 °$ ，则 $∠ A O C$ 的度数为.

查看试题解析
13. 从 $0$ ， $π$ ， $\sqrt{2}$ ， $3.14159$ 这 $4$ 个数中选一个数，选出的这个数是无理数的概率为.

查看试题解析
14. 如图，在平行四边形ABCD中，AB=3，AD=4 $\sqrt{2}$ ，AF交BC于E，交DC的延长线于F，且CF=1，则CE的长为．

查看试题解析

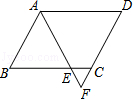15. 某校初一年级68名师生参加社会实践活动，计划租车前往，租车收费标准如下：

车型

大巴车

（最多可坐55人）

中巴车

（最多可坐39人）

小巴车

（最多可坐26人）

每车租金

（元∕天）

900

800

550

则租车一天的最低费用为元.

查看试题解析

16. 观察下列等式：
第1层 $1 + 2 = 3$

第2层 $4 + 5 + 6 = 7 + 8$

第3层 $9 + 10 + 11 + 12 = 13 + 14 + 15$

第4层 $16 + 17 + 18 + 19 + 20 = 21 + 22 + 23 + 24$

……

在上述数字宝塔中，从上往下数，2021在第层.

查看试题解析

三、解答题

17. 计算： $| 1 - \sqrt{2} | - {(\frac{1}{2})}^{- 1} - \sqrt{8} + \tan^{2} 60 °$ .

查看试题解析
18. 解不等式组： ${\begin{matrix} 5 (x - 2) \leq 3 x + 6 \\ \frac{x - 5}{2} < 1 + 4 x \end{matrix}$ ．

查看试题解析
19. 先化简再求值： $(1 - \frac{1}{x^{2} - 2 x + 1}) \div (\frac{x^{2} - 2}{x - 1} - 2)$ ，其中 $x = \sqrt{2} + 1$ .

查看试题解析
20. 如图，一次函数的图象与反比例函数的图象交于点A﹙-2，-5﹚，C﹙5，n﹚，交y轴于点B，交x轴于点D.

(1)、求反比例函数 $y = \frac{m}{x}$ 和一次函数 $y = k x + b$ 的表达式；

(2)、连接OA，OC.求△AOC的面积.

查看试题解析
21.
某日，正在我国南海海域作业的一艘大型渔船突然发生险情，相关部门接到求救信号后，立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援．当飞机到达距离海面3000米的高空C处，测得A处渔政船的俯角为60°，测得B处发生险情渔船的俯角为30°，请问：此时渔政船和渔船相距多远？（结果保留根号）

查看试题解析
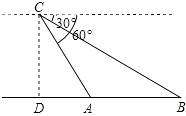22. 甲、乙两人进行摸牌游戏．现有三张形状大小完全相同的牌，正面分别标有数字2，3，5．将三张牌背面朝上，洗匀后放在桌子上．

(1)、甲从中随机抽取一张牌，记录数字后放回洗匀，乙再随机抽取一张．请用列表法或画树状图的方法，求两人抽取相同数字的概率；

(2)、若两人抽取的数字和为2的倍数，则甲获胜；若抽取的数字和为5的倍数，则乙获胜．这个游戏公平吗？请用概率的知识加以解释．

查看试题解析
23. 机械加工需要用油进行润滑以减小摩擦，某企业加工一台大型机械设备润滑用油量为90千克，用油的重复利用率为60%，按此计算，加工一台大型机械设备的实际耗油量为36千克，为了建设节约型社会，减少油耗，该企业的甲、乙两个车间都组织了人员为减少实际耗油量进行攻关.

(1)、甲车间通过技术革新后，加工一台大型机械设备润滑用油量下降到70千克，用油量的重复利用率仍然为60%.问甲车间技术革新后，加工一台大型机械设备的实际耗油量是多少千克？

(2)、乙车间通过技术革新后，不仅降低了润滑用油量，同时也提高了用油的重复利用率，并且发现在技术革新前的基础上，润滑用油量每减少1千克，用油的重复利用率将增加1.6%，这样乙车间加工一台大型机械设备的实际耗油量下降到12千克，问乙车间技术革新后，加工一台大型机械设备的润滑用油量是多少千克？用油的重复利用率是多少？

查看试题解析
24. 如图， $A B$ 是 $⊙ O$ 的直径， $C$ 是 $⊙ O$ 上一点，直线 $M N$ 经过点 $C$ ，过点 $A$ 作直线 $M N$ 的垂线，垂足为点 $D$ ，且 $A C$ 平分 $∠ B A D$ .

(1)、求证：直线 $M N$ 是 $⊙ O$ 的切线；

(2)、若 $C D = 3$ ， $A C = 5$ ，求 $⊙ O$ 的直径.

查看试题解析
25. 如图，抛物线y＝ax²+2x+c（a＜0）与x轴交于点A和点B（点A在原点的左侧，点B在原点的右侧），与y轴交于点C ， OB＝OC＝3．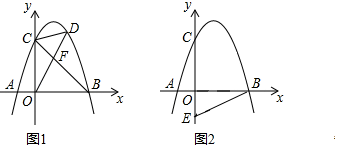

(1)、求该抛物线的函数解析式；

(2)、如图1，连接BC ，点D是直线BC上方抛物线上的点，连接OD ， CD ， OD交BC于点F ，当S_△COF：S_△CDF＝3：2时，求点D的坐标．

(3)、如图2，点E的坐标为（0， $- \frac{3}{2}$ ），在抛物线上是否存在点P ，使∠OBP＝2∠OBE？若存在，请直接写出符合条件的点P的坐标；若不存在，请说明理由．

查看试题解析
26. 如图， $Δ A D E$ 由 $Δ A B C$ 绕点 $A$ 按逆时针方向旋转 $90 °$ 得到，且点 $B$ 的对应点D恰好落在 $B C$ 的延长线上， $A D$ ， $E C$ 相交于点 $P$ ．

(1)、求 $∠ B D E$ 的度数；

(2)、 $F$ 是 $E C$ 延长线上的点，且 $∠ C D F = ∠ D A C$ ．
①判断 $D F$ 和 $P F$ 的数量关系，并证明；

②求证： $\frac{E P}{P F} = \frac{P C}{C F}$ ．

查看试题解析