湖北省襄阳市樊城区2021年数学中考适应性卷
试卷更新日期:2021-06-25 类型:期中考试
一、单选题
-
1. 下列各数中,比-4小的数是( )A、-2.5 B、-5 C、0 D、22. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )A、
 赵爽弦图
B、
赵爽弦图
B、 笛卡尔心形线
C、
笛卡尔心形线
C、 科克曲线
D、
科克曲线
D、 斐波那契螺旋线
3. 下列各式中,运算正确的是( )A、 B、 C、 D、4. 我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.如图所示的几何体是可以形成“牟合方盖”的一种模型,它的俯视图是( )
斐波那契螺旋线
3. 下列各式中,运算正确的是( )A、 B、 C、 D、4. 我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.如图所示的几何体是可以形成“牟合方盖”的一种模型,它的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 如图所示,直线 , , ,则 的大小是( )
5. 如图所示,直线 , , ,则 的大小是( ) A、73° B、83° C、77° D、87°6. 某商场一月份的营业额为400万元,第一季度营业总额为1600万元,若平均每月增长率为x,则可列方程为( )A、400(1+x)2=1600 B、400[1+(1+x)+(1+x)2]=1600 C、400+400x+400x2=1600 D、400(1+x+2x)=16007. 下列说法正确的是( )A、“连接一个菱形的两条对角线,它们互相垂直平分”这一事件是随机事件. B、概率很小的事件不可能发生. C、367人中一定至少有两个人同一天生日. D、“明天降雨的概率为80%”,意味着明天有80%的时间会有降雨.8. 如图,A,B,C是3×1的正方形网格中的三个格点,则 tan∠ABC的值为( )
A、73° B、83° C、77° D、87°6. 某商场一月份的营业额为400万元,第一季度营业总额为1600万元,若平均每月增长率为x,则可列方程为( )A、400(1+x)2=1600 B、400[1+(1+x)+(1+x)2]=1600 C、400+400x+400x2=1600 D、400(1+x+2x)=16007. 下列说法正确的是( )A、“连接一个菱形的两条对角线,它们互相垂直平分”这一事件是随机事件. B、概率很小的事件不可能发生. C、367人中一定至少有两个人同一天生日. D、“明天降雨的概率为80%”,意味着明天有80%的时间会有降雨.8. 如图,A,B,C是3×1的正方形网格中的三个格点,则 tan∠ABC的值为( )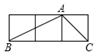 A、 B、 C、 D、9. 有一题目:“已知,点 为 的外心, ,求 .”
A、 B、 C、 D、9. 有一题目:“已知,点 为 的外心, ,求 .”嘉嘉的解答为:如图,画 以及它的外接圆 ,连接 , .由 ,得 .
淇淇说:“嘉嘉考虑的不周全, 还应有另一个不同的值.”
下列判断正确的是( )
 A、淇淇说的对,且 的另一个值是115° B、淇淇说的不对, 就得65° C、嘉嘉求的结果不对, 应得80° D、两人都不对, 应有3个不同的值10. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是( )
A、淇淇说的对,且 的另一个值是115° B、淇淇说的不对, 就得65° C、嘉嘉求的结果不对, 应得80° D、两人都不对, 应有3个不同的值10. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是( ) A、abc<0 B、b2﹣4ac<0 C、a﹣b+c<0 D、2a+b=0
A、abc<0 B、b2﹣4ac<0 C、a﹣b+c<0 D、2a+b=0二、填空题
-
11. 计算: .12. 袋中有6个黑球和n个白球,经过若干次试验,发现“若从中任意摸一个球,恰好摸到白球的概率为 ”,则这个袋中的白球大约有个.13. 为改善生态环境,避免水土流失,某村积极植树造林,原计划每天植树60棵,实际每天植树80棵,结果比预计时间提前4天完成植树任务,则植树总任务棵.14. 如图,正方形的边长为2,分别以它的四条边为直径画半圆,则阴影部分的面积为(结果保留π).
 15. 已知不等式组 有解但没有整数解,则 的取值范围为.16. 两幅大小不同的三角板中各取一个,如图1叠放(直角顶点重合), , ,且 ,把 绕点 顺时针旋转45°后, 交 于点 ,则 .
15. 已知不等式组 有解但没有整数解,则 的取值范围为.16. 两幅大小不同的三角板中各取一个,如图1叠放(直角顶点重合), , ,且 ,把 绕点 顺时针旋转45°后, 交 于点 ,则 .
三、解答题
-
17. 先化简;再求值: ;其中a= +1,b= -1.18. 《2021湖北青春与法同行知识竞赛》以学习贯彻《宪法》《民法典》《未成年人保护法》等为重点,面向全省青少年开展10期线上有奖知识竞答,某校组织七、八年级各200名学生对《知识竞赛》相关知识进行学习并组织参赛.现分别在七、八两个年级中各随机抽取了10名学生,统计这部分学生的竞赛成绩,相关数据统计、整理如下:
(收集数据)
七年级10名同学测试成绩统计如下:72,84,72,91,79,69,78,85,75,95
八年级10名同学测试成绩统计如下:85,72,92,84,80,74,75,80,76,82
(整理数据)两组数据各分数段,如下表所示:
成绩
七年级
1
5
2
八年级
0
4
5
1
(分析数据)两组数据的平均数、中位数、众数、方差如下表:
统计量年级
平均数
中位数
众数
方差
七年级
80
72
八年级
80
80
33
(问题解决)根据以上信息,解答下列问题:
(1)、填空: , , ;(2)、计算八年级同学测试成绩的方差是:.
请你求出七年级同学成绩的方差,试估计哪个年级的竞赛成绩更整齐?
(3)、按照比赛规定90分及其以上算优秀,请估计这两个年级竞赛成绩达到优秀学生的人数共有多少人?19. 小云同学根据函数的学习经验,对函数 进行探索,已知函数的图象经过点 , .(1)、填空: , ;(2)、补充表格,在平面直角坐标系中,描出表中各组值对应坐标的点,画出该函数的图象;…
-3
-2
-1
5
…
…
3
1
…
(3)、观察函数图象,下列关于函数性质的描述正确的有:;
①当 时, 随 的增大而增大;
②当 时, 随 的增大而减小;
③函数 的图象关于直线 轴对称;
④当 时,函数值 取得最大值3.
(4)、过点 作直线 平行于 轴,若直线 与函数 有两个交点,则 的取值范围是.20. 如图, 、 分别是 的边 和 上的高,点 在线段 的延长线上,且 ,点 在线段 上,且 .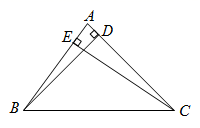 (1)、用直尺和圆规,作出点 、 的位置(不写作法,保留作图痕迹);(2)、判断线段 和 的关系?并说明理由.21. 如图1是位于襄阳城南岘首山上重建的“岘首亭”的夜景,岘首亭原名岘山亭,为纪念东晋大将羊祜而修建,唐代诗人孟浩然曾以此亭赋诗,留下了“江山留胜迹,我辈复登临.”的千古名句.某校数学兴趣小组在学完了三角函数的知识后,决定用自己学到的知识测量“岘首亭”的高度,站在岘首山对面“习家池风景区”入口 处测得亭顶 的仰角为37°,前行 ,穿过旧的207国道来到同一水平面的岘首山脚 处,测得山脚 到亭底 的坡长为 ,仰角为30°,请根据兴趣小组测得的数据,利用图2求首亭 的高度.
(1)、用直尺和圆规,作出点 、 的位置(不写作法,保留作图痕迹);(2)、判断线段 和 的关系?并说明理由.21. 如图1是位于襄阳城南岘首山上重建的“岘首亭”的夜景,岘首亭原名岘山亭,为纪念东晋大将羊祜而修建,唐代诗人孟浩然曾以此亭赋诗,留下了“江山留胜迹,我辈复登临.”的千古名句.某校数学兴趣小组在学完了三角函数的知识后,决定用自己学到的知识测量“岘首亭”的高度,站在岘首山对面“习家池风景区”入口 处测得亭顶 的仰角为37°,前行 ,穿过旧的207国道来到同一水平面的岘首山脚 处,测得山脚 到亭底 的坡长为 ,仰角为30°,请根据兴趣小组测得的数据,利用图2求首亭 的高度.(参考数据: , , , ,结果精确到 )
 22. 如图,在 中, ,以 为直径的 与边 交于点 ,过点 作 ,垂足为点 , 的反向延长线交 与点 .
22. 如图,在 中, ,以 为直径的 与边 交于点 ,过点 作 ,垂足为点 , 的反向延长线交 与点 . (1)、求证: 是 的切线;(2)、若圆的半径为10, ,求 的长.23. 2020年两会,总理点赞地摊经济,一夜之间,“地摊”成了当下的潮流,即将大学毕业的小明也准备“摆摊”磨练一下,进货时发现:8件 商品和4件 商品进货需要72元;4件 商品和3件 商品进货需要38元.(1)、则 、 每件商品的进价各是;(2)、两种商品共进货300件,设 商品购进 件( ), 商品的总售价为 元, 商品的总售价为 元,总售价 (元)与销量件数之间是一次函数关系,如下表:
(1)、求证: 是 的切线;(2)、若圆的半径为10, ,求 的长.23. 2020年两会,总理点赞地摊经济,一夜之间,“地摊”成了当下的潮流,即将大学毕业的小明也准备“摆摊”磨练一下,进货时发现:8件 商品和4件 商品进货需要72元;4件 商品和3件 商品进货需要38元.(1)、则 、 每件商品的进价各是;(2)、两种商品共进货300件,设 商品购进 件( ), 商品的总售价为 元, 商品的总售价为 元,总售价 (元)与销量件数之间是一次函数关系,如下表:件数(商品 )
0
1
2
20
30
…
(元)
0
10
20
200
300
…
总售价 (元)与销量 (件)之间的函数关系如图:
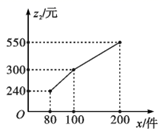
①直接写出 、 和 之间的函数关系式;
②设销售 、 两件商品所获总利润为 元,求 与 之间的函数关系式;
(3)、若将小明所进的300件 、 商品全部售完,预计共获利 ( )元,当 商品的销售量最大时,他计划每件 、 商品分别捐给学校助学基金 元和 元,捐款数恰好等于总成本的10%,求 的值.24. 在矩形 中,点 是对角线 、 的交点,直角 的顶点 与 重合, 、 分别与 、 边相交于 、 ,连接 , ( 为常数). (1)、发现问题:如图1,若 ,猜想: ;(2)、类比探究:如图2, ,探究线段 , 之间的数量关系,并说明理由;(3)、拓展运用:如图3,在(2)的条件下,若 , , ,求 的长.25. 如图,边长为5的正方形 的两边在坐标轴上,以点 为顶点的抛物线经过点 ,点 是抛物线上第一象限内一点,过 点作 于点 ,点 的坐标为 .连接 .
(1)、发现问题:如图1,若 ,猜想: ;(2)、类比探究:如图2, ,探究线段 , 之间的数量关系,并说明理由;(3)、拓展运用:如图3,在(2)的条件下,若 , , ,求 的长.25. 如图,边长为5的正方形 的两边在坐标轴上,以点 为顶点的抛物线经过点 ,点 是抛物线上第一象限内一点,过 点作 于点 ,点 的坐标为 .连接 . (1)、求抛物线的解析式;(2)、求 的值;(3)、①在点 运动过程中,当 时,点 的坐标为;
(1)、求抛物线的解析式;(2)、求 的值;(3)、①在点 运动过程中,当 时,点 的坐标为;②连接 ,在①的条件下,把 沿 轴平移(限定点 在射线 上),并使抛物线与 的边始终有两个交点,探究 点纵坐标 的取值范围是多少?