湖北省通山县2021年九年级5月教学质量监测数学试卷
试卷更新日期:2021-06-25 类型:中考模拟
一、单选题
-
1. 计算 的结果是( )A、-3 B、-1 C、1 D、32. 下列计算正确的是( )A、 B、 C、 D、3. 若一个凸多边形的内角和为720°,则这个多边形的边数为A、4 B、5 C、6 D、74. 今年端午小长假复课第一天,学校根据疫情防控要求,对所有进入校园的师生进行体温检测,其中7名学生的体温(单位: )如下:36.5,36.3,36.8,36.3,36.5,36.7,36.5,这组数据的众数和中位数分别是( )A、36.3,36.5 B、36.5,36.5 C、36.5,36.3 D、36.3,36.75. 如图是一个正五棱柱,它的俯视图是( )
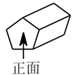 A、
A、 B、
B、 C、
C、 D、
D、 6. 已知关于 的一元二次方程 有两个相等的实数根,设两根分别为 , ,则 的值为( )A、2 B、-2 C、4 D、-47. 如图,在直径为 的半圆 中, 为半圆上一点,连接 , ,利用尺规在 , 上分别截取 , ,使 ;分别以 , 为圆心、以大于 的长为半径作弧,两弧在 内交于点 ;作射线 交 于点 .若 , , 为 上一动点,则 的最小值为( )
6. 已知关于 的一元二次方程 有两个相等的实数根,设两根分别为 , ,则 的值为( )A、2 B、-2 C、4 D、-47. 如图,在直径为 的半圆 中, 为半圆上一点,连接 , ,利用尺规在 , 上分别截取 , ,使 ;分别以 , 为圆心、以大于 的长为半径作弧,两弧在 内交于点 ;作射线 交 于点 .若 , , 为 上一动点,则 的最小值为( )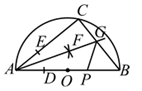 A、2 B、 C、4 D、无法确定8. 如图,点 是菱形 边上的动点,它从点 出发沿 路径匀速运动到点 ,设 的面积为 ,点 的运动时间为 ,则 关于 的函数图象大致为( )
A、2 B、 C、4 D、无法确定8. 如图,点 是菱形 边上的动点,它从点 出发沿 路径匀速运动到点 ,设 的面积为 ,点 的运动时间为 ,则 关于 的函数图象大致为( )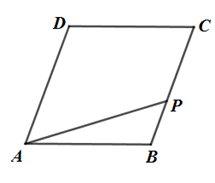 A、
A、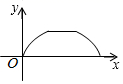 B、
B、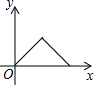 C、
C、 D、
D、
二、填空题
-
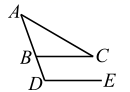
9. 如图,在 中, ,点 在 的延长线上, ,若 ,则 °.
 10. 不等式组 的解集是.11. 某校征集校运会会徽,遴选出甲、乙、丙三种图案.为了解何种图案更受欢迎,随机调查了该校100名学生,其中58名同学喜欢甲图案,若该校共有2000人,根据所学的统计知识可以估计该校喜欢甲图案的学生约有人.12. 《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”译文大致是:“用一根绳子去量一根木条,绳子剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?”如果设木条长x尺,绳子长y尺,可列方程组为;13. 如图,点 为扇形 的半径 上一点,将 沿 折叠,点 恰好落在 上的点 处,且 ,若 ,则 的长为.
10. 不等式组 的解集是.11. 某校征集校运会会徽,遴选出甲、乙、丙三种图案.为了解何种图案更受欢迎,随机调查了该校100名学生,其中58名同学喜欢甲图案,若该校共有2000人,根据所学的统计知识可以估计该校喜欢甲图案的学生约有人.12. 《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”译文大致是:“用一根绳子去量一根木条,绳子剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?”如果设木条长x尺,绳子长y尺,可列方程组为;13. 如图,点 为扇形 的半径 上一点,将 沿 折叠,点 恰好落在 上的点 处,且 ,若 ,则 的长为.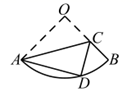 14. 二次函数 ( , , 是常数, )的自变量 与函数值 的部分对应值如表:
14. 二次函数 ( , , 是常数, )的自变量 与函数值 的部分对应值如表:…
0
1
2
…
…
…
且当 时,与其对应的函数值 ,有下列结论:① ;② 和3是关于 的方程 的两个根;③当 时, 随 的增大而增大;④ .其中所有正确结论的序号是.
三、解答题
-
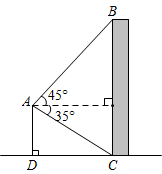
15. 如图,无人机于空中 处测得某建筑顶部 处的仰角为45°,测得该建筑底部 处的俯角为35°.若无人机的飞行高度 为42m,则该建筑的高度 为 .(参考数据: , , ).
 16. 计算: .17. A,B两种机器人都被用来搬运化工原料,A型机器人每小时搬运的化工原料是B型机器人每小时搬运的化工原料的1.5倍,A型机器人搬运 所用时间比B型机器人搬运 所用时间少1小时.两种机器人每小时分别搬运多少化工原料?18. “五一”期间,小红和小慧从隐水洞、龙隐山、石门村这3个景点中随机选择1个景点游览.(1)、小红选择的景点是隐水洞的概率是;(2)、用列表或画树状图的方法,求小红和小慧所选景点恰好相同的概率(提示:不妨把隐水洞记为A,龙隐山记为B,石门村记为C).19. 已知直线 过点 .点P为直线l上一点,其横坐标为m . 过点P作y轴的垂线,与函数 的图象交于点Q .
16. 计算: .17. A,B两种机器人都被用来搬运化工原料,A型机器人每小时搬运的化工原料是B型机器人每小时搬运的化工原料的1.5倍,A型机器人搬运 所用时间比B型机器人搬运 所用时间少1小时.两种机器人每小时分别搬运多少化工原料?18. “五一”期间,小红和小慧从隐水洞、龙隐山、石门村这3个景点中随机选择1个景点游览.(1)、小红选择的景点是隐水洞的概率是;(2)、用列表或画树状图的方法,求小红和小慧所选景点恰好相同的概率(提示:不妨把隐水洞记为A,龙隐山记为B,石门村记为C).19. 已知直线 过点 .点P为直线l上一点,其横坐标为m . 过点P作y轴的垂线,与函数 的图象交于点Q .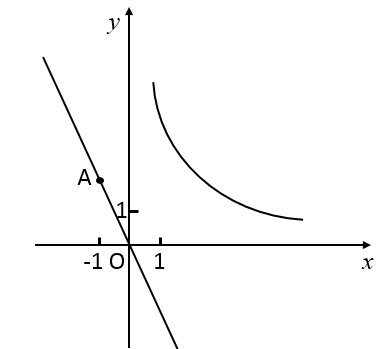 (1)、求k的值;(2)、①求点Q的坐标(用含m的式子表示);
(1)、求k的值;(2)、①求点Q的坐标(用含m的式子表示);②若 的面积大于3,直接写出点P的横坐标m的取值范围.
20. 如图,在 中, ,以 为直径的⊙ 分别交 于点 ,点 在 的延长线上,且 . (1)、求证: 是⊙ 的切线;(2)、若⊙ 的直径为3, ,求 和 的长.21. 某商店销售一种商品,童威经市场调查发现:该商品的周销售量 (件)是售价 (元/件)的一次函数,其售价、周销售量、周销售利润 (元)的三组对应值如下表:
(1)、求证: 是⊙ 的切线;(2)、若⊙ 的直径为3, ,求 和 的长.21. 某商店销售一种商品,童威经市场调查发现:该商品的周销售量 (件)是售价 (元/件)的一次函数,其售价、周销售量、周销售利润 (元)的三组对应值如下表:售价 (元/件)
50
60
80
周销售量 (件)
100
80
40
周销售利润 (元)
1000
1600
1600
注:周销售利润=周销售量×(售价-进价)
(1)、①求 关于 的函数解析式(不要求写出自变量的取值范围)②该商品进价是 ▲ 元/件;当售价是 ▲ 元/件时,周销售利润最大,最大利润是 ▲ 元
(2)、由于某种原因,该商品进价提高了 元/件 ,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求 的值22. 在 中, , .点 是 内一点.连接 ,将线段 绕点 逆时针旋转 得到线段 ,连接 , , .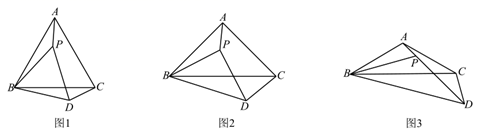 (1)、观察猜想,如图1,当 时,求 的值.(2)、类比探究,如图2,当 时,求 的值.(3)、解决问题,如图3,当 时,若点 在 的平分线上,请直接写出点 , , 在同一直线上时 与 的值.23. 二次函数 的图象与x轴交于A(2,0),B(6,0)两点,与y轴交于点C,顶点为E.
(1)、观察猜想,如图1,当 时,求 的值.(2)、类比探究,如图2,当 时,求 的值.(3)、解决问题,如图3,当 时,若点 在 的平分线上,请直接写出点 , , 在同一直线上时 与 的值.23. 二次函数 的图象与x轴交于A(2,0),B(6,0)两点,与y轴交于点C,顶点为E.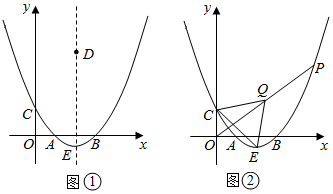 (1)、求这个二次函数的表达式,并写出点E的坐标;(2)、如图①,D是该二次函数图象的对称轴上一个动点,当BD的垂直平分线恰好经过点C时,求点D的坐标;(3)、如图②,P是该二次函数图象上的一个动点,连接OP,取OP中点Q,连接QC,QE,CE,当△CEQ的面积为12时,求点P的坐标.
(1)、求这个二次函数的表达式,并写出点E的坐标;(2)、如图①,D是该二次函数图象的对称轴上一个动点,当BD的垂直平分线恰好经过点C时,求点D的坐标;(3)、如图②,P是该二次函数图象上的一个动点,连接OP,取OP中点Q,连接QC,QE,CE,当△CEQ的面积为12时,求点P的坐标.