湖北省天门市2021年九年级下学期学业质量监测数学试卷
试卷更新日期:2021-06-25 类型:中考模拟
一、单选题
-
1. 2021的相反数是( )A、 -2021 B、 C、2021 D、2. 下列立体图形中,左视图与主视图不同的是( )A、
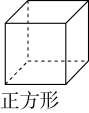 B、
B、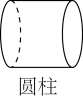 C、
C、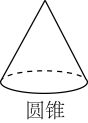 D、
D、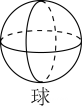 3. “扶贫”是新时期党和国家的重点工作之一,为落实习近平总书记提出的“精准扶贫”战略构想,某省预计三年内脱贫1020000人,数字1020000用科学记数法可表示为( )A、1.02×106 B、1.02×105 C、10.2×105 D、102×1044. 下列说法正确的是( )A、要了解我国中学生的视力情况应做全面调查 B、一组数据中,平均数是4,众数是3,则中位数一定是5 C、“掷一次骰子,向上一面的点数是3”是随机事件 D、甲、乙两组数据,若 ,则乙组的数据波动大5. 如图,将直尺与含30°角的三角尺叠放在一起,若∠1=40°,则∠2的大小是( )
3. “扶贫”是新时期党和国家的重点工作之一,为落实习近平总书记提出的“精准扶贫”战略构想,某省预计三年内脱贫1020000人,数字1020000用科学记数法可表示为( )A、1.02×106 B、1.02×105 C、10.2×105 D、102×1044. 下列说法正确的是( )A、要了解我国中学生的视力情况应做全面调查 B、一组数据中,平均数是4,众数是3,则中位数一定是5 C、“掷一次骰子,向上一面的点数是3”是随机事件 D、甲、乙两组数据,若 ,则乙组的数据波动大5. 如图,将直尺与含30°角的三角尺叠放在一起,若∠1=40°,则∠2的大小是( )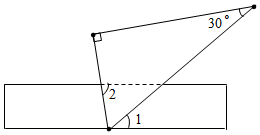 A、40° B、60° C、70° D、80°6. 不等式组 的解集在数轴上表示正确的是( )A、
A、40° B、60° C、70° D、80°6. 不等式组 的解集在数轴上表示正确的是( )A、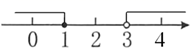 B、
B、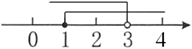 C、
C、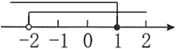 D、
D、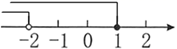 7. 如图,有一块半径为1m,圆心角为 的扇形铁皮,要把它做成一个圆锥形容器(接缝忽略不计),那么这个圆锥形容器的高为( ).
7. 如图,有一块半径为1m,圆心角为 的扇形铁皮,要把它做成一个圆锥形容器(接缝忽略不计),那么这个圆锥形容器的高为( ). A、 B、 C、 D、8. 下列语句.①横坐标与纵坐标互为相反数的点在直线y=-x上;②直线y=-x+2不经过第三象限;③除了用有序实数对,我们也可以用方向和距离来确定物体的位置;④若点P的坐标为(a,b),且ab=0,则P点是坐标原点;⑤函数 中y的值随x的增大而减小.其中叙述正确的有( )A、2个 B、3个 C、4个 D、5个9. 在同一平面直角坐标系中,若抛物线y=mx2+2x﹣n与y=﹣6x2﹣2x+m﹣n关于x轴对称,则m,n的值为( )A、m=﹣6,n=﹣3 B、m=﹣6,n=3 C、m=6,n=﹣3 D、m=6,n=310. 如图,矩形 的对角线 , 交于点 , , ,过点 作 ,交 于点 ,过点 作 ,垂足为 ,则 的值为( )
A、 B、 C、 D、8. 下列语句.①横坐标与纵坐标互为相反数的点在直线y=-x上;②直线y=-x+2不经过第三象限;③除了用有序实数对,我们也可以用方向和距离来确定物体的位置;④若点P的坐标为(a,b),且ab=0,则P点是坐标原点;⑤函数 中y的值随x的增大而减小.其中叙述正确的有( )A、2个 B、3个 C、4个 D、5个9. 在同一平面直角坐标系中,若抛物线y=mx2+2x﹣n与y=﹣6x2﹣2x+m﹣n关于x轴对称,则m,n的值为( )A、m=﹣6,n=﹣3 B、m=﹣6,n=3 C、m=6,n=﹣3 D、m=6,n=310. 如图,矩形 的对角线 , 交于点 , , ,过点 作 ,交 于点 ,过点 作 ,垂足为 ,则 的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
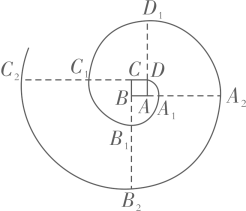
11. 分解因式: .12. 今年新冠病毒疫情初期,口罩供应短缺,某地规定:每人每次限购5只.李红出门买口罩时,无论是否买到,都会消耗家里库存的口罩一只,如果有口罩买,他将买回5只.已知李红家原有库存15只,出门10次购买后,家里现有口罩35只.请问李红出门没有买到口罩的次数是次.13. 在解一元二次方程x2+bx+c=0时,小明看错了一次项系数b,得到的解为x1=2,x2=3;小刚看错了常数项c,得到的解为x1=1,x2=5.请你写出正确的一元二次方程.14. 从长度分别为1,2,3,4的四条线段中任选3条,能构成三角形的概率为 .15. 如果三角形有一边上的中线长等于这边的长,那么称这个三角形为“好玩三角形”.若 是“好玩三角形”,且 ,则 .16. 如图,四边形 是正方形,曲线 是由一段段90度的弧组成的.其中: 的圆心为点A,半径为 ;
的圆心为点B,半径为 ;
的圆心为点C,半径为 ;
的圆心为点D,半径为 ;…
的圆心依次按点A,B,C,D循环.若正方形 的边长为1,则 的长是 .
三、解答题
-
17.(1)、计算: ;(2)、解方程: .18. 如图,平行四边形ABCD中,点E在BC上,且AE=EC,试分别在下列两个图中按要求使用无刻度直尺画图.(保留作图痕迹)
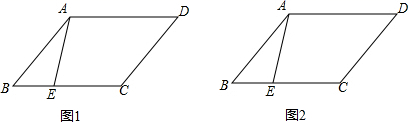 (1)、在图1中,画出∠DAE的平分线;(2)、在图2中,画出∠AEC的平分线.19. 勤劳是中华民族的传统美德,学校要求学生在家帮助父母做一些力所能及的家务.在学期初,小丽同学随机调查了七年级部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为x小时,将做家务的总时间分为五个类别:A(0≤x<10),B(10≤x<20),C(20≤x<30),D(30≤x<40),E(x≥40).并将调查结果绘制了如图两幅不完整的统计图:
(1)、在图1中,画出∠DAE的平分线;(2)、在图2中,画出∠AEC的平分线.19. 勤劳是中华民族的传统美德,学校要求学生在家帮助父母做一些力所能及的家务.在学期初,小丽同学随机调查了七年级部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为x小时,将做家务的总时间分为五个类别:A(0≤x<10),B(10≤x<20),C(20≤x<30),D(30≤x<40),E(x≥40).并将调查结果绘制了如图两幅不完整的统计图: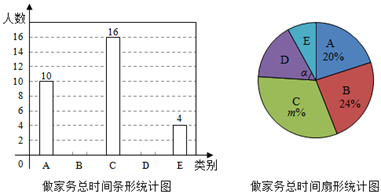
根据统计图提供的信息,解答下列问题:
(1)、本次共调查了名学生;(2)、根据以上信息直接在答题卡上补全条形统计图;(3)、扇形统计图中m= , 类别D所对应的扇形圆心角α的度数是度;(4)、若从七年级随机抽取一名学生,估计这名学生寒假在家做家务的总时间不低于20小时的概率.20. 如图, 两点的坐标分别为 ,将线段 绕点 逆时针旋转90°得到线段 ,过点 作 ,垂足为 ,反比例函数 的图象经过点 .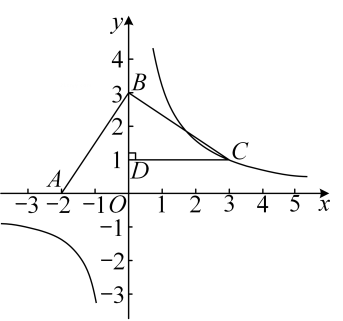 (1)、直接写出点 的坐标,并求反比例函数的解析式;(2)、点 在反比例函数 的图象上,当 的面积为3时,求点 的坐标.21. 如图,在 中,以 为直径的 交 于点 ,弦 交 于点 ,且 .
(1)、直接写出点 的坐标,并求反比例函数的解析式;(2)、点 在反比例函数 的图象上,当 的面积为3时,求点 的坐标.21. 如图,在 中,以 为直径的 交 于点 ,弦 交 于点 ,且 .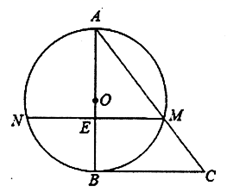 (1)、求证: 是 的切线;(2)、若 ,求 的直径 的长度.22. 随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
(1)、求证: 是 的切线;(2)、若 ,求 的直径 的长度.22. 随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
7
25
0.01
B
m
n
0.01
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA , yB.
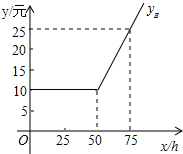 (1)、如图是yB与x之间函数关系的图象,请根据图象填空:m=;n=;(2)、写出yA与x之间的函数关系式;(3)、选择哪种方式上网学习合算,为什么.23. 如图1,矩形ABCD中,已知AB=6.BC=8,点E是射线BC上的一个动点,连接AE并延长,交射线DC于点F.将△ABE沿直线AE翻折,点B的对应点为点B′,延长AB′ 交直线CD于点M.
(1)、如图是yB与x之间函数关系的图象,请根据图象填空:m=;n=;(2)、写出yA与x之间的函数关系式;(3)、选择哪种方式上网学习合算,为什么.23. 如图1,矩形ABCD中,已知AB=6.BC=8,点E是射线BC上的一个动点,连接AE并延长,交射线DC于点F.将△ABE沿直线AE翻折,点B的对应点为点B′,延长AB′ 交直线CD于点M.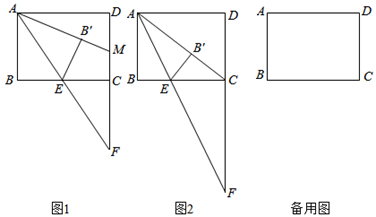 (1)、如图1,当点M在线段CD上时,求证:AM=FM;(2)、如图2,若点B′ 恰好落在对角线AC上,求 的值;(3)、若 ,求线段AM的长.24. 如图,直线 交y轴于点A,交x轴于点C,抛物线 经过点A,点C,且交x轴于另一点B.
(1)、如图1,当点M在线段CD上时,求证:AM=FM;(2)、如图2,若点B′ 恰好落在对角线AC上,求 的值;(3)、若 ,求线段AM的长.24. 如图,直线 交y轴于点A,交x轴于点C,抛物线 经过点A,点C,且交x轴于另一点B.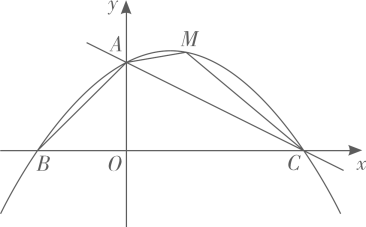 (1)、直接写出点A,点B,点C的坐标及抛物线的解析式;(2)、在直线 上方的抛物线上有一点M,求四边形 面积的最大值及此时点M的坐标;(3)、将线段 绕x轴上的动点 顺时针旋转90°得到线段 ,若线段 与抛物线只有一个公共点,请结合函数图象,求m的取值范围.
(1)、直接写出点A,点B,点C的坐标及抛物线的解析式;(2)、在直线 上方的抛物线上有一点M,求四边形 面积的最大值及此时点M的坐标;(3)、将线段 绕x轴上的动点 顺时针旋转90°得到线段 ,若线段 与抛物线只有一个公共点,请结合函数图象,求m的取值范围.