山东省临沂市罗庄区2021年中考数学一模试卷
试卷更新日期:2021-06-25 类型:中考模拟
一、单选题
-
1. 下列各数中比-2小的数是( )A、 B、 C、 D、2. 下列垃圾分类标识的图案既是轴对称图形,又是中心对称图形的是( )A、
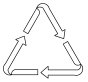 B、
B、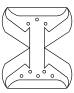 C、
C、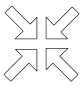 D、
D、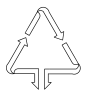 3. 一副直角三角板如图放置,使两三角板的斜边互相平行,每块三角板的直角顶点都在另一三角板的斜边上,则∠1的度数为( )
3. 一副直角三角板如图放置,使两三角板的斜边互相平行,每块三角板的直角顶点都在另一三角板的斜边上,则∠1的度数为( )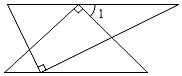 A、30° B、45° C、55° D、60°4. 下列运算正确的是( )A、 B、 C、 D、5. 下图是由4个相同的正方体组成的立体图形,它的左视图是( )
A、30° B、45° C、55° D、60°4. 下列运算正确的是( )A、 B、 C、 D、5. 下图是由4个相同的正方体组成的立体图形,它的左视图是( )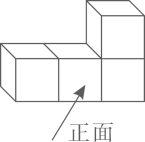 A、
A、 B、
B、 C、
C、 D、
D、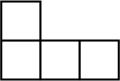 6. 如图,小球从A入口往下落,在每个交叉口都有向左或向右两种可能,且可能性相等,则小球从E出口落出的概率是( )
6. 如图,小球从A入口往下落,在每个交叉口都有向左或向右两种可能,且可能性相等,则小球从E出口落出的概率是( )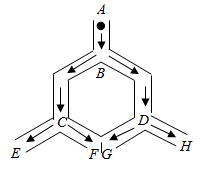 A、 B、 C、 D、7. 不等式组 的解集在数轴上表示正确的是( )A、
A、 B、 C、 D、7. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、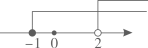 D、
D、 8. 如图,数轴上两点 所对应的实数分别为 ,则 的结果可能是( )
8. 如图,数轴上两点 所对应的实数分别为 ,则 的结果可能是( )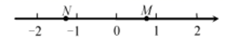 A、 B、1 C、2 D、39. 学校计划用200元钱购买 、 两种奖品, 种每个15元,B种每个25元,在钱全部用完的情况下,有多少种购买方案( )A、2种 B、3种 C、4种 D、5种10. 如图是甲、乙两名射击运动员某节训练课的5次射击成绩的折线统计图,下列判断正确的是( )
A、 B、1 C、2 D、39. 学校计划用200元钱购买 、 两种奖品, 种每个15元,B种每个25元,在钱全部用完的情况下,有多少种购买方案( )A、2种 B、3种 C、4种 D、5种10. 如图是甲、乙两名射击运动员某节训练课的5次射击成绩的折线统计图,下列判断正确的是( )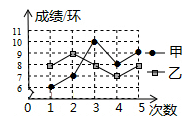 A、乙的最好成绩比甲高 B、乙的成绩的平均数比甲小 C、乙的成绩的中位数比甲小 D、乙的成绩比甲稳定11. 下列一元二次方程中,有两个不相等实数根的是( )A、 B、x2+2x+4=0 C、x2-x+2=0 D、x2-2x=012. 分式 化简后的结果为( )A、 B、 C、 D、13. 如图,在 中, 的平分线交 于点 交 的延长线于点 于点 ,若 ,则 的周长为( )
A、乙的最好成绩比甲高 B、乙的成绩的平均数比甲小 C、乙的成绩的中位数比甲小 D、乙的成绩比甲稳定11. 下列一元二次方程中,有两个不相等实数根的是( )A、 B、x2+2x+4=0 C、x2-x+2=0 D、x2-2x=012. 分式 化简后的结果为( )A、 B、 C、 D、13. 如图,在 中, 的平分线交 于点 交 的延长线于点 于点 ,若 ,则 的周长为( ) A、 B、 C、 D、14. 如图,在 中, ,以点O为圆心,2为半径的圆与 交于点C,过点C作 交 于点D,点P是边 上的动点.当 最小时, 的长为( )
A、 B、 C、 D、14. 如图,在 中, ,以点O为圆心,2为半径的圆与 交于点C,过点C作 交 于点D,点P是边 上的动点.当 最小时, 的长为( ) A、 B、 C、1 D、
A、 B、 C、1 D、二、填空题
-
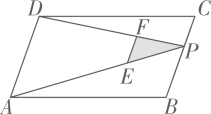
15. 因式分解:a-ab2=.16. 比 大且比 小的所有整数的和是 .17. 已知一次函数y=kx+b的图象经过A(1,﹣1),B(﹣1,3)两点,则k0(填“>”或“<”)18. 如图,P为平行四边形 边 上一点, 分别为 上的点,且 的面积分别记为 .若 则 .
 19. 将关于x的一元二次方程 变形为 ,就可以将 表示为关于x的一次多项式,从而达到“降次”的目的,又如 ,我们将这种方法称为“降次法”,通过这种方法可以化简次数较高的代数式.根据“降次法”,已知: ,且x>0,则 的值为 .
19. 将关于x的一元二次方程 变形为 ,就可以将 表示为关于x的一次多项式,从而达到“降次”的目的,又如 ,我们将这种方法称为“降次法”,通过这种方法可以化简次数较高的代数式.根据“降次法”,已知: ,且x>0,则 的值为 .三、解答题
-
20. 计算:21. 随着科技的进步和网络资源的丰富,在线阅读已成为很多人选择的阅读方式.为了解同学们在线阅读情况,某校园小记者随机调查了本校部分同学,并统计他们平均每天的在线阅读时间t(单位: ),然后利用所得数据绘制成如下不完整的统计图表.
在线阅读时间频数分布表
组别
在线阅读时间t
(人数)
A
4
B
8
C
a
D
16
E
2
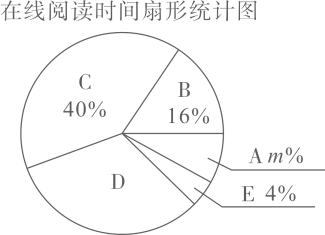
根据以上图表,解答下列问题:
(1)、这次被调查的同学共有人, , ;(2)、求扇形统计图中扇形D的圆心角的度数;(3)、若该校有950名学生,请估计全校有多少学生平均每天的在线阅读时间不少于 ?22. 图1是一种三角车位锁,其主体部分是由两条长度相等的钢条组成.当位于顶端的小挂锁打开时,钢条可放入底盒中(底盒固定在地面下),此时汽车可以进入车位;当车位锁上锁后,钢条按图1的方式立在地面上,以阻止底盘高度低于车位锁高度的汽车进入车位.图2是其示意图,经测量,钢条AB=AC=50cm,∠ABC=47°.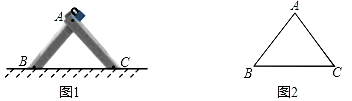 (1)、求车位锁的底盒长BC.(2)、若一辆汽车的底盘高度为30cm,当车位锁上锁时,问这辆汽车能否进入该车位?(参考数据:sin47°≈0.73,cos47°≈0.68,tan47°≈1.07)23. 经过实验获得两个变量x(x>0),y(y>0)的一组对应值如下表.
(1)、求车位锁的底盒长BC.(2)、若一辆汽车的底盘高度为30cm,当车位锁上锁时,问这辆汽车能否进入该车位?(参考数据:sin47°≈0.73,cos47°≈0.68,tan47°≈1.07)23. 经过实验获得两个变量x(x>0),y(y>0)的一组对应值如下表.x
1
2
3
4
5
6
y
6
2.9
2
1.5
1.2
1
 (1)、请画出相应函数的图象,并求出函数表达式.(2)、点A(x1 , y1),B(x2 , y2)在此函数图象上.若x1<x2 , 则y1 , y2有怎样的大小关系?请说明理由.24. 古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的是圆”.请研究如下美丽的圆.如图,线段AB是⊙O的直径,延长AB至点C,使BC=OB,点E是线段OB的中点,DE⊥AB交⊙O于点D,点P是⊙O上一动点(不与点A,B重合),连接CD,PE,PC.
(1)、请画出相应函数的图象,并求出函数表达式.(2)、点A(x1 , y1),B(x2 , y2)在此函数图象上.若x1<x2 , 则y1 , y2有怎样的大小关系?请说明理由.24. 古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的是圆”.请研究如下美丽的圆.如图,线段AB是⊙O的直径,延长AB至点C,使BC=OB,点E是线段OB的中点,DE⊥AB交⊙O于点D,点P是⊙O上一动点(不与点A,B重合),连接CD,PE,PC.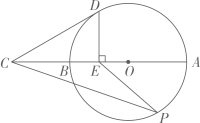 (1)、求证:CD是⊙O的切线;(2)、小明在研究的过程中发现 是一个确定的值.回答这个确定的值是多少?并对小明发现的结论加以证明.25. 在平面直角坐标系中,设二次函数y1=x2+bx+a , y2=ax2+bx+1(a , b是实数,a≠0).(1)、若函数y1的对称轴为直线x=3,且函数y1的图象经过点(a , b),求函数y1的表达式.(2)、若函数y1的图象经过点(r , 0),其中r≠0,求证:函数y2的图象经过点( ,0).(3)、设函数y1和函数y2的最小值分别为m和n , 若m+n=0,求m , n的值.26. 如图,正方形ABCD的边长为 ,M为AB的中点,△MBE为等边三角形,过点E作ME的垂线分别与边AD、BC相交于点F、G , 点P、Q分别在线段EF、BC上运动,且满足∠PMQ=60°,连接PQ .
(1)、求证:CD是⊙O的切线;(2)、小明在研究的过程中发现 是一个确定的值.回答这个确定的值是多少?并对小明发现的结论加以证明.25. 在平面直角坐标系中,设二次函数y1=x2+bx+a , y2=ax2+bx+1(a , b是实数,a≠0).(1)、若函数y1的对称轴为直线x=3,且函数y1的图象经过点(a , b),求函数y1的表达式.(2)、若函数y1的图象经过点(r , 0),其中r≠0,求证:函数y2的图象经过点( ,0).(3)、设函数y1和函数y2的最小值分别为m和n , 若m+n=0,求m , n的值.26. 如图,正方形ABCD的边长为 ,M为AB的中点,△MBE为等边三角形,过点E作ME的垂线分别与边AD、BC相交于点F、G , 点P、Q分别在线段EF、BC上运动,且满足∠PMQ=60°,连接PQ . (1)、求证:△MEP≌△MBQ .(2)、当点Q在线段GC上时,试判断PF+GQ的值是否变化?如果不变,求出这个值,如果变化,请说明理由.
(1)、求证:△MEP≌△MBQ .(2)、当点Q在线段GC上时,试判断PF+GQ的值是否变化?如果不变,求出这个值,如果变化,请说明理由.