高中数学苏教版（2019）5.1函数的概念和图象

试卷更新日期：2021-06-25 类型：同步测试

进入出卷网下载

一、填空题

1. 函数y＝－ax＋1与y＝ax²在同一坐标系中的图象大致是图中的.

查看试题解析
2. 函数y＝f(x)图象如图所示，

则：

(1)、f(0)＝；

(2)、f(－2)＝；

(3)、f[f（2）]＝；

(4)、若－1＜x₁≤x₂＜2，则f(x₁)与f(x₂)的大小关系为；

(5)、若f(x)＝0，则x＝.

查看试题解析
3. 下列对应或关系式中是A到B的函数的序号为.
① $A \in R ， B \in R$ ， $x^{2} + y^{2} = 1$ ；

②A＝{1，2，3，4}，B＝{0，1}，对应关系如图：

③ $A = R ， B = R$ ， $f ： x \to y = \frac{1}{x - 2}$ ；

④ $A = Z ， B = Z$ ， $f ： x \to y = \sqrt{2 x - 1}$ .

查看试题解析
4. 下列函数 $y = {(\sqrt{x})}^{2}$ ； $y = \frac{x^{2}}{x}$ ； $y = \sqrt[3]{x^{3}}$ ； $y = \sqrt{x^{2}}$ 与函数 $y = x$ 是同一函数的是.

查看试题解析
5. 设M＝{x|0≤x≤2}，N＝{y|0≤y≤2}，给出下列四个图形，其中能表示从集合M到集合N的函数关系的是.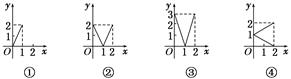

查看试题解析
6. 下列各组函数中，为同一函数的序号是.
⑴ $f (x) = x - 3$ 与 $g (x) = \sqrt{x^{2} - 6 x + 9}$ ；

⑵ $f (x) = | x - 1 |$ 与 $g (t) = \sqrt{t^{2} - 2 t + 1}$ ；

⑶ $f (x) = \frac{x^{2} - 4}{x + 2}$ 与 $g (x) = x - 2$ .

查看试题解析
7. 若f(x)＝ $\sqrt{\frac{1}{x}}$ 的定义域为M，g(x)＝ $\sqrt{x - 2}$ 的定义域为N，令全集为R，则 $∁_{R} (M \cap N)$ ＝.

查看试题解析
8. 若函数f(x)＝ax²－1，a为一个正数，且f(f(－1))＝－1，那么a的值是．

查看试题解析
9. 记函数f(x)＝ $\sqrt{3 - x}$ 的定义域为A，则A∩N中有个元素.

查看试题解析

二、解答题

10. 求下列函数的值域

(1)、 $y = x + 1$ ， $x \in {1 ， 2 ， 3 ， 4 ， 5}$ ；

(2)、 $y = \frac{x^{2} - 1}{x^{2} + 1}$ ；

(3)、 $y = - x^{2} - 2 x + 1$ ， $x \in [- 2 ， 1)$ ；

(4)、 $y = x + \sqrt{2 x + 1}$ .

查看试题解析
11. 画出函数f(x)＝－x²＋2x＋3的图象，并根据图象回答下列问题.

(1)、比较f(0)，f（1），f（3）的大小；

(2)、若x₁<x₂<1，比较f(x₁)与f(x₂)的大小；

(3)、求函数f(x)的值域；

(4)、若关于x的方程f(x)＝k在[－1，2]内仅有一个实根，求k的取值范围.

查看试题解析
12. 判断下列对应是否为函数：

(1)、x→y＝x，x∈{x|0≤x≤6}，y∈{y|0≤y≤3}；

(2)、x→y＝ $\frac{1}{6}$ x，x∈{x|0≤x≤6}，y∈{y|0≤y≤3}；

(3)、x→y＝3x＋1，x∈R，y∈R.

查看试题解析
13. 已知f(x)＝ $\frac{1 - x}{1 + x}$ (x≠－1).求：

(1)、f(0)及 $f (f (\frac{1}{2}))$ 的值；

(2)、f(1－x)及f(f(x)).

查看试题解析