云南省昆明市五华区2021年中考数学二模试卷

试卷更新日期：2021-06-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 数学就在我们身边，如神奇的天然建筑物——蜜蜂的巢房．它的截面呈正六边形，既节约空间又很坚固，巢房壁的厚度仅为 $0.000073$ 米．数字 $0.000073$ 用科学记数法表示为（）

A、 $73 \times 10^{- 6}$ B、 $0.73 \times 10^{- 4}$ C、 $7.3 \times 10^{- 4}$ D、 $7.3 \times 10^{- 5}$

查看试题解析
2. 如图所示的圆锥，下列说法正确的是（）

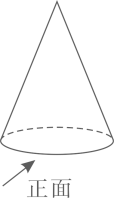A、该圆锥的主视图是轴对称图形 B、该圆锥的主视图是中心对称图形 C、该圆锥的主视图既是轴对称图形，又是中心对称图形 D、该圆锥的主视图既不是轴对称图形，又不是中心对称图形

查看试题解析
3. 某校学生会主席竞选中，参与投票的学生必须从进入决赛的四名选手中选 $1$ 名，且只能选 $1$ 名进行投票，根据投票结果，绘制了如下两幅不完整的统计图，则选手B的得票数为（）

A、 $80$ B、 $100$ C、 $120$ D、 $140$

查看试题解析
4. 如图，某停车场入口的栏杆从水平位置 $A B$ 绕点O旋转到 $A^{'} B^{'}$ 的位置．已知 $A O = 4$ 米，若栏杆的旋转角 $∠ A O A^{'} = 47 °$ ，则栏杆端点A上升的垂直距离 $A^{'} H$ 为（）

A、 $4 \sin 47 °$ 米 B、 $4 \cos 47 °$ 米 C、 $4 \tan 47 °$ 米 D、 $\frac{4}{\sin 47 °}$ 米

查看试题解析
5. 二十四节气，是我国古人根据地球在黄道（即地球绕太阳公转的轨道）上的位置变化而制定的，每一个节气分别相对应于地球在黄道上每运转15°所到达的一定位置，反映了太阳对地球产生的影响．它凝聚着中华文明的历史文化精华，在国际气象界，二十四节气被誉为“中国的第五大发明”．如图是地球绕太阳公转的轨道图，若将其近似看作圆形，其半径为Rkm，则从每年的立春到立夏，地球绕太阳公转的路程是（）

A、 $\frac{π R}{2}$ km B、 $\frac{π R}{3}$ km C、 $\frac{π R}{4}$ km D、 $\frac{5 π R}{12}$ km

查看试题解析
6. 一列数 $8^{1} ， 8^{2} ， 8^{3} ， 8^{4} ， \cdot \cdot \cdot ， 8^{2022}$ ，其中个位数字是8的数有（）

A、672个 B、506个 C、505个 D、252个

查看试题解析
7.
如图，矩形ABCD中，AB=3，BC=4，点P从A点出发，按A→B→C的方向在AB和BC上移动．记PA=x，点D到直线PA的距离为y，则y关于x的函数大致图象是（　　）

A、 B、 C、 D、

查看试题解析
8. 如图，方格纸中每个小正方形的边长均为1，其顶点称为格点． $△ A B C$ 的顶点都在小正方形的格点上．以点A为圆心，适当长为半径画弧，交 $A C$ 于点 M，交 $A B$ 于点N；分别以点M，N为圆心，大于 $\frac{1}{2} M N$ 的长为半径画弧，两弧在 $∠ C A B$ 的内部相交于点D；画射线 $A D$ 交 $B C$ 于点P，设 $C P = m$ ．点 Q为线段 $A B$ 上的动点，则下列结论：① $∠ A C B = 90^{\circ}$ ；②若分别连接 $D M$ ， $D N$ ，则 $D M = D N$ ；③当 $\frac{B P}{B C} = \frac{B Q}{B A}$ 时， $P Q ⊥ B C$ ；④ $P Q$ 的最小值为m．其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 在实数 $- 3$ ， $- \sqrt{7}$ ，2中，最小的数是．

查看试题解析
10. 如图， $∠ C B D = 90 °$ ， $A B / / E F$ ．若 $∠ A B C = 36 °$ ，则 $∠ D F E$ 是．

查看试题解析
11. 化简 $\frac{4 a^{2} - 4 b^{2}}{a^{2} - a b} =$ ．

查看试题解析
12. 函数 $y = \frac{\sqrt{x}}{4 x + 1}$ 的自变量x的取值范围是．

查看试题解析
13. 下图是某经营摄影器材公司的 $l o g o$ （公司的徽标）它由六个全等的直角三角形拼成，根据所学知识求出 $∠ A C B$ 是．

查看试题解析
14. 已知直线 $l ： y = - \frac{1}{2} x + 2$ ，若 $⊙ P$ 的半径为1，圆心P在y轴上，当 $⊙ P$ 与直线l相切时，则点P的坐标是．

查看试题解析

三、解答题

15. 计算： ${(- \frac{1}{2})}^{- 1} - \sqrt{18} + {(6 - \tan 72 °)}^{0} + | 1 - \sqrt{2} |$

查看试题解析
16. 如图所示， $A C ⊥ B C$ ， $D C ⊥ E C$ ，垂足均为点C，且 $A C = B C$ ， $E C = D C$ ．求证： $A E = B D$ ．

查看试题解析

17. 根据教育部关于学生使用手机的要求，某校开展了“放下手机，手捧书香”的活动，鼓励学生加强课外阅读，为了解学生课外阅读情况，抽样调查了部分学生每周用于课外阅读的时间：

（数据收集）从全校随机抽取20名学生，进行了每周用于课外阅读时间的调查，数据如下（单位： $\min$ ）

60，81，120，140，70，81，10，20，100，81

30，60，81，50，40，110，130，146，90，100

(1)、（数据整理）按下表分段分级整理样本数据并补全表格：

课外阅读时间 $x (\min)$	$0 \leq x < 40$	$40 \leq x < 80$	$80 \leq x < 120$	$120 \leq x < 160$
等级	A	B	C	D
人数	3	5	8

(2)、（数据分析）补全下列表格中的统计量：

平均数	中位数	众数
80

(3)、（结果运用）

估计该校全体学生每周用于课外阅读时间属于什么等级？请用样本中的统计量分析说明；

(4)、如果该校现有学生1500人，估计属于等级“B”的学生有多少名？

查看试题解析

18. 在目前疫情防控常态化背景下，某公司每周需要对面积为4800平方米的仓库进行一次全面消毒．最初采用人工消毒，为提高效率改用机器人完成任务．机器人每分钟消毒面积是人工的2倍，并且比人工提前40分钟完成任务．求机器人每分钟消毒面积为多少平方米？

查看试题解析
19. 甲、乙、丙、丁四个人玩“击鼓传花”的游戏，游戏规则是第一次由甲将花随机传给乙、丙、丁三人中的某一人，以后的每一次都是由接到花的人随机传给其他三人中的某一人

(1)、甲第一次传花时，恰好传给乙的概率是

(2)、请用画树状图或列表的方法求经过两次传花后，花恰好回到甲手中的概率

查看试题解析
20. 如图所示， $△ A B C ≌ △ E A D$ ，点 $E$ 在 $B C$ 上．

(1)、求证：四边形 $A B C D$ 是平行四边形；

(2)、若 $∠ B ∶ ∠ C A D = 3 ∶ 2$ ， $∠ E D C = 25 °$ ．求 $∠ A E D$ 的度数．

查看试题解析
21. 已知抛物线 $y = a x^{2} + 2 a x + 4 a^{2} - 5 (a \neq 0)$

(1)、该抛物线的对称轴为直线 $x =$ ；

(2)、若该抛物线的顶点在x轴上，求抛物线的解析式；

(3)、设点 $M (n ， y_{1})$ ， $N (1 ， y_{2})$ ，在该抛物线上，若 $y_{1} > y_{2}$ ，求n的取值范围．

查看试题解析
22. 五月我市周边的各种水果陆续成熟，吸引了广大市民前往观光采摘．果园经济带动了乡村采摘游，带动更多农户走向致富道路．郭家庄准备购买一批桑葚树和樱桃树共100棵，其中桑葚树不少于10棵，已知桑葚树的成活率为70%，樱桃树的成活率为90%，现在要求这批树的成活率不低于80%，桑葚树的单价 $y_{1}$ 和购买数量 $x_{1}$ 的函数关系以及樱桃树的单价 $y_{2}$ 和购买数量 $x_{2}$ 的函数关系分别如图1和图2所示．

(1)、写出 $y_{1}$ 关于 $x_{1}$ 的函数关系式

(2)、请你帮该农庄做个预算：购买这批树最少需要多少钱？

查看试题解析
23. 如图1，已知 $A C$ 、 $B D$ 为圆O的两条直径，连接 $A B$ ，过点O作 $O E ⊥ A B$ 于点E，取半径 $O C$ 的中点F，连接 $E F$ ，设 $∠ C A B = α$

(1)、如图2，若圆O的半径为3， $α = 30 °$ 时
①求证： $△ O E F$ 是等腰三角形．

②求图中阴影部分的面积

(2)、在（1）的条件下试确定经过A，B，F三点的圆的圆心位置和半径大小．

(3)、连接 $D F$ ，是否存在某个 $α$ 的值，使得 $D F$ 与 $E F$ 相等？若存在，求出此时 $\cos α$ 的值：若不存在，请说明理由．

查看试题解析