云南省昆明市盘龙区2021年中考数学二模试卷
试卷更新日期:2021-06-25 类型:中考模拟
一、单选题
-
1. 2020年一季度,受新冠肺炎疫情影响,云南省外贸进出口总值466.5亿元,较上年同期下降6.3%.2021年一季度,云南省外贸进出口总值达742.1亿元,同比增长59.7%.若下降6.3%,记作 ,则增长59.7%应记作( )A、 B、 C、 D、2. 下列标志中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,将木条a,b与c钉在一起, ,若要使木条a与b平行,则 的度数应为( )
3. 如图,将木条a,b与c钉在一起, ,若要使木条a与b平行,则 的度数应为( )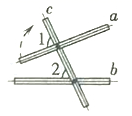 A、40° B、50° C、90° D、130°4. 下列运算正确的是( )A、 B、 C、 D、5. 下列说法正确的是( )A、“打开电视机,正在播放《云南新闻》”是必然事件 B、天气预报“明天降水的概率为50%”,是指明天有一半的时间会下雨 C、甲、乙两人在相同的条件下各射击10次,他们成绩的平均数相同,方差分别是 , ,则甲的成绩更稳定 D、为了了解一批灯泡的使用寿命,应采用全面调查的方式6. 定义运算: .例如 .则方程 的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、只有一个实数根7. 已知,如图,正方形 的面积为25,菱形 的面积为20,求阴影部分的面积( )
A、40° B、50° C、90° D、130°4. 下列运算正确的是( )A、 B、 C、 D、5. 下列说法正确的是( )A、“打开电视机,正在播放《云南新闻》”是必然事件 B、天气预报“明天降水的概率为50%”,是指明天有一半的时间会下雨 C、甲、乙两人在相同的条件下各射击10次,他们成绩的平均数相同,方差分别是 , ,则甲的成绩更稳定 D、为了了解一批灯泡的使用寿命,应采用全面调查的方式6. 定义运算: .例如 .则方程 的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、只有一个实数根7. 已知,如图,正方形 的面积为25,菱形 的面积为20,求阴影部分的面积( )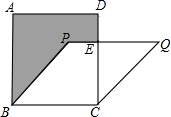 A、11 B、6.5 C、7 D、7.58. 如图,在平面直角坐标系中 条直线为 ,直线 交 轴于点 ,交 轴于点 ,直线 交 轴于点 ,过点 作 轴的平行线交 于点 ,点 关于 轴对称,抛物线 过 三点,下列判断中:① ;② ;③抛物线关于直线 对称;④抛物线过点 ;⑤四边形 ,其中正确的个数有( )
A、11 B、6.5 C、7 D、7.58. 如图,在平面直角坐标系中 条直线为 ,直线 交 轴于点 ,交 轴于点 ,直线 交 轴于点 ,过点 作 轴的平行线交 于点 ,点 关于 轴对称,抛物线 过 三点,下列判断中:① ;② ;③抛物线关于直线 对称;④抛物线过点 ;⑤四边形 ,其中正确的个数有( )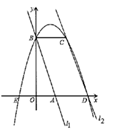 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
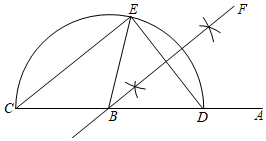
9. -3的绝对值等于。10. 极不平凡的2020年,云南统筹推进疫情防控和经济社会发展,在大战大考中交出优异答卷.2021年初,云南高速公路通车里程超过9000公里,跃居全国第二.数据9000用科学记数法表示为 .11. 如图,观察图中的尺规作图痕迹,若 , ,则 .
 12. 若实数a,b满足 ,则因式分解 .13. 如图,如果一只蚂蚁从圆锥底面上的点B出发,沿表面爬到母线AC的中点D处,则最短路线长为 .
12. 若实数a,b满足 ,则因式分解 .13. 如图,如果一只蚂蚁从圆锥底面上的点B出发,沿表面爬到母线AC的中点D处,则最短路线长为 .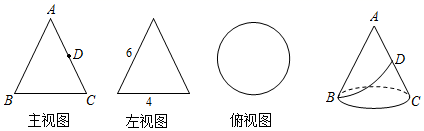 14. 如图,在矩形 中,点E是 的中点,点F为射线 上的一个动点, 沿着 折叠得到 ,连接 ,分别交 和 于点N和M,已知 , ,若 与 相似,则 的长是 .
14. 如图,在矩形 中,点E是 的中点,点F为射线 上的一个动点, 沿着 折叠得到 ,连接 ,分别交 和 于点N和M,已知 , ,若 与 相似,则 的长是 .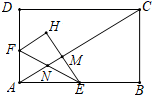
三、解答题
-
15. 计算: .16. 如图,已知 平分 , ,求证: .
 17. 2021年4月15日,是国家安全法颁布实施以来的第六个全民国家安全教育日.为了普及国家安全知识,提高维护国家安全意识,我市举办了国家安全保密知识竞赛.某校初一、初二、初三年级分别有学生300人,现从各年级中分别随机抽取20名学生的测试成绩(百分制,成绩均为整数),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息:
17. 2021年4月15日,是国家安全法颁布实施以来的第六个全民国家安全教育日.为了普及国家安全知识,提高维护国家安全意识,我市举办了国家安全保密知识竞赛.某校初一、初二、初三年级分别有学生300人,现从各年级中分别随机抽取20名学生的测试成绩(百分制,成绩均为整数),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息:(ⅰ)初一年级测试成绩的频数分布表如下(不完整):
初一年级测试成绩频数分布表
分组/分
频数
频率
2
0.1
2
0.1
0.2
12
合计
20
1.0
(ⅱ)初二年级测试成绩的频数分布直方图如下:
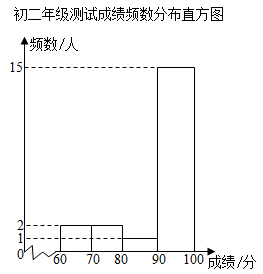
其中初二年级测试成绩在“ ”这一组的数据是:
95 100 96 99 98 98 99 97 99 100 100 99 100 95 100
(ⅲ)初三年级测试成绩的扇形统计图如下:
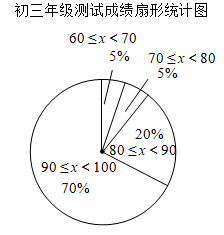
(ⅳ)初一、初二、初三年级测试成绩的平均数、众数、中位数和满分率如下(不完整):
年级
平均数
众数
中位数
满分率
初一
90
100
93
20%
初二
93
100
初三
92
99
96.5
10%
(说明:成绩90分及以上为优秀,80~89分为良好,60~79分为合格,60分以下为不合格)根据以上信息,回答下列问题:
(1)、在上述统计图表中 , , , ;(2)、初三年级测试成绩扇形统计图中“ ”部分所对的圆心角是度;(3)、根据以上数据分析:你认为哪个年级的竞赛成绩较好,并说明理由(至少从两个不同的角度说明推断的合理性)18. 观察以下等式:第1个等式:
第 个等式:
第3个等式:
第 个等式:
第5个等式:
······
按照以上规律.解决下列问题:
(1)、写出第6个等式;(2)、写出你猜想的第n个等式:(用含n的等式表示),并证明.19. 甲、乙两人玩摸牌游戏,把同一副扑克牌中的红桃1,2,3有数字的一面朝下放置,洗匀后甲先抽取一张,记下数字后将牌放回,洗匀后乙再抽取一张.设甲、乙两人抽到的牌面数字分别为x和y.(1)、请用列表法或树状图法(树状图也称树形图)中的一种方法,求 所有可能出现的结果;(2)、求甲、乙两人摸到的牌面数字组成的点 落在反比例函数 图象上的概率.20. 如图,已知点E是 中 边的中点,连接 并延长交 的延长线于点F,连接 , , .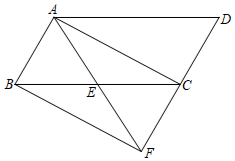 (1)、求证:四边形 为矩形;(2)、若 是等边三角形,且边长为4,求四边形 的面积.21. 某校喜迎中华人民共和国成立70周年,将举行以“歌唱祖国”为主题的歌咏比赛.需要在文具店购买国旗图案贴纸和小红旗发给学生做演出道具。已知每袋贴纸有50张.每袋小红旗有20面,贴纸和小红旗需整袋购买.每袋贴纸价格比每袋小红旗价格少5元.用150元购买贴纸所得袋数与用200元购买小红旗所得袋数相同.(1)、求每袋国旗图案贴纸和每袋小红旗的价格各是多少元?(2)、如果给每位演出学生分发国旗图案贴纸2张.小红旗1面.设购买国旗图案贴纸a袋(a为正整数).则购买小红旗多少袋能恰好配套?请用含a的代数式表示.(3)、在文具店累计购物超过800元后,超出800元的部分可享受8折优惠.学校按(2)中的配套方案购买,共支付w元.求w关于a的函数关系式.现全校有1200名学生参加演出,需要购买国旗图案贴纸和小红旗各多少袋?所需总费用多少元?22. 如图,以 为直径作 ,过点A作 的切线 ,连接 ,交 于点D,点E是 边的中点,连结 .
(1)、求证:四边形 为矩形;(2)、若 是等边三角形,且边长为4,求四边形 的面积.21. 某校喜迎中华人民共和国成立70周年,将举行以“歌唱祖国”为主题的歌咏比赛.需要在文具店购买国旗图案贴纸和小红旗发给学生做演出道具。已知每袋贴纸有50张.每袋小红旗有20面,贴纸和小红旗需整袋购买.每袋贴纸价格比每袋小红旗价格少5元.用150元购买贴纸所得袋数与用200元购买小红旗所得袋数相同.(1)、求每袋国旗图案贴纸和每袋小红旗的价格各是多少元?(2)、如果给每位演出学生分发国旗图案贴纸2张.小红旗1面.设购买国旗图案贴纸a袋(a为正整数).则购买小红旗多少袋能恰好配套?请用含a的代数式表示.(3)、在文具店累计购物超过800元后,超出800元的部分可享受8折优惠.学校按(2)中的配套方案购买,共支付w元.求w关于a的函数关系式.现全校有1200名学生参加演出,需要购买国旗图案贴纸和小红旗各多少袋?所需总费用多少元?22. 如图,以 为直径作 ,过点A作 的切线 ,连接 ,交 于点D,点E是 边的中点,连结 .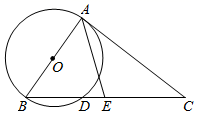 (1)、求证: ;(2)、若 , ,求 的长.23. 如图,在平面直角坐标系中,抛物线 经过点 ,点M为抛物线的顶点,点B在y轴上,且 ,直线 与抛物线在第一象限交于点 .
(1)、求证: ;(2)、若 , ,求 的长.23. 如图,在平面直角坐标系中,抛物线 经过点 ,点M为抛物线的顶点,点B在y轴上,且 ,直线 与抛物线在第一象限交于点 .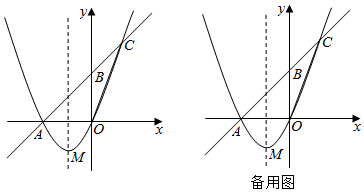 (1)、求抛物线的解析式及顶点M的坐标;(2)、求直线 的函数解析式及 的值;(3)、连接 ,若过点O的直线交线段 于点P,将 的面积分成1:2的两部分,请求出点P的坐标;(4)、在坐标平面内是否存在点N,使以点A、O、C、N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式及顶点M的坐标;(2)、求直线 的函数解析式及 的值;(3)、连接 ,若过点O的直线交线段 于点P,将 的面积分成1:2的两部分,请求出点P的坐标;(4)、在坐标平面内是否存在点N,使以点A、O、C、N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.