山东省邹城市2021年中考数学二模试卷
试卷更新日期:2021-06-25 类型:中考模拟
一、单选题
-
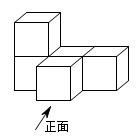
1. -9的绝对值是( )A、9 B、-9 C、 D、2. 当 时,下列分式没有意义的是( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 如图所示的几何体的俯视图是( )
 A、
A、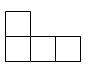 B、
B、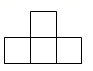 C、
C、 D、
D、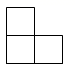 5. 不等式组 的解集在数轴上表示为( )A、
5. 不等式组 的解集在数轴上表示为( )A、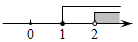 B、
B、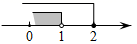 C、
C、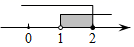 D、
D、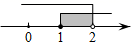 6. 如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若 ,则此斜坡的水平距离AC为( )
6. 如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若 ,则此斜坡的水平距离AC为( ) A、75m B、50m C、30m D、12m7. 如图,菱形ABCD的对角线AC、BD相交于点O , 过点D作DH⊥AB于点H , 连接OH , 若OA=6,S菱形ABCD=48,则OH的长为( )
A、75m B、50m C、30m D、12m7. 如图,菱形ABCD的对角线AC、BD相交于点O , 过点D作DH⊥AB于点H , 连接OH , 若OA=6,S菱形ABCD=48,则OH的长为( )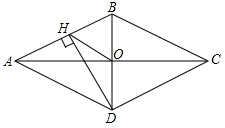 A、4 B、8 C、 D、68. 如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为( )
A、4 B、8 C、 D、68. 如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为( )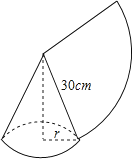 A、5cm B、10cm C、20cm D、5πcm9. 如图,二次函数y=ax2+bx+c(a≠0)图象的对称轴为直线x=﹣1,下列结论:①abc<0;②3a<﹣c;③若m为任意实数,则有a﹣bm≤am2+b; ④若图象经过点(﹣3,﹣2),方程ax2+bx+c+2=0的两根为x1 , x2(|x1|<|x2|),则2x1﹣x2=5.其中正确的结论的个数是( )
A、5cm B、10cm C、20cm D、5πcm9. 如图,二次函数y=ax2+bx+c(a≠0)图象的对称轴为直线x=﹣1,下列结论:①abc<0;②3a<﹣c;③若m为任意实数,则有a﹣bm≤am2+b; ④若图象经过点(﹣3,﹣2),方程ax2+bx+c+2=0的两根为x1 , x2(|x1|<|x2|),则2x1﹣x2=5.其中正确的结论的个数是( ) A、4个 B、3个 C、2个 D、1个10. 如图,四边形 是边长为1的正方形,点 是射线 上的动点(点 不与点 ,点 重合),点 在线段 的延长线上,且 ,连接 ,将 绕点 顺时针旋转90°得到 ,连接 .设 ,四边形 的面积为 ,下列图象能正确反映出 与 的函数关系的是( )
A、4个 B、3个 C、2个 D、1个10. 如图,四边形 是边长为1的正方形,点 是射线 上的动点(点 不与点 ,点 重合),点 在线段 的延长线上,且 ,连接 ,将 绕点 顺时针旋转90°得到 ,连接 .设 ,四边形 的面积为 ,下列图象能正确反映出 与 的函数关系的是( )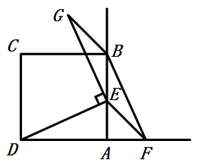 A、
A、 B、
B、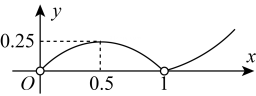 C、
C、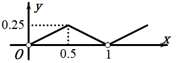 D、
D、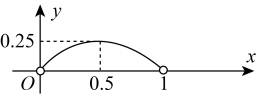
二、填空题
-
11. 分解因式: .12. 分式方程 =1的解为 .
13. 如图,在矩形 中,按以下步骤作图:①分别以点A和C为圆心,以大于 的长为半径作弧,两弧相交于点M和N;②作直线 交 于点E.若 , ,则矩形的对角线 的长为 .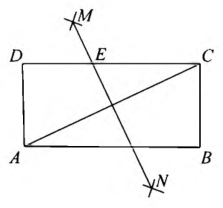 14. 如图,一艘船以40nmile/h的速度由西向东航行,航行到A处时,测得灯塔P在船的北偏东30°方向上,继续航行2.5h,到达B处,测得灯塔P在船的北偏西60°方向上,此时船到灯塔的距离为nmile.(结果保留根号)
14. 如图,一艘船以40nmile/h的速度由西向东航行,航行到A处时,测得灯塔P在船的北偏东30°方向上,继续航行2.5h,到达B处,测得灯塔P在船的北偏西60°方向上,此时船到灯塔的距离为nmile.(结果保留根号) 15. 如图,在矩形 中,E是 上的一点,连接 ,将△ 进行翻折,恰好使点A落在 的中点F处,在 上取一点O,以点O为圆心, 的长为半径作半圆与 相切于点G;若 ,则图中阴影部分的面积为 .
15. 如图,在矩形 中,E是 上的一点,连接 ,将△ 进行翻折,恰好使点A落在 的中点F处,在 上取一点O,以点O为圆心, 的长为半径作半圆与 相切于点G;若 ,则图中阴影部分的面积为 .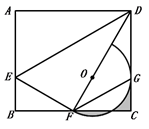
三、解答题
-
16. 计算: .17. 中华文化源远流长,文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如下尚不完整的统计图.
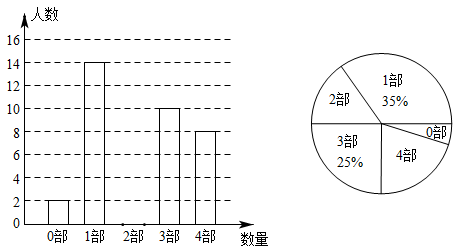
请根据以上信息,解决下列问题:
(1)、本次调查所得数据的众数是部,中位数是部;(2)、扇形统计图中“4部”所在扇形的圆心角为度;(3)、请将条形统计图补充完整;(4)、没有读过四大古典名著的两名学生准备从中各自随机选择一部来阅读,请用列表或画树状图的方法求他们恰好选中同一名著的概率.18. 已知一次函数 与反比例函数 的图象交于 、 两点.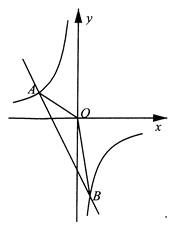 (1)、求一次函数和反比例函数的表达式;(2)、求 的面积;(3)、点P在x轴上,当 为等腰三角形时,直接写出点P的坐标.19. 如图, 是⊙O的直径,C是⊙O上一点,D是 的中点,E为 延长线上一点,且 与 交于点H , 与 交于点F .
(1)、求一次函数和反比例函数的表达式;(2)、求 的面积;(3)、点P在x轴上,当 为等腰三角形时,直接写出点P的坐标.19. 如图, 是⊙O的直径,C是⊙O上一点,D是 的中点,E为 延长线上一点,且 与 交于点H , 与 交于点F .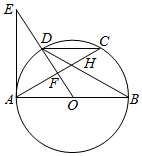 (1)、求证: 是⊙O的切线;(2)、若直径 的长为 ,求 的长.20. 某水果店一次购进了若干箱蜜桔和苹果,已知购进蜜橘花费800元,购进苹果花费1680元,所购苹果比蜜桔多10箱,苹果每箱的进价是蜜桔每箱进价的1.4倍.(1)、蜜橘和苹果每箱进价分别为多少元?(2)、根据市场情况,每箱苹果可以比每箱蜜桔的利润多5元,这批水果全部售完后,店家若想获得不少于800元的利润,应该如何确定每箱蜜桔和草果的售价?21. 综合与实践
(1)、求证: 是⊙O的切线;(2)、若直径 的长为 ,求 的长.20. 某水果店一次购进了若干箱蜜桔和苹果,已知购进蜜橘花费800元,购进苹果花费1680元,所购苹果比蜜桔多10箱,苹果每箱的进价是蜜桔每箱进价的1.4倍.(1)、蜜橘和苹果每箱进价分别为多少元?(2)、根据市场情况,每箱苹果可以比每箱蜜桔的利润多5元,这批水果全部售完后,店家若想获得不少于800元的利润,应该如何确定每箱蜜桔和草果的售价?21. 综合与实践在线上教学中,教师和学生都学习到了新知识,掌握了许多新技能.例如教材八年级下册的数学活动﹣﹣折纸,就引起了许多同学的兴趣.在经历图形变换的过程中,进一步发展了同学们的空间观念,积累了数学活动经验.
实践发现:
对折矩形纸片ABCD , 使AD与BC重合,得到折痕EF , 把纸片展平;再一次折叠纸片,使点A落在EF上的点N处,并使折痕经过点B , 得到折痕BM , 把纸片展平,连接AN , 如图①.
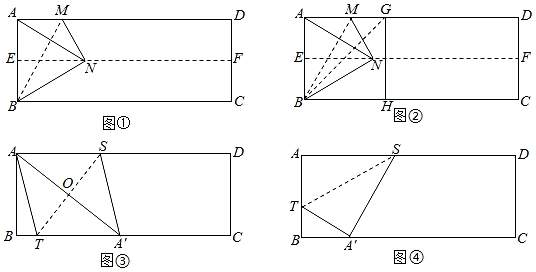 (1)、折痕BM(填“是”或“不是”)线段AN的垂直平分线;请判断图中△ABN是什么特殊三角形?答:;进一步计算出∠MNE=°;(2)、继续折叠纸片,使点A落在BC边上的点H处,并使折痕经过点B , 得到折痕BG , 把纸片展平,如图②,则∠GBN=°;(3)、拓展延伸:
(1)、折痕BM(填“是”或“不是”)线段AN的垂直平分线;请判断图中△ABN是什么特殊三角形?答:;进一步计算出∠MNE=°;(2)、继续折叠纸片,使点A落在BC边上的点H处,并使折痕经过点B , 得到折痕BG , 把纸片展平,如图②,则∠GBN=°;(3)、拓展延伸:如图③,折叠矩形纸片ABCD , 使点A落在BC边上的点A'处,并且折痕交BC边于点T , 交AD边于点S , 把纸片展平,连接AA'交ST于点O , 连接AT .
求证:四边形SATA'是菱形.
(4)、如图④,矩形纸片ABCD中,AB=10,AD=26,折叠纸片,使点A落在BC边上的点A'处,并且折痕交AB边于点T , 交AD边于点S , 把纸片展平.同学们小组讨论后,得出线段AT的长度有4,5,7,9.请写出以上4个数值中你认为正确的数值 .22. 如图,在平面直角坐标系中, ,且 ,点A的坐标是 .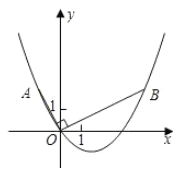 (1)、求点B的坐标;(2)、求过点 的抛物线的表达式;(3)、连接AB,在(2)中的抛物线上求出点P,使得
(1)、求点B的坐标;(2)、求过点 的抛物线的表达式;(3)、连接AB,在(2)中的抛物线上求出点P,使得