山东省淄博市周村区（五四制）2021年中考数学一模试卷

试卷更新日期：2021-06-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列选项中的数，与无理数 $\sqrt{10}$ 最接近的是（）

A、1 B、2 C、3 D、4

查看试题解析
2. 清代·袁枚的一首诗《苔》中的诗句：“白日不到处，青春恰自来.苔花如米小，也学牡丹开.”若苔花的花粉直径约为0.0000084米，则数据0.0000084用科学记数法表示为（）

A、8.4×10^-5 B、8.4×10^-6 C、84×10^-7 D、8.4×10⁶

查看试题解析
3. 下列运算正确的是（）

A、（﹣x﹣1）（x﹣1）＝1﹣x² B、（x﹣2）²＝x²﹣4 C、（﹣2a²）³＝﹣8a⁸ D、（a＋2b）²＝a²＋4ab＋2b²

查看试题解析
4. 点 $A (4 ， 3)$ 经过某种图形变化后得到点 $B (- 3 ， 4)$ ，这种图形变化可以是（）

A、关于 $x$ 轴对称 B、关于 $y$ 轴对称 C、绕原点逆时针旋转 $90^{\circ}$ D、绕原点顺时针旋转 $90^{\circ}$

查看试题解析
5. 用反证法证明：“直角三角形至少有一个锐角不小于45°”时，应先假设（）

A、直角三角形的每个锐角都小于45° B、直角三角形有一个锐角大于45° C、直角三角形的每个锐角都大于45° D、直角三角形有一个锐角小于45°

查看试题解析
6. 在如图所示的正方形网格中，点A，B，C，D，O均在格点上，则点O是（）

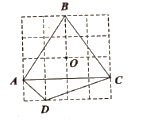A、 $△ A C D$ 的外心 B、 $△ A C D$ 的内心 C、 $△ A B C$ 的外心 D、 $△ A B C$ 的内心

查看试题解析
7. 已知一次函数 $y_{1} = 2 x - 2$ ，二次函数 $y_{2} = x^{2}$ ，对于x的同一个值，这两个函数所对应的函数值分别为 $y_{1}$ 和 $y_{2}$ ，则下列表述正确的是（）

A、 $y_{1} > y_{2}$ B、 $y_{1} < y_{2}$ C、 $y_{1} = y_{2}$ D、 $y_{1}$ ， $y_{2}$ 的大小关系不确定

查看试题解析
8. 如图是一圆锥的左视图，根据图中所示数据，可得圆锥侧面展开图的圆心角的度数为（）

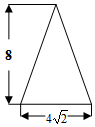A、60° B、90° C、120° D、135°

查看试题解析
9. 如图，四边形 $A B C D$ 中，E，F，G，H依次是各边中点，O是四边形 $A B C D$ 内的一点.若四边形 $A E O H$ ， $B F O E$ ， $C G O F$ 的面积分别为5，6，7，则四边形 $D H O G$ 的面积为（）

A、5.5 B、6 C、6.5 D、7

查看试题解析
10. 如图，在等边三角形 $A B C$ 中， $B C = 6$ ，点D是边 $A B$ 上一点，且 $B D = 2$ ，点P是边 $B C$ 上一动点（D，P两点均不与端点重合），作 $∠ D P E = 60 °$ ， $P E$ 交边 $A C$ 于点E．若 $C E = a$ ，当满足条件的点P有且只有一个时，则a的值为（）

A、4 B、5 C、 $\frac{13}{3}$ D、 $\frac{9}{2}$

查看试题解析
11. 甲、乙两地之间是一条直路，在全民健身活动中，赵明阳跑步从甲地往乙地，王浩月骑自行车从乙地往甲地，两人同时出发，王浩月先到达目的地，两人之间的距离 $s (km)$ 与运动时间 $t (h)$ 的函数关系大致如图所示，下列说法中错误的是（）．

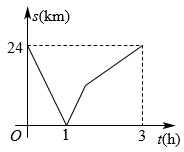A、两人出发1小时后相遇 B、赵明阳跑步的速度为 $8 km / h$ C、王浩月到达目的地时两人相距 $10 km$ D、王浩月比赵明阳提前 $1.5 h$ 到目的地

查看试题解析
12. 如图，点E是正方形 $A B C D$ 内一点，点E到点A，B和D的距离分别为1， $2 \sqrt{2}$ ， $\sqrt{10}$ ，延长 $A E$ 与 $B C$ 相交于点F，则 $E F$ 的长为（）

A、3 B、4 C、 $\frac{8}{3}$ D、 $\frac{10}{3}$

查看试题解析

二、填空题

13. 计算： $5^{2} + {(- 1)}^{0}$ 的结果是．

查看试题解析
14. 一个不透明盒子里有3张形状大小质地完全相同的卡片，上面分别标有数字1，2，3．从中随机抽出一张后不放回，再从盒中随机抽出一张，则两次抽出的卡片都是奇数的概率为．

查看试题解析
15. 若双曲线 $y = \frac{k - 1}{x}$ 向右平移2个单位后经过点（4，1），则k的值是．

查看试题解析
16. 如图， $A B$ ， $C D$ 是圆O的两条相等的弦，弧 $A D$ ，弧 $B C$ 的度数分别为30度，120度，P为劣弧 $A B$ 上一点，则 $∠ A P B =$ °．

查看试题解析

17. 为了更好地开展全民健身，建设健康中国，某社区随机抽取了若干居民，对其健身情况进行抽样调查．将被调查的居民每天的健身时间

t (min)

分为5组，绘制如下的不完整的健身时间频数分布表和扇形统计图．

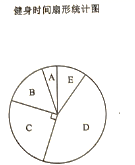
健身时间频数分布表
健身时间 $t (min)$	频数	频率
A组： $25 \leq t < 35$	m	█
B组： $35 \leq t < 45$	█	0.15
C组： $45 \leq t < 55$	150	█
D组： $55 \leq t < 65$	270	█
E组： $65 \leq t < 75$	█	0.10
合计	a	1

根据上述信息，解答下列问题：

(1)、在扇形统计图中，C组对应的圆心角为直角，频数分布表中a的值是；

(2)、在频数分布表中，m的值为，在扇形统计图中，A组的圆心角为；

(3)、在本次统计中，中位数落在组；

(4)、若该社区共有3万人，利用本次抽样调查的结果，可估计该社区锻炼时间不少于45分钟的人数为万人．

查看试题解析

18. 如图，在矩形 $A B C D$ 中， $B C = 4$ ，E为 $C D$ 上一点，将 $△ B C E$ 沿 $B E$ 折叠，使点C正好落在 $A D$ 边上的F处，作 $∠ A B F$ 的平分线交 $A D$ 于N，交 $E F$ 的延长线于M，若 $N F = 2$ ，则 $A B$ 的长为．

查看试题解析

三、解答题

19. 解不等式组 ${\begin{array}{l} 2 x \leq x + 1 ， ① \\ 4 x + 1 \geq 2 x - 5 ． ② \end{array}$ 请按下列步骤完成解答：
（I）解不等式①，得      ▲      ；

（Ⅱ）解不等式②，得      ▲      ；

（Ⅲ）把不等式①和②的解集在数轴上表示出来；

（IV）原不等式组的解集为      ▲      ．

查看试题解析
20. 如图，在平行四边形 $A B C D$ 中， $A C$ ， $B D$ 相交于点O，点E，F在 $B D$ 上，且 $B E = D F$ ．连接 $A E$ ， $C F$ ．

(1)、求证： $△ A O E ≌ △ C O F$ ；

(2)、若 $A C ⊥ E F$ ，连接 $A F$ ， $C E$ ，判断四边形 $A E C F$ 的形状，并说明理由．

查看试题解析
21. 如图，一个梯子 $A B$ 斜靠在一面墙上，梯子底端为A，梯子的顶端B距地面的垂直距离为 $B C$ 的长．

(1)、若梯子的长度是 $10 m$ ，梯子的顶端B距地面的垂直距离为 $8 m$ ．如果梯子的顶端下滑 $1 m$ ，那么梯子的底端A向外滑动多少米?

(2)、设 $A B = c$ ， $B C = a$ ， $A C = b$ ，且 $a > b$ ，请思考，梯子在滑动的过程中，是否一定存在顶端下滑的距离与底端向外滑动的距离相等的情况?若存在，请求出这个距离；若不存在，说明理由．

查看试题解析
22. 如图，线段 $A B$ 是圆O的直径，延长 $A B$ 至点C，使 $B C = O B$ ，点E是线段 $O B$ 的中点， $D E ⊥ A B$ 交圆O于点D，点P是圆O上的一动点（不与点A，B重合），连接 $C D$ ， $P E$ ， $P C$ ．

(1)、求证： $C D$ 是圆O的切线；

(2)、求 $\frac{P E}{P C}$ 的值．

查看试题解析
23. 如图，P为正方形 $A B C D$ 对角线 $A C$ 上的一点，连接 $D P$ 并延长交 $A B$ 于点E，过P作 $M N ⊥ D E$ 分别交 $B C$ ， $A D$ 于M，N．

(1)、如图1，求证： $M N = D E$ ；

(2)、如图2，点F与点C关于直线 $D E$ 对称，连接 $F A$ 并延长交直线 $D E$ 于点G，连接 $B G$ ．
①设 $∠ A D E$ 的度数为x，求 $∠ D G F$ 的度数：

②猜想 $A F$ 与 $B G$ 之间的数量关系，并证明．

查看试题解析
24. 如图，在平面直角坐标系 $x O y$ 中，抛物线 $y = a x^{2} - 2 x + c$ 与x轴交于点A和点 $B (1 ， 0)$ ，与y轴相交于点 $C (0 ， 3)$ ．

(1)、求抛物线的解析式和顶点D的坐标；

(2)、找出图中与 $∠ D A B$ 相等的一个角，并证明；

(3)、若点P是第二象限内抛物线上的一点，当点P到直线 $A C$ 的距离最大时，求点P的坐标．

查看试题解析