山东省淄博市博山区2021年中考数学一模试卷
试卷更新日期:2021-06-25 类型:中考模拟
一、单选题
-
1. 的绝对值是( )A、–2 B、2 C、 D、2. 如图图形中,既是轴对称图形又是中心对称图形的是( )A、
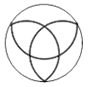 B、
B、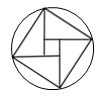 C、
C、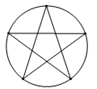 D、
D、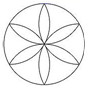 3. 不等式组 的解集为( )A、 B、 C、 D、4. 如图,在下列条件中,不能证明△ABD≌△ACD的条件是( )
3. 不等式组 的解集为( )A、 B、 C、 D、4. 如图,在下列条件中,不能证明△ABD≌△ACD的条件是( )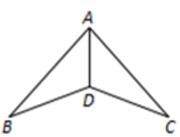 A、BD=DC,AB=AC B、∠ADB=∠ADC,BD=DC C、∠B=∠C,∠BAD=∠CAD D、∠B=∠C,BD=DC5. 若用我们数学课本上采用的科学计算器进行计算,其按键顺序如图,则输出结果应为( )
A、BD=DC,AB=AC B、∠ADB=∠ADC,BD=DC C、∠B=∠C,∠BAD=∠CAD D、∠B=∠C,BD=DC5. 若用我们数学课本上采用的科学计算器进行计算,其按键顺序如图,则输出结果应为( ) A、2 B、 C、 D、6. 根据如图所示的程序计算函数y的值,若输入的x的值为3或-4时,输出的y值互为相反数,则b等于( )
A、2 B、 C、 D、6. 根据如图所示的程序计算函数y的值,若输入的x的值为3或-4时,输出的y值互为相反数,则b等于( ) A、-30 B、-23 C、23 D、307. 如图,一次函数 的图象与反比例函数 的图象的一个交点为 ,则不等式 的解集是( )
A、-30 B、-23 C、23 D、307. 如图,一次函数 的图象与反比例函数 的图象的一个交点为 ,则不等式 的解集是( ) A、 B、 C、 D、 或8. 便民商店经营一种商品,在销售过程中,发现一周利润y(元)与每件销售价x(元)之间的关系满足y=-2(x-20)2+1558,由于某种原因,价格只能15≤x≤22,那么一周可获得最大利润是( )A、20 B、1508 C、1550 D、15589. 如图,在矩形ABCD中,把∠A沿DF折叠,点A恰好落在矩形的对称中心E处,则∠ADF的度数为( )
A、 B、 C、 D、 或8. 便民商店经营一种商品,在销售过程中,发现一周利润y(元)与每件销售价x(元)之间的关系满足y=-2(x-20)2+1558,由于某种原因,价格只能15≤x≤22,那么一周可获得最大利润是( )A、20 B、1508 C、1550 D、15589. 如图,在矩形ABCD中,把∠A沿DF折叠,点A恰好落在矩形的对称中心E处,则∠ADF的度数为( ) A、15° B、20° C、25° D、30°10. 设a,b是方程 的两个实数根,则 的值为( )A、2020 B、2021 C、2022 D、202311. 如图, 中, , , ,点G是AB上的一个动点,过点G作GF垂直于AC于点F , 点P是BC上的点.若 是以GF为斜边的等腰直角三角形.则此时PC长为( ).
A、15° B、20° C、25° D、30°10. 设a,b是方程 的两个实数根,则 的值为( )A、2020 B、2021 C、2022 D、202311. 如图, 中, , , ,点G是AB上的一个动点,过点G作GF垂直于AC于点F , 点P是BC上的点.若 是以GF为斜边的等腰直角三角形.则此时PC长为( ).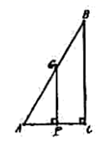 A、 B、 C、 D、12. 如图,半径为1的⊙O与直线l相切于点A,C为⊙O上的一点, 于点B,则 的最大值是( )
A、 B、 C、 D、12. 如图,半径为1的⊙O与直线l相切于点A,C为⊙O上的一点, 于点B,则 的最大值是( ) A、2 B、 C、 D、
A、2 B、 C、 D、二、填空题
-
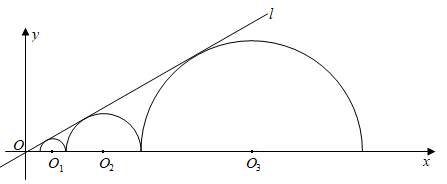
13. tan60°的值等于 .14. 用a,b,c表示二次函数 (其中a,b,c为常数且 )的顶点坐标为( , ).15. 若方程 有两个解 和 ,则 的值为 .16. 如果一组数据5、8、a、7、4的平均数是a,那么这组数据的方差为17. 如图,圆心都在 轴正半轴上的半圆 ,半圆 ,……半圆 与直线l相切.设半圆 ,半圆 ,……,半圆 的半径分别是 , ,……, ,则当直线l与x轴所成锐角为 ,且 时, .
三、解答题
-
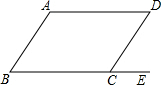
18. 解方程:19. 已知在四边形ABCD中,AD=BC,∠D=∠DCE.求证:四边形ABCD是平行四边形.
 20. 自新冠肺炎疫情爆发以来,我国人民上下一心,团结一致,基本控制住了疫情.然而,全球新冠肺炎疫情依然严重,境外许多国家的疫情尚在继续蔓延,疫情防控不可松懈. 如图是某国截止5月31日新冠病毒感染人数的扇形统计图和折线统计图.
20. 自新冠肺炎疫情爆发以来,我国人民上下一心,团结一致,基本控制住了疫情.然而,全球新冠肺炎疫情依然严重,境外许多国家的疫情尚在继续蔓延,疫情防控不可松懈. 如图是某国截止5月31日新冠病毒感染人数的扇形统计图和折线统计图.
根据上面图表信息,回答下列问题:
(1)、截止5月31日该国新冠肺炎感染总人数累计为 万人,扇形统计图中40-59岁感染人数对应圆心角的度数为° ;(2)、请直接在图中补充完整该国新冠肺炎感染人数的折线统计图;(3)、在该国所有新冠肺炎感染病例中随机地抽取1人,求该患者年龄为60岁或60岁以上的概率;(4)、若该国感染病例中从低到高各年龄段的死亡率依次为 、 、 、 、 ,求该国新冠肺炎感染病例的平均死亡率.21. 随着我国首艘自主建造航母“山东舰”的正式服役,标志者我国已进入“双航母”时代.已知“山东舰”舰长 为 ,航母前端点E到水平甲板 的距离 为 ,舰岛顶端A到 的距离是 ,经测量, , .(参考数据: , , , , , ) (1)、若设 ,用含x的代数式表示 与 的长度.(2)、请计算舰岛 的高度(结果精确到 ).22. 如图,已知反比例函数 的图象经过点 ,过A作 轴于点C.点B为反比例函数图象上的一动点,过点B作 轴于点D,连接 .直线 与x轴的负半轴交于点E.
(1)、若设 ,用含x的代数式表示 与 的长度.(2)、请计算舰岛 的高度(结果精确到 ).22. 如图,已知反比例函数 的图象经过点 ,过A作 轴于点C.点B为反比例函数图象上的一动点,过点B作 轴于点D,连接 .直线 与x轴的负半轴交于点E. (1)、求k的值;(2)、连接 ,求 的面积;(3)、若 ,求四边形 的面积.23. 已知:AB,CD都是⊙O的直径,点E为 上一点,连接BE,CE,且∠BEC=45°.
(1)、求k的值;(2)、连接 ,求 的面积;(3)、若 ,求四边形 的面积.23. 已知:AB,CD都是⊙O的直径,点E为 上一点,连接BE,CE,且∠BEC=45°.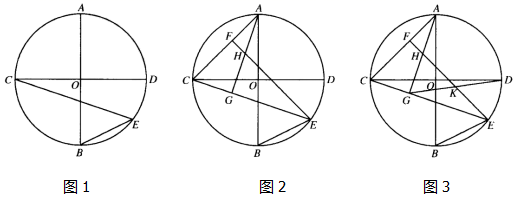 (1)、如图1,求证:AB⊥CD;(2)、如图2,连接AC,过点E作EF⊥AC,垂足为点F,过点A作AG⊥CE,垂足为点G,交EF于点H,求证:AC=EH;(3)、如图3,在(2)的条件下,连接DG,若∠DGE=∠CAG,BE=2 ,求EH的长.24. 如图,抛物线 交轴于点 , ,交y轴于点C, ,点E是线段 上一动点,作 交线段 于点F.
(1)、如图1,求证:AB⊥CD;(2)、如图2,连接AC,过点E作EF⊥AC,垂足为点F,过点A作AG⊥CE,垂足为点G,交EF于点H,求证:AC=EH;(3)、如图3,在(2)的条件下,连接DG,若∠DGE=∠CAG,BE=2 ,求EH的长.24. 如图,抛物线 交轴于点 , ,交y轴于点C, ,点E是线段 上一动点,作 交线段 于点F.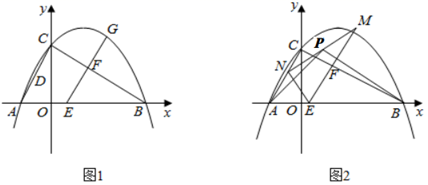 (1)、求抛物线的解析式;(2)、如图1,延长线段 交抛物线于点G,点D是 边中点,当四边形 为平行四边形时,求出G点坐标;(3)、如图2,M为射线 上一点,且 ,将射线 绕点E逆时针旋转 ,交直线 于点N,连接 ,P为 的中点,连接 , ,问: 是否存在最小值,若存在,请求出这个最小值,若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、如图1,延长线段 交抛物线于点G,点D是 边中点,当四边形 为平行四边形时,求出G点坐标;(3)、如图2,M为射线 上一点,且 ,将射线 绕点E逆时针旋转 ,交直线 于点N,连接 ,P为 的中点,连接 , ,问: 是否存在最小值,若存在,请求出这个最小值,若不存在,请说明理由.