人教版2019必修一 第四章 指数函数与对数函数单元练习
试卷更新日期:2021-06-25 类型:单元试卷
一、单选题
-
1. 以下运算正确的是( )A、 B、 C、 D、2. 已知 , , ,则( )A、 B、 C、 D、3. 函数 的零点在区间( ).A、
 B、
B、 C、
C、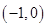 D、
D、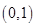 4. 已知函数 ,若函数 有两个不同的零点,则 的取值范围( )A、 B、
4. 已知函数 ,若函数 有两个不同的零点,则 的取值范围( )A、 B、 C、
C、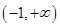 D、
D、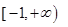 5. 已知 ,若关于 的方程 有三个实根,则实数 的取值范围是( )A、
5. 已知 ,若关于 的方程 有三个实根,则实数 的取值范围是( )A、 B、
B、 C、
C、 D、
D、 6. 当 且 时,函数 必过定点A、
6. 当 且 时,函数 必过定点A、 B、
B、 C、
C、 D、
D、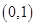 7. 若xlog23=1,则3x+9x的值为( )A、3 B、6 C、2 D、8. 已知函数 的图象如图所示,则函数 与 在同一直角坐标系中的图象是
7. 若xlog23=1,则3x+9x的值为( )A、3 B、6 C、2 D、8. 已知函数 的图象如图所示,则函数 与 在同一直角坐标系中的图象是 A、
A、 B、
B、 C、
C、 D、
D、 9. 若a>1,b>0,ab+a-b=2 ,则ab-a-b等于( )A、 B、2或-2 C、-2 D、210. 已知1是函数f(x)=ax2+bx+c(a>b>c)的一个零点,若存在实数x0 . 使得f(x0)<0.则f(x)的另一个零点可能是( )A、
9. 若a>1,b>0,ab+a-b=2 ,则ab-a-b等于( )A、 B、2或-2 C、-2 D、210. 已知1是函数f(x)=ax2+bx+c(a>b>c)的一个零点,若存在实数x0 . 使得f(x0)<0.则f(x)的另一个零点可能是( )A、 B、
B、 C、
C、 D、
D、 11. 设函数 ,则满足 的x的取值范围是A、
11. 设函数 ,则满足 的x的取值范围是A、 B、
B、 C、
C、 D、
D、 12. 给出定义:若 (其中 为整数),则 叫做离实数 最近的整数,记作 ,即 .设函数 ,二次函数 ,若函数 与 的图象有且只有一个公共点,则 的取值不可能是( )A、
12. 给出定义:若 (其中 为整数),则 叫做离实数 最近的整数,记作 ,即 .设函数 ,二次函数 ,若函数 与 的图象有且只有一个公共点,则 的取值不可能是( )A、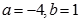 B、
B、 C、
C、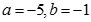 D、
D、
二、填空题
-
13. 计算: =.14. 计算: .15. 已知函数f(x)= ,则f(x)的单调递增区间是 .16. 定义在R上的奇函数 ,当 时,则 ,则关于x的函数 的所有零点之和为 .
三、解答题
-
17. 不用计算器求下列各式的值(1)、 ;(2)、 .18. 已知函数f(x)=ax-1(x≥0).其中a>0,a≠1.(1)、若f(x)的图象经过点( ,2),求a的值;(2)、求函数y=f(x)(x≥0)的值域.19. 设 ,且 .(1)、求 的值及 的定义域;(2)、求 在区间 上的值域.20. 已知函数 有两个零点.(1)、若函数的两个零点是 和 ,求 的值;(2)、若函数的两个零点是 和 ,求 的取值范围.21. 某地区预计从明年初开始的前几个月内,对某种商品的需求总量f(x)(万件)与月份数x的近似关系为f(x)= x(x+1)(35﹣2x)(x∈N,x≤12).(1)、写出明年第x个月的需求量g(x)(万件)与月份数x的函数关系;(2)、求出需求量最大的月份数x,并求出这前x个月的需求总量.22. 已知函数f(x)=log2(x+1),当点(x,y)是函数y=f(x)图象上的点时,点( , )是函数y=g(x)图象上的点.(1)、写出函数y=g(x)的表达式;(2)、当g(x)﹣f(x)≥0时,求x的取值范围.(3)、若方程f(x)﹣g(x)﹣m=0有两个不同的实数根,求实数m的取值范围.