山东省青岛市即墨区2021年中考数学一模试卷

试卷更新日期：2021-06-25 类型：中考模拟

进入出卷网下载

一、单选题

1. $- \sqrt{5}$ 的绝对值是（）

A、 $\sqrt{5}$ B、 $- \sqrt{5}$ C、 $- \frac{1}{\sqrt{5}}$ D、5

查看试题解析
2. 下列标志图中，既是轴对称图形，又是中心对称图形的是（）．

A、 B、 C、 D、

查看试题解析
3. 习近平同志在十九大报告中指出：农业农村农民问题是关系到国计民生的根本性问题，我国现有农村人口约为589 730 000人，将589 730 000用科学记数法表示为（）

A、589 73×10⁴ B、589.73×10⁶ C、5.8973×10⁸ D、0.58973×10⁸

查看试题解析
4. 下列运算正确的是（）

A、 $2 x^{2} y + 3 x y = 5 x^{3} y^{2}$ B、 ${(- 2 a b^{2})}^{3} = - 6 a^{3} b^{6}$ C、 ${(3 a + b)}^{2} = 9 a^{2} + b^{2}$ D、 $(3 a + b) (3 a - b) = 9 a^{2} - b^{2}$

查看试题解析
5. 如图，PA、PB是⊙O切线，A、B为切点，点C在⊙O上，且∠ACB＝55°，则∠APB等于（）

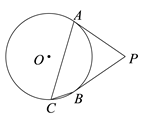A、55° B、70° C、110° D、125°

查看试题解析
6. 如图，将 $△ A B C$ 先向上平移1个单位，再绕点P按逆时针方向旋转 $90 °$ ，得到 $△ A^{'} B^{'} C'$ ，则点A的对应点 $A'$ 的坐标是（）

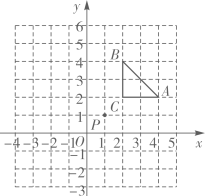A、（0，4） B、（2，-2） C、（3，-2） D、（-1，4）

查看试题解析
7. 如图，矩形ABCD中，AB=12，点E是AD上的一点，AE=6，BE的垂直平分线交BC的延长线于点F ，连接EF交CD于点G ，若G是CD的中点，则BC的长是（）

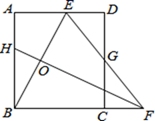A、12.5 B、12 C、10 D、10.5

查看试题解析
8. 在同一坐标系中，二次函数 $y = a x^{2} + b x$ 与一次函数 $y = b x - a$ 的图像可能是（）

A、 B、 C、 D、

查看试题解析

二、填空题

9. 计算： $\frac{3}{\sqrt{3}} + {(\sqrt{3} - 3)}^{0} - 2^{- 1} - \cos 60 °$ = ．

查看试题解析
10. 一组数据6，4，x ， 3，2的平均数是5，则这组数据的方差为．

查看试题解析
11. 如图，C为半圆内一点，O为圆心，直径AB长为4cm ， ∠BOC=60°，∠BCO=90°，将△BOC绕圆心O逆时针旋转至△B′OC′ ，点C′在OA上，则边BC扫过区域（图中阴影部分）的面积为cm² ．

查看试题解析
12. 如图，在平面直角坐标系中，点A（-3，1），以点O为顶点作等腰直角三角形AOB ，双曲线 $y_{1} = \frac{k_{1}}{x}$ 在第一象限内的图象经过点B ．设直线AB的表达式为 $y_{2} = k_{2} x + b$ ，当y₁＞y₂时，x的取值范围是．

查看试题解析
13. 如图，在矩形ABCD中，AB=4，点E，F分别在BC，CD上，将△ABE沿AE折叠，使点B落在AC上的点B′处，又将△CEF沿EF折叠，使点C落在直线EB′与AD的交点C′处，DF= ．

查看试题解析
14. 如图，若△ABC内一点P满足∠PAC＝∠PCB＝∠PBA，则称点P为△ABC的布罗卡尔点，已知△ABC中，CA＝CB，∠ACB＝120°，P为△ABC的布罗卡尔点，若 $PA = \sqrt{3}$ ，则PB+PC＝．

查看试题解析

三、解答题

15. 如图，有一块三角形材料(△ABC)，请你在这块材料上作一个面积最大的圆．

查看试题解析
16.

(1)、化简： $1 - (\frac{1}{a + 3} + \frac{6}{a^{2} - 9}) \div \frac{a + 3}{a^{2} - 6 a + 9}$

(2)、解不等式组： ${\begin{array}{l} 2 (x + 1) > x \\ 1 - 2 x \geq \frac{x + 7}{2} \end{array}$

查看试题解析
17. 某中学为了了解本校学生的上学方式，在全校范围内随机抽查了部分学生，将收集的数据绘制成两幅不完整的统计图如图所示，请根据图中提供的信息，解答下列问题：

(1)、这次共抽取名学生进行调查；并补全条形图；

(2)、扇形统计图中“步行”所在扇形的圆心角为．

(3)、如果该校共有1500名学生，请你估计该校骑自行车上学的学生有多少名？

查看试题解析
18. 袋子中装有2个红球，1个黄球，它们除颜色外其余都相同．小丽和小红做摸球游戏，约定游戏规则是：小丽先从袋中任意摸出1个球记下颜色后放回，小红再从袋中摸出1个球记下颜色后放回，如果两人摸到的球的颜色相同，小丽赢，否则小红赢．这个游戏规则对双方公平吗？请说明理由．

查看试题解析
19. 某幼儿园准备改善原有滑梯的安全性能，把倾斜角由原来的40°减为35°，已知原滑梯AB的长为5米，为了改造后新滑梯的安全，滑梯前方必须有2米的空地，请问距离原来滑梯B处3米的大树对滑梯的改造有影响吗？（sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，Sin35°≈0.57，cos35°≈0.82，tan35°≈0.70）

查看试题解析
20. 为了加快“智慧校园”建设，某市准备为试点学校采购一批 $A$ 、 $B$ 两种型号的一体机，经过市场调查发现，今年每套 $B$ 型一体机的价格比每套 $A$ 型一体机的价格多0.6万元，且用960万元恰好能购买500套 $A$ 型一体机和200套 $B$ 型一体机.

(1)、求今年每套 $A$ 型、 $B$ 型一体机的价格各是多少万元

(2)、该市明年计划采购 $A$ 型、 $B$ 型一体机1100套，考虑物价因素，预计明年每套 $A$ 型一体机的价格比今年上涨25%，每套 $B$ 型一体机的价格不变，若购买 $B$ 型一体机的总费用不低于购买 $A$ 型一体机的总费用，那么该市明年至少需要投入多少万元才能完成采购计划？

查看试题解析
21. 已知：在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点．过点A作AF∥BC交BE的延长线于点F

(1)、求证：△AEF≌△DEB；

(2)、当△ABC满足什么条件时，四边形ADCF是正方形？请说明理由．

查看试题解析
22. 即墨古城某城门横断面分为两部分，上半部分为抛物线形状，下半部分为正方形（OMNE为正方形），已知城门宽度为4米，最高处离地面6米，如图1所示，现以O点为原点，OM所在的直线为x轴，OE所在的直线为y轴建立直角坐标系．

(1)、求出上半部分抛物线的函数表达式，并写出其自变量的取值范围；

(2)、有一辆宽3米，高4.5米的消防车需要通过该城门进入古城，请问该消防车能否正常进入？

(3)、为营造节日气氛，需要临时搭建一个矩形“装饰门”ABCD ，该“装饰门”关于抛物线对称轴对称，如图2所示，其中AB ， AD ， CD为三根承重钢支架，A、D在抛物线上，B ， C在地面上，已知钢支架每米50元，问搭建这样一个矩形“装饰门”，仅钢支架一项，最多需要花费多少元？

查看试题解析
23. 小明学完了“锐角三角函数”的相关知识后，通过研究发现：如图1，在Rt△ABC中，如果∠C=90°，∠A=30°，BC=a=1，AC=b= $\sqrt{3}$ ，AB=c=2，那么 $\frac{a}{\sin A} = \frac{b}{\sin B} = 2$ ．通过上网查阅资料，他又知“sin90°=1”，因此他得到“在含30°角的直角三角形中，存在着 $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$ 的关系”．

这个关系对于一般三角形还适用吗？为此他做了如下的探究：

(1)、如图2，在Rt△ABC中，∠C=90°，BC=a ， AC=b ， AB=c ，请判断此时“ $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$ ”的关系是否成立？答：．

(2)、完成上述探究后，他又想“对于任意的锐角△ABC ，上述关系还成立吗？”因此他又继续进行了如下的探究：
如图3，在锐角△ABC中，BC=a ， AC=b ， AB=c ，过点C作CD⊥AB于D ，设CD=h ，

∵在Rt△ADC和Rt△BDC中，∠ADC=∠BDC=90°，

∴sinA= ， sinB= ．

∴ $\frac{a}{\sin A}$ = ， $\frac{b}{\sin B}$ = ．

∴ $\frac{a}{\sin A} = \frac{b}{\sin B}$

同理，过点A作AH⊥BC于H ，可证 $\frac{b}{\sin B} = \frac{c}{\sin C}$

∴ $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

请将上面的过程补充完整．

(3)、运用上面结论解答下列问题：
①如图4，在△ABC中，如果∠A=75°，∠B=60°，AB=6，求AC的长．

②在△ABC中，如果∠B=30°，AB= $2 \sqrt{3}$ ，AC=2，那么△ABC内切圆的半径为．

查看试题解析
24. 已知，如图，在△ABC中，AB=AC=10cm，BC=12cm，AD⊥BC于点D ，直线PM交BC于点P ，交AC于点M，直线PM从点C出发沿CB方向匀速运动，速度为1cm/s；运动过程中始终保持PM⊥BC ，过点P作PQ⊥AB ，交AB于点Q ，交AD于点N ，连接QM ，设运动时间是t(s)(0＜t＜6)，解答下列问题：

(1)、当t为何值时，QM//BC？

(2)、设四边形ANPM的面积为y(cm²)，试求出y与t的函数关系式；

(3)、是否存在某一时刻t ，使四边形ANPM的面积是△ABC面积的 $\frac{1}{3}$ ？若存在，求出t的值；若不存在，请说明理由；

(4)、是否存在某一时刻t ，使点M在线段PQ的垂直平分线上？若存在，求出t的值；若不存在，请说明理由．

查看试题解析