山东省青岛莱西市(五四制)2021年中考数学一模试卷
试卷更新日期:2021-06-25 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、2021 B、 C、 D、2. 下列图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 天王星围绕太阳公转的轨道半径长约为 ,数字2 900 000 000用科学记数法表示为( )A、 B、 C、 D、4. 如图,在平面直角坐标系中,△ABC的顶点都在格点上,如果将△ABC先沿y轴翻折,再向上平移3个单位长度,得到 ',那么点B的对应点B'的坐标为( )
3. 天王星围绕太阳公转的轨道半径长约为 ,数字2 900 000 000用科学记数法表示为( )A、 B、 C、 D、4. 如图,在平面直角坐标系中,△ABC的顶点都在格点上,如果将△ABC先沿y轴翻折,再向上平移3个单位长度,得到 ',那么点B的对应点B'的坐标为( )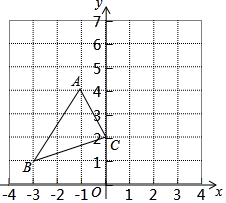 A、(1,7) B、(0,5) C、(3,4) D、(﹣3,2)5. 某个几何体的三视图如图所示,该几何体是( )
A、(1,7) B、(0,5) C、(3,4) D、(﹣3,2)5. 某个几何体的三视图如图所示,该几何体是( ) A、
A、 B、
B、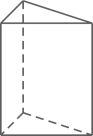 C、
C、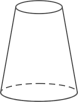 D、
D、 6. 如图,AB为⊙O的切线,点A为切点,OB交⊙O于点C , 点D在⊙O上,连接AD、CD , OA , 若∠ABO =20°,则∠ADC的度数为( )
6. 如图,AB为⊙O的切线,点A为切点,OB交⊙O于点C , 点D在⊙O上,连接AD、CD , OA , 若∠ABO =20°,则∠ADC的度数为( ) A、20° B、30° C、35° D、40°7. 如图,正方形ABCD边长为4,点E、F分别是BC、CD上的点,且CE=CF=1,点P、Q分别是AF、EF的中点,连接PD、PQ、DQ , 则线段DQ的长等于( )
A、20° B、30° C、35° D、40°7. 如图,正方形ABCD边长为4,点E、F分别是BC、CD上的点,且CE=CF=1,点P、Q分别是AF、EF的中点,连接PD、PQ、DQ , 则线段DQ的长等于( ) A、4 B、 C、 D、8. 如图,正比例函数 ,一次函数y2=2x+b和反比例函数 的图象在同一直角坐标系中,若y1>y3>y2 , 则自变量x的取值范围是( )
A、4 B、 C、 D、8. 如图,正比例函数 ,一次函数y2=2x+b和反比例函数 的图象在同一直角坐标系中,若y1>y3>y2 , 则自变量x的取值范围是( ) A、x<-1 B、-2<x< C、 <x<0 D、-2<x<-1
A、x<-1 B、-2<x< C、 <x<0 D、-2<x<-1二、填空题
-
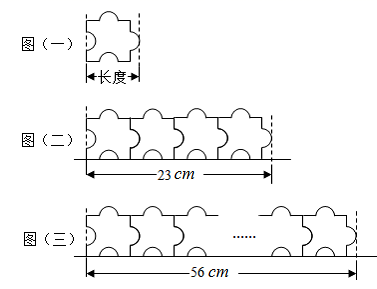
9. 计算: = .10. 已知有若干片相同的拼图,其形状如图(一)所示.当4片拼图紧密拼成一列时长度为23cm,如图(二)所示.当10片拼图紧密拼成一列时长度为56cm,如图(三)所示.则图(一)中的拼图长度为cm.
 11. 为了解某校学生的睡眠情况,该校数学小组随机调查了部分学生一周的平均每天睡眠时间,设每名学生的平均每天睡眠时间为x时,共分为四组:A.6≤x<7,B.7≤x<8,C.8≤x<9,D.9≤x≤10,将调查结果绘制成如图两幅不完整的统计图:注:学生的平均每天睡眠时间不低于6时且不高于10时.
11. 为了解某校学生的睡眠情况,该校数学小组随机调查了部分学生一周的平均每天睡眠时间,设每名学生的平均每天睡眠时间为x时,共分为四组:A.6≤x<7,B.7≤x<8,C.8≤x<9,D.9≤x≤10,将调查结果绘制成如图两幅不完整的统计图:注:学生的平均每天睡眠时间不低于6时且不高于10时.
若该校有1500名学生,根据抽样调查结果,请估计该校平均每天睡眠时间低于8时的学生有人.
12. 若函数 的图象与x轴没有交点,则m的取值范围是 .13. 如图,将矩形ABCD绕着点A逆时针旋转得到矩形AEFG , 点B的对应点E落在边CD上,若AB= ,BC= ,则 长为 . 14. 如图是一个棱长为2cm的正方体,用一平面经过CC1中点E截这个正方体,截面△BED的面积为 .
14. 如图是一个棱长为2cm的正方体,用一平面经过CC1中点E截这个正方体,截面△BED的面积为 . 15. 某射击队教练为了了解队员的训练情况,从队员中选取甲、乙两名队员进行射击测试,相同条件下各射击5次,成绩统计如表:
15. 某射击队教练为了了解队员的训练情况,从队员中选取甲、乙两名队员进行射击测试,相同条件下各射击5次,成绩统计如表:命中环数
6
7
8
9
10
甲命中相应环数的次数
0
1
3
1
0
乙命中相应环数的次数
2
0
0
2
1
(1)、根据上述信息可知:甲命中环数的中位数是环,乙命中环数的众数是环;(2)、试通过计算说明甲、乙两人的成绩谁比较稳定.三、解答题
-
16. 已知:△ABC .
求作:⊙O , 使它同时与AB、AC相切,且O点在BC上.
(用圆规、直尺作图,不写作法,但要保留作图痕迹.)
 17.(1)、计算: ;(2)、解不等式组: .18. 小李和小王两位同学做游戏,在一个不透明的口袋中放入1个红球、2个白球、1个黑球,这些球除颜色外都相同,将球摇匀.(1)、从中任意摸出1个球,恰好摸到红球的概率是多少?(2)、两人约定:从袋中一次摸出两个球,若摸出的两个球是-红一黑,则小李获胜:若摸出的两个球都是白色,则小王获胜,请用列举法(画树状图或列表)分析游戏规则是否公平.19. 某次台风来袭时,一棵笔直且垂直于地面的大树AB被刮倾斜后在C处折断倒在地上,树的顶部恰好接触到地面D处,测得∠ACD=60°,∠ADC=37°,AD=5米,求这棵大树AB的高.(结果精确到0.1米)(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75, ≈1.73)
17.(1)、计算: ;(2)、解不等式组: .18. 小李和小王两位同学做游戏,在一个不透明的口袋中放入1个红球、2个白球、1个黑球,这些球除颜色外都相同,将球摇匀.(1)、从中任意摸出1个球,恰好摸到红球的概率是多少?(2)、两人约定:从袋中一次摸出两个球,若摸出的两个球是-红一黑,则小李获胜:若摸出的两个球都是白色,则小王获胜,请用列举法(画树状图或列表)分析游戏规则是否公平.19. 某次台风来袭时,一棵笔直且垂直于地面的大树AB被刮倾斜后在C处折断倒在地上,树的顶部恰好接触到地面D处,测得∠ACD=60°,∠ADC=37°,AD=5米,求这棵大树AB的高.(结果精确到0.1米)(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75, ≈1.73) 20. 防疫期间某工厂接生产N95口罩和普通医用外科口罩共180万个的生产任务.该工厂不能同时生产两种口罩,且生产普通医用外科口罩的速度是生产N95口罩速度的2倍,生产40万只N95口罩比生产40万只普通医用外科口罩多用4天.(1)、求该工厂每天能生产N95口罩或生产普通医用外科口罩多少只?(2)、若每生产一只N95口罩可获利0.6元,每生产一只普通医用外科口罩可获利0.25元,且生产工期不能超过26天,则如何安排生产工厂获利最多?最多获利多少万元?21. 如图,平行四边形ABCD , BE⊥AD于E , 交AC于M , DF⊥BC于F , 交AC于N , 连结DM、BN .
20. 防疫期间某工厂接生产N95口罩和普通医用外科口罩共180万个的生产任务.该工厂不能同时生产两种口罩,且生产普通医用外科口罩的速度是生产N95口罩速度的2倍,生产40万只N95口罩比生产40万只普通医用外科口罩多用4天.(1)、求该工厂每天能生产N95口罩或生产普通医用外科口罩多少只?(2)、若每生产一只N95口罩可获利0.6元,每生产一只普通医用外科口罩可获利0.25元,且生产工期不能超过26天,则如何安排生产工厂获利最多?最多获利多少万元?21. 如图,平行四边形ABCD , BE⊥AD于E , 交AC于M , DF⊥BC于F , 交AC于N , 连结DM、BN . (1)、求证:△ABM≌△CDN;(2)、当▱ABCD是菱形时,判断四边形MBND的形状,并说明理由.22. 如图,一小球M从斜坡OA上的O点处抛出,球的抛出路线是抛物线的一部分,建立如图所示的平面直角坐标系,斜坡可以用一次函数 刻画.若小球到达的最高的点坐标为(4,8),解答下列问题:
(1)、求证:△ABM≌△CDN;(2)、当▱ABCD是菱形时,判断四边形MBND的形状,并说明理由.22. 如图,一小球M从斜坡OA上的O点处抛出,球的抛出路线是抛物线的一部分,建立如图所示的平面直角坐标系,斜坡可以用一次函数 刻画.若小球到达的最高的点坐标为(4,8),解答下列问题: (1)、求抛物线的表达式;(2)、小球落点为A , 求A点的坐标;(3)、在斜坡OA上的B点有一棵树,B点的横坐标为2,树高为4,小球M能否飞过这棵树?通过计算说明理由;(4)、求小球M在飞行的过程中离斜坡OA的最大高度.23. 由特殊到一般、类比探究都是数学学习过程中重要的思想和方法,请你结合所学知识完成下列问题.
(1)、求抛物线的表达式;(2)、小球落点为A , 求A点的坐标;(3)、在斜坡OA上的B点有一棵树,B点的横坐标为2,树高为4,小球M能否飞过这棵树?通过计算说明理由;(4)、求小球M在飞行的过程中离斜坡OA的最大高度.23. 由特殊到一般、类比探究都是数学学习过程中重要的思想和方法,请你结合所学知识完成下列问题.

(特殊思考)
如图1,正方形ABCD中,AE=AF , 连接EF , 易知BE与DF的数量关系为:BE=DF;BE与DF的位置关系为:BE⊥DF .
(1)、(一般问题)将图1中的三角形AEF绕点A旋转,在旋转过程中,BE与DF的数量关系和位置关系是否发生改变?结合图2,说明理由.
(2)、(类比探究)若将(1)中的正方形变为矩形,等腰Rt△AEF变为Rt△AEF , 且AD=2AB , AF=2AE , 其他条件不变.(1)中的结论是否发生变化?结合图3,说明理由.
24. 已知如图,△ABC中,AB=AC=5cm,BC=8cm.点P从点A出发,沿AC方向匀速运动,速度为1cm/s;同时,点Q从点C出发,沿CB方向匀速运动,速度为2cm/s,当Q停止平移时,点P也停止运动.过P做PE BC , 交AB于E , 连结EQ . 设运动时间为t(s)(0<t<4).解答下列问题: (1)、当t为何值时,PQ=QC?(2)、设△PQC的面积为y(cm2),求y与t之间的函数关系式;(3)、是否存在某一时刻t , 使S△PQC∶S四边形AEQP=3∶4?若存在,求出t的值;若不存在,请说明理由;(4)、是否存在某一时刻t , 使PQ⊥EQ?若存在,求出t的值;若不存在,请说明理由.
(1)、当t为何值时,PQ=QC?(2)、设△PQC的面积为y(cm2),求y与t之间的函数关系式;(3)、是否存在某一时刻t , 使S△PQC∶S四边形AEQP=3∶4?若存在,求出t的值;若不存在,请说明理由;(4)、是否存在某一时刻t , 使PQ⊥EQ?若存在,求出t的值;若不存在,请说明理由.