山东省临沂市罗庄区2021年中考数学二模试卷
试卷更新日期:2021-06-25 类型:中考模拟
一、单选题
-
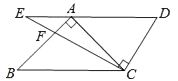
1. 若 ,那么a、b、c三数的大小为( ).A、 B、 C、 D、2. 花粉的质量很小,一粒某种植物花粉的质量约为0.000037毫克,已知1克=1000毫克,那么0.000037毫克可用科学记数法表示为( )A、3.7×10﹣5克 B、3.7×10﹣6克 C、37×10﹣7克 D、3.7×10﹣8克3. 将一副三角板如图放置,使点A在DE上,BC∥DE,则∠ACE的度数为( )
 A、10° B、15° C、20° D、25°4. 圆锥的主视图与左视图都是边长为4的等边三角形,则圆锥的侧面展开图扇形的圆心角是( )
A、10° B、15° C、20° D、25°4. 圆锥的主视图与左视图都是边长为4的等边三角形,则圆锥的侧面展开图扇形的圆心角是( )
A、90° B、120° C、150° D、180°5. 已知x=3是关于x的方程 的解,则 的值是( )A、2 B、-2 C、1 D、﹣16. 等式 成立的条件是( )A、x≠2 B、x≥﹣2 C、x≥﹣2且x≠2 D、x>27. 若(a2+b2﹣3)2=25,则a2+b2=( )A、8或﹣2 B、﹣2 C、8 D、2或﹣88. 在运动会上,小亮、小莹、小刚和小勇四位同学代表九年级(3)班参加4×100米接力比赛,小勇跑最后一棒,其他三人抽签排定序号,小亮和小刚进行接棒的概率是A、 B、 C、 D、9. 在“建设美丽阜新”的行动中,需要铺设一段全长为 的污水排放管道.为了尽量减少施工时对城市交通所造成的影响,实际施工时每天的工效比原计划增加25%,结果提前30天完成这一任务.设实际每天铺 管道,根据题意,所列方程正确的是( )A、 B、 C、 D、10. 已知一组数据x1 , x2 , x3....xn的方差是2,则另一组数据3x1+2,3x2+2,3x3+2,...3xn+2,方差是( )A、6 B、8 C、18 D、2011. 化简(a﹣1)÷( ﹣1)•a的结果是( )A、﹣a2 B、1 C、a2 D、﹣112. 如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD , 已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4 , 以下判断,其中错误的是( )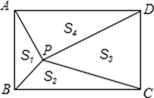 A、PA+PB+PC+PD的最小值为10 B、若△PAB≌△PCD , 则△PAD≌△PBC C、若△PAB∼△PDA , 则PA=2 D、若S1=S2 , 则S3=S413. 如图,在直角坐标系xOy中,点P的坐标为(4,3),PQ⊥x轴于Q , M , N分别为OQ , OP上的动点,则QN+MN的最小值为( )
A、PA+PB+PC+PD的最小值为10 B、若△PAB≌△PCD , 则△PAD≌△PBC C、若△PAB∼△PDA , 则PA=2 D、若S1=S2 , 则S3=S413. 如图,在直角坐标系xOy中,点P的坐标为(4,3),PQ⊥x轴于Q , M , N分别为OQ , OP上的动点,则QN+MN的最小值为( )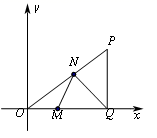 A、 B、 C、 D、14. 如图,正方形ABCD的边长为5,动点P的运动路线为A→B→C , 动点Q的运动路线为B→D.点P与Q以相同的均匀速度分别从A , B两点同时出发,当一个点到达终点停止运动时另一个点也随之停止.设点P运动的路程为x , △BPQ的面积为y , 则下列能大致表示y与x的函数关系的图象为( )
A、 B、 C、 D、14. 如图,正方形ABCD的边长为5,动点P的运动路线为A→B→C , 动点Q的运动路线为B→D.点P与Q以相同的均匀速度分别从A , B两点同时出发,当一个点到达终点停止运动时另一个点也随之停止.设点P运动的路程为x , △BPQ的面积为y , 则下列能大致表示y与x的函数关系的图象为( )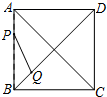 A、
A、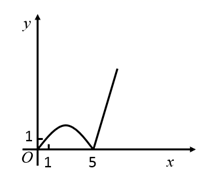 B、
B、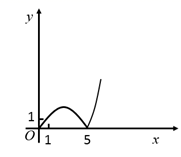 C、
C、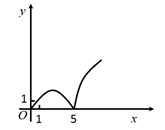 D、
D、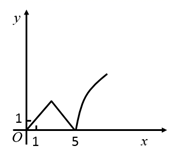
二、填空题
-
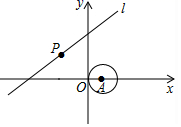
15. 不等式 的解集是.16. 若关于x的一元二次方程 有两个相等的实数根,则 的值为 .17. 如图,在直角坐标系中,⊙A的圆心A的坐标为(1,0),半径为1,点P为直线y= x+3上的动点,过点P作⊙A的切线,切点为Q , 则切线长PQ的最小值是 .
 18. 如图,D、E分别是△ABC的边AB、AC上的点,且D E∥BC , BE、CD相交于点O , 若S△DOE:S△DOB=1:3,则当S△ADE=2时,四边形DBCE的面积是 .
18. 如图,D、E分别是△ABC的边AB、AC上的点,且D E∥BC , BE、CD相交于点O , 若S△DOE:S△DOB=1:3,则当S△ADE=2时,四边形DBCE的面积是 .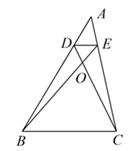 19. 定义运算:若am=b , 则logab=m(a>0),例如23=8,则log28=3.运用以上定义,计算:log5125﹣log381=
19. 定义运算:若am=b , 则logab=m(a>0),例如23=8,则log28=3.运用以上定义,计算:log5125﹣log381=三、解答题
-
20. 计算:﹣32+4cos30°﹣|1﹣ |+(π﹣2021)0+21. 促进青少年健康成长是实施“健康中国”战略的重要内容.为了引导学生积极参与体育运动,某校举办了一分钟跳绳比赛,随机抽取了40名学生一分钟跳绳的次数进行调查统计,并根据调查统计结果绘制了如表格和统计图:

等级
次数
频率
不合格
100≤x 120
a
合格
120≤x 140
b
良好
140≤x 160
优秀
160≤x 180
请结合上述信息完成下列问题:
(1)、a= , b=;(2)、请补全频数分布直方图;(3)、在扇形统计图中,“良好”等级对应的圆心角的度数是;(4)、若该校有2000名学生,根据抽样调查结果,请估计该校学生一分钟跳绳次数达到合格及以上的人数.22. 如图,在南北方向的海岸线MN上,有A , B两艘巡逻船,现均收到故障船C的求救信号,已知A , B两船相距100( +1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D , 测得船C正好在观测点D的南偏东75°方向上.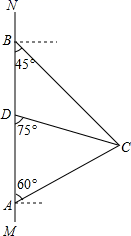 (1)、求出A与C之间的距离AC .(2)、已知距观测点D处100海里范围内有暗礁.若巡逻船A沿直线AC去营救船C , 在去营救的途中有无触暗礁危险?(参考数据: ≈1.41, ≈1.73)23. 如图, 是 的外接圆, 是 的直径, .
(1)、求出A与C之间的距离AC .(2)、已知距观测点D处100海里范围内有暗礁.若巡逻船A沿直线AC去营救船C , 在去营救的途中有无触暗礁危险?(参考数据: ≈1.41, ≈1.73)23. 如图, 是 的外接圆, 是 的直径, .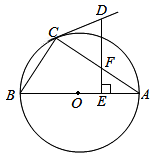 (1)、求证: 是 的切线;(2)、若 ,垂足为 交 于点 ,求 的长.24. 已知抛物线y=ax2+bx+c经过A(2,0),B(3n﹣4,y1),C(5n+6,y2)三点,对称轴是直线x=1.关于x的方程ax2+bx+c=x有两个相等的实数根.(1)、求抛物线的解析式;(2)、若n<﹣5,试比较y1与y2的大小;(3)、若B,C两点在直线x=1的两侧,且y1>y2 , 求n的取值范围.25. 如图,在正方形ABCD中,点E是边AB上的一个动点(点E与点A , B不重合),连接CE , 过点B作BF⊥CE于点G , 交AD于点F .
(1)、求证: 是 的切线;(2)、若 ,垂足为 交 于点 ,求 的长.24. 已知抛物线y=ax2+bx+c经过A(2,0),B(3n﹣4,y1),C(5n+6,y2)三点,对称轴是直线x=1.关于x的方程ax2+bx+c=x有两个相等的实数根.(1)、求抛物线的解析式;(2)、若n<﹣5,试比较y1与y2的大小;(3)、若B,C两点在直线x=1的两侧,且y1>y2 , 求n的取值范围.25. 如图,在正方形ABCD中,点E是边AB上的一个动点(点E与点A , B不重合),连接CE , 过点B作BF⊥CE于点G , 交AD于点F .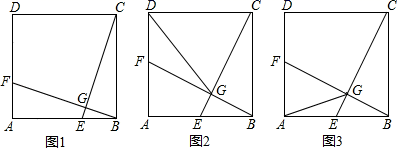 (1)、如图1,若BE=1,则AF=;(2)、如图2,当点E运动到AB中点时,连接DG , 求证:DC=DG;(3)、如图3,若AB=4,连接AG , 当点E在边AB上运动的过程中.AG是否存在最小值,若存在求出AG最小值,并求出此时AE的值;若不存在,请说明理由.
(1)、如图1,若BE=1,则AF=;(2)、如图2,当点E运动到AB中点时,连接DG , 求证:DC=DG;(3)、如图3,若AB=4,连接AG , 当点E在边AB上运动的过程中.AG是否存在最小值,若存在求出AG最小值,并求出此时AE的值;若不存在,请说明理由.