山东省临沂市河东区2021年中考数学二模试卷
试卷更新日期:2021-06-25 类型:中考模拟
一、单选题
-
1. 在0,1, ,-1四个数中,最小的数是( )A、0 B、1 C、 D、-12. 斑叶兰被列为国家二级保护植物,它的一粒种子重约0.0000005克.将0.0000005用科学记数法表示为( )
A、5×107 B、5×10﹣7 C、0.5×10﹣6 D、5×10﹣63. 将一把直尺和一块含30°和60°角的三角板ABC按如图所示的位置放置,如果∠CDE=40°,那么∠BAF的大小为( )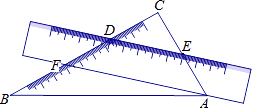 A、10° B、15° C、20° D、25°4. 用配方法解方程 ,配方后所得方程是( )A、 B、 C、 D、5. 把不等式组 中每个不等式的解集在同一条数轴上表示出来,正确的为( )A、
A、10° B、15° C、20° D、25°4. 用配方法解方程 ,配方后所得方程是( )A、 B、 C、 D、5. 把不等式组 中每个不等式的解集在同一条数轴上表示出来,正确的为( )A、 B、
B、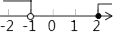 C、
C、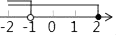 D、
D、 6. 为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理,她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E,标记好脚掌中心位置为B,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C距离旗杆底部D的距离为4m,如图所示.已知小丽同学的身高是1.54m,眼睛位置A距离小丽头顶的距离是4cm,则旗杆DE的高度等于( )
6. 为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理,她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E,标记好脚掌中心位置为B,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C距离旗杆底部D的距离为4m,如图所示.已知小丽同学的身高是1.54m,眼睛位置A距离小丽头顶的距离是4cm,则旗杆DE的高度等于( ) A、10m B、12m C、12.4m D、12.32m7. 一个几何体的三视图如左图所示,则该几何体是( )
A、10m B、12m C、12.4m D、12.32m7. 一个几何体的三视图如左图所示,则该几何体是( )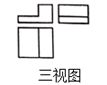 A、
A、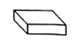 B、
B、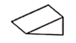 C、
C、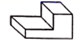 D、
D、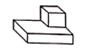 8. 如图,随机闭合开关 , , 中的两个,则能让两盏灯泡同时发光的概率为( )
8. 如图,随机闭合开关 , , 中的两个,则能让两盏灯泡同时发光的概率为( )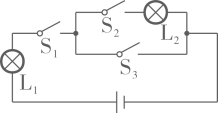 A、 B、 C、 D、9. 某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106](即96≤净重≤106),样本数据分组为[96,98)(即96≤净重<98)以下类似,[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是 ( ).
A、 B、 C、 D、9. 某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106](即96≤净重≤106),样本数据分组为[96,98)(即96≤净重<98)以下类似,[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是 ( ).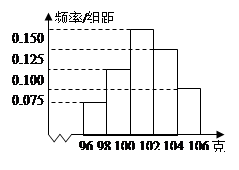
A、90 B、75 C、 60 D、4510. 为了缓解城市用水紧张及提倡节约用水,某市自2021年1月1日起调整居民用水价格,每立方米水费上涨25%,该市林老师家2020年12月份的水费是18元,而2021年1月份的水费是36元,且已知林老师家2021年1月份的用水量比2020年12月份的用水量多3m3 , 求该市去年的居民用水价格?设去年的居民用水价格x元/m3 , 则所列方程正确的是( )A、 B、 C、 D、11. 如图,在△ABC中,∠ACB=90°,BC=a,AC=b.以点B为圆心,BC的长为半径画弧,交线段AB于点D,以点A为圆心,AD长为半径画弧,交线段AC于点E.下列哪条线段的长度是方程x2+2ax-b2=0的一个根( ) A、线段AD的长 B、线段BC的长 C、线段EC的长 D、线段AC的长12. 设 , 是方程 的两根,则 的值是( )A、0 B、1 C、2000 D、400000013. 如图,反比例函数 的图象经过矩形OABC对角线的交点M , 分别与AB、BC相交于点D、E . 若四边形ODBE的面积为6,则k的值为( )
A、线段AD的长 B、线段BC的长 C、线段EC的长 D、线段AC的长12. 设 , 是方程 的两根,则 的值是( )A、0 B、1 C、2000 D、400000013. 如图,反比例函数 的图象经过矩形OABC对角线的交点M , 分别与AB、BC相交于点D、E . 若四边形ODBE的面积为6,则k的值为( )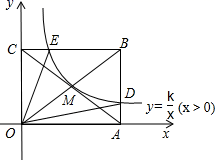 A、 B、 C、2 D、14. 图,正方形 中, E为 的中点, 于M,交 于点N,交 于点F,连接 、 .有如下结论:① ;② ;③ ;④ ;⑤ .其中正确的结论的个数为( )
A、 B、 C、2 D、14. 图,正方形 中, E为 的中点, 于M,交 于点N,交 于点F,连接 、 .有如下结论:① ;② ;③ ;④ ;⑤ .其中正确的结论的个数为( )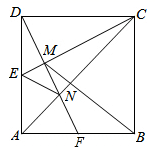 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
15. 若 , ,则代数式 的值为 .16. 已知关于x的一元二次方程 有两个不相等的实数根,则m的取值范围是17.
如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,则BC的长是 .
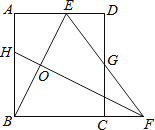 18. 如图,放置在直线l上的扇形OAB , 由①图滚动(无滑动)到图②,在由图②滚动到图③,若半径OA=2,∠AOB=45°,则点O的路径长为 .
18. 如图,放置在直线l上的扇形OAB , 由①图滚动(无滑动)到图②,在由图②滚动到图③,若半径OA=2,∠AOB=45°,则点O的路径长为 .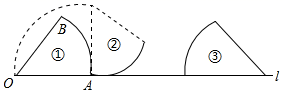 19. 如图,在平面直角坐标系中,点A在一次函数 位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD , 且 , ,则OD的最大值是 .
19. 如图,在平面直角坐标系中,点A在一次函数 位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD , 且 , ,则OD的最大值是 .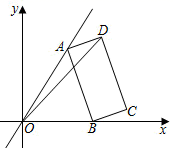
三、解答题
-
20. 计算: .21. 2020年初我国新冠肺炎疫情牵动全国人民的心某社区积极组织社区居民为疫情地区的人民献爱心活动为了解该社区居民捐款情况,对社区部分捐款户数进行分组统计(统计表如下),数据整理成如图所示的不完整统计图已知A、B两组捐款户数直方图的高度比为1:5,请结合图中相关数据回答下列问题.
捐款分组统计表
组别
捐款额(x)元
A
B
C
D
E
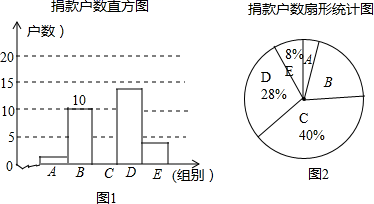 (1)、A组的频数是多少?本次调查样本的容量是多少?(2)、求出C组的频数并补全直方图;(3)、若该社区有500户住户,请估计捐款不少于300元的户数是多少?22. 如图所示,某人在山坡坡脚A处测得电视塔尖点C 的仰角为60°,沿山坡向上走到P处再测得C的仰角为45°,已知OA=200米,山坡坡度为 (即tan∠PAB= ),且O、A、B在同一条直线上,求电视塔OC的高度以及此人所在位置点P的垂直高度.(测倾器的高度忽略不计,结果保留根号)
(1)、A组的频数是多少?本次调查样本的容量是多少?(2)、求出C组的频数并补全直方图;(3)、若该社区有500户住户,请估计捐款不少于300元的户数是多少?22. 如图所示,某人在山坡坡脚A处测得电视塔尖点C 的仰角为60°,沿山坡向上走到P处再测得C的仰角为45°,已知OA=200米,山坡坡度为 (即tan∠PAB= ),且O、A、B在同一条直线上,求电视塔OC的高度以及此人所在位置点P的垂直高度.(测倾器的高度忽略不计,结果保留根号)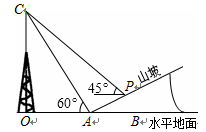 23. 如图,在⊙O中,AB为直径,AC为弦.过BC延长线上一点G,作GD⊥AO于点D,交AC于点E,交⊙O于点F,M是GE的中点,连接CF,CM.
23. 如图,在⊙O中,AB为直径,AC为弦.过BC延长线上一点G,作GD⊥AO于点D,交AC于点E,交⊙O于点F,M是GE的中点,连接CF,CM.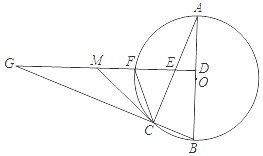 (1)、判断CM与⊙O的位置关系,并说明理由;(2)、若∠ECF=2∠A,CM=6,CF=4,求MF的长.24. 为鼓励大学生毕业后自主创业,我市出台了相关政策:由政府协调,本市企业按成本价提供产品给应届毕业生自主销售,成本价与出厂价之间的差价由政府承担.赵某按照相关政策投资销售本市生产的一种新型“儿童玩具枪”.已知这种“儿童玩具枪”的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=−10x+500.(1)、赵某在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?(2)、设赵某获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润?(3)、物价部门规定,这种“儿童玩具枪”的销售单价不得高于28元.如果赵某想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?25. 如图,矩形ABCD中,已知AB=6.BC=8,点E是射线BC上的一个动点,连接AE并延长,交射线DC于点F . 将△ABE沿直线AE翻折,点B的对应点为点B'.
(1)、判断CM与⊙O的位置关系,并说明理由;(2)、若∠ECF=2∠A,CM=6,CF=4,求MF的长.24. 为鼓励大学生毕业后自主创业,我市出台了相关政策:由政府协调,本市企业按成本价提供产品给应届毕业生自主销售,成本价与出厂价之间的差价由政府承担.赵某按照相关政策投资销售本市生产的一种新型“儿童玩具枪”.已知这种“儿童玩具枪”的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=−10x+500.(1)、赵某在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?(2)、设赵某获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润?(3)、物价部门规定,这种“儿童玩具枪”的销售单价不得高于28元.如果赵某想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?25. 如图,矩形ABCD中,已知AB=6.BC=8,点E是射线BC上的一个动点,连接AE并延长,交射线DC于点F . 将△ABE沿直线AE翻折,点B的对应点为点B'.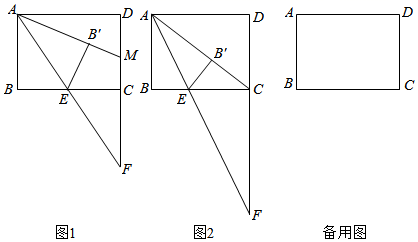 (1)、如图1,若点E为线段BC的中点,延长AB'交CD于点M , 求证:AM=FM;(2)、如图2,若点B'恰好落在对角线AC上,求 的值;(3)、若 = ,求∠DAB'的正弦值.26. 已知抛物线 ( 为常数, )经过点 ,点 是 轴正半轴上的动点.(1)、当 时,求抛物线的顶点坐标;(2)、点 在抛物线上,当 , 时,求 的值;(3)、点 在抛物线上,当 的最小值为 时,求 的值.
(1)、如图1,若点E为线段BC的中点,延长AB'交CD于点M , 求证:AM=FM;(2)、如图2,若点B'恰好落在对角线AC上,求 的值;(3)、若 = ,求∠DAB'的正弦值.26. 已知抛物线 ( 为常数, )经过点 ,点 是 轴正半轴上的动点.(1)、当 时,求抛物线的顶点坐标;(2)、点 在抛物线上,当 , 时,求 的值;(3)、点 在抛物线上,当 的最小值为 时,求 的值.