山东省济宁市任城区2021年中考数学二模试卷

试卷更新日期：2021-06-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中，绝对值最大的数是（　　）

A、5 B、﹣3 C、0 D、﹣2

查看试题解析
2. 下列所述图形中，既是中心对称图形，又是轴对称图形的是（　　）

A、矩形 B、平行四边形 C、正五边形 D、正三角形

查看试题解析
3. 下列计算正确的是（　　）

A、x÷x⁴＝x¹¹ B、（a³）²＝a⁵ C、 $2 \sqrt{2} +3 \sqrt{3} =5 \sqrt{5}$ D、 $\sqrt{6} \div \sqrt{3} = \sqrt{2}$

查看试题解析
4. 有一组数据：3，4，5，6，6，则这组数据的平均数、众数、中位数分别是（　　）

A、4.8，6，6 B、5，5，5 C、4.8，6，5 D、5，6，6

查看试题解析
5. 化简 $\frac{m^{2}}{m - 3} - \frac{9}{m - 3}$ 的结果是（）

A、m+3 B、m﹣3 C、 $\frac{m - 3}{m + 3}$ D、 $\frac{m + 3}{m - 3}$

查看试题解析
6. 如图，AB∥CD，AD＝CD，∠1＝70°，则∠2的度数是（）

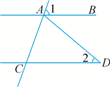A、20° B、35° C、40° D、70°

查看试题解析
7. 如图，某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心，AB为半径的扇形(忽略铁丝的粗细)，则所得的扇形DAB的面积为（）

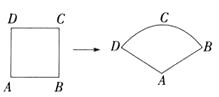A、6 B、7 C、8 D、9

查看试题解析
8. 《九章算术》是中国古代的数学专著，下面这道题是《九章算术》中第七章的一道题：“今有共买物，人出八，盈三；人出七，不足四，问人数、物价各几何？”译文：“几个人一起去购买某物品，如果每人出8钱，则多了3钱；如果每人出7钱，则少了4钱．问有多少人，物品的价格是多少？”设有x人，物品价格为y钱，可列方程组为（）

A、 ${\begin{array}{l} 8 x - 3 = y \\ 7 x + 4 = y \end{array}$ B、 ${\begin{array}{l} y - 8 x = 3 \\ y - 7 x = 4 \end{array}$ C、 ${\begin{array}{l} 8 x - y = 3 \\ 7 x - y = 4 \end{array}$ D、 ${\begin{array}{l} 8 x + 3 = y \\ 7 x - 4 = y \end{array}$

查看试题解析
9. 如图，在矩形ABCD中，AD＝ $\sqrt{2}$ AB ， ∠BAD的平分线交BC于点E ， DH⊥AE于点H ，连接BH并延长交CD于点F ，连接DE交BF于点O ，下列结论：①∠AED＝∠CED；②OE＝OD；③BH＝HF；④AB＝HF ，其中正确的有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 记s_n＝a₁+a₂+…+a_n ，令T_n＝ $\frac{S_{1} + S_{2} + \dots + S_{n}}{n}$ ，则T_n为a₁+a₂+…+a_n这列数的“凯森和”．已知a₁+a₂+…+a₅₀₀的“凯森和”为2004，那么18，a₁+a₂+…+a₅₀₀的“凯森和”为（　　）

A、2018 B、2019 C、2020 D、2021

查看试题解析

二、填空题

11. 已知a+b=3，a-b=5，则代数式a²-b²的值是.

查看试题解析
12. 如图，在Rt△ABC中，∠C＝90°，以顶点A为圆心，适当长为半径画弧，分别交AB，AC于点N，M，再分别以点M，N为圆心，大于MN长为半径画弧，两弧交于点P，射线AP交边BC于点D，若△DAC∽△ABC，则∠B＝度．

查看试题解析
13. 从甲、乙、丙、丁4名三好学生中随机抽取2名学生担任升旗手，则抽取的2名学生是甲和乙的概率为 .

查看试题解析
14. 如图，5个边长相等的小正方形拼成一个平面图形，小丽手中还有1个同样的小正方形，她想将它与图中的平面图形拼接在一起，从而可以构成一个正方体的平面展开图，则小丽总共能有种拼接方法.

查看试题解析
15. 如图，在直角坐标系中，已知点B（8，0），等边三角形OAB的顶点A在反比例函数y＝ $\frac{k}{x}$ 的图象上：如果把△OAB向右平移a个单位长度，对应得到△O'A'B'，当这个函数图象经过△O'A'B'一边的中点时，则a＝．

查看试题解析

三、解答题

16. 计算： ${(- 1)}^{2021} + {(\frac{1}{3})}^{- 1} + | - \sqrt{2} | - 2 \sin 45 °$ ．

查看试题解析
17. 4月23日是“世界读书日”，学校开展“让书香溢满校园”读书活动，以提升青少年的阅读兴趣，九年级(1)班数学活动小组对本年级600名学生每天阅读时间进行了统计，

根据所得数据绘制了如图所示的两幅不完整的统计图(每组包括最小值不包括最大值)．九年级(1)班每天阅读时间在0.5 h以内的学生占全班人数的8%，根据统计图解答下列问题：

(1)、九年级(1)班有名学生．

(2)、补全频数分布直方图．

(3)、除九年级(1)班外，九年级其他班级每天阅读时间为1～1.5 h的学生有165人，请你补全扇形统计图．

(4)、求该年级每天阅读时间不少于1 h的学生有多少人．

查看试题解析
18. 如图，小明家小区空地上有两颗笔直的树CD、EF．一天，他在A处测得树顶D的仰角∠DAC=30°，在B处测得树顶F的仰角∠FBE=45°，线段BF恰好经过树顶D．已知A、B两处的距离为2米，两棵树之间的距离CE=3米，A、B、C、E四点在一条直线上，求树EF的高度．
（ $\sqrt{3}$ ≈1.7， $\sqrt{2}$ ≈1.4，结果保留一位小数）

查看试题解析
19. 某市某水果批发市场某批发商原计划以每千克10元的单价对外批发销售某种水果．为了加快销售，该批发商对价格进行两次下调后，售价降为每千克6.4元．

(1)、求平均每次下调的百分率；

(2)、某大型超市准备到该批发商处购买2吨该水果，因数量较多，该批发商决定再给予两种优惠方案以供选择．方案一：打八折销售；方案二：不打折，每吨优惠现金1000元．试问超市采购员选择哪种方案更优惠？请说明理由．

查看试题解析
20. 如图， $Δ$ ABC内接于圆O ， ∠B＝60°，过c作圆O的切线l ，与直径AD的延长线交于点E ， AF⊥l ，垂足为F ．

(1)、求证：AC平分∠FAD；

(2)、已知AF＝3 $\sqrt{3}$ ，求阴影部分面积．

查看试题解析
21. 在平面直角坐标系xOy中，抛物线C：y=mx²+4x+1．

(1)、当抛物线C经过点A（-5，6）时，求抛物线的表达式及顶点坐标；

(2)、当直线y=-x+l与直线y=x+3关于抛物线C的对称轴对称时，求m的值；

(3)、若抛物线C：y=mx²+4x+l（m＞0）与x轴的交点的横坐标都在-l和0之间（不包括-l和0）．结合函数的图象，求m的取值范围．

查看试题解析
22. 如果一个三角形有一条边上的高等于这条边的一半，那么我们把这个三角形叫做“半高三角形”．这条高称为“半高”．如图1，对于△ABC ， BC边上的高AD等于BC的一半，△ABC就是“半高三角形”．此时，称△ABC是“BC边半高三角形”，AD是“BC边半高”；如图2，对于△EFG ， EF边上的高GH等于EF的一半，△EFG就是半高三角形，此时，称△EFG是EF边半高三角形，CH是“EF边半高”．

(1)、在Rt△ABC中，∠ACB＝90°，AB＝10cm，若△ABC是“BC边半高三角形”，则AC＝cm；

(2)、若一个三角形既是等腰三角形又是半高三角形，且“半高”长为2cm，则该等腰三角形底边长的所有可能值为．

(3)、如图3，平面直角坐标系内，直线y＝x+2与抛物线y＝x²交于R ， S两点，点P是抛物线y＝x².上的一个动点，点Q是坐标系内一点，且使得△RSQ为“RS边半高三角形”当点P介于抛物线上点R与点S之间，且PQ取得最小值时，求点P的坐标．

查看试题解析