山东省济南市南山区2021年中考数学二模试卷

试卷更新日期：2021-06-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中，2的相反数是（　　）

A、2 B、﹣2 C、 $\frac{1}{2}$ D、﹣ $\frac{1}{2}$

查看试题解析
2. 如图，是由5个大小相同的小立方块搭成的几何体，其主视图是（）

A、 B、 C、 D、

查看试题解析
3. 2021年2月27日，由嫦娥五号带回的月球样品（月壤）正式入藏中国国家博物馆，盛放月球样品的容器整体造型借鉴自国家博物馆馆藏的系列青铜“尊”造型，以体现稳重大方之感，它的容器整体外部造型高 $38.44 cm$ ，象征地球与月亮的平均间距约 $384400 km$ ．将384400用科学记数法表示应为（）

A、 $38.44 \times 10^{4}$ B、 $3.844 \times 10^{5}$ C、 $3.844 \times 10^{4}$ D、 $0.3844 \times 10^{6}$

查看试题解析
4. 剪纸是我国传统的民间艺术，下列剪纸作品中既是轴对称图形，也是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
5. 某班班长统计去年1∼8月“书香校园”活动中全班同学的课外阅读数量(单位：本)，绘制了如图折线统计图，下列说法正确的是（）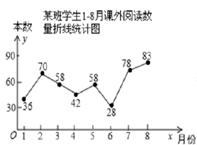

A、每月阅读数量的平均数是50 B、众数是42 C、中位数是58 D、每月阅读数量超过40的有4个月

查看试题解析
6. 下列运算结果正确的是（）

A、a²•a³=a⁶ B、﹣（a﹣b）=﹣a+b C、a²+a²=2a⁴ D、a⁸÷a⁴=a²

查看试题解析
7. 如图，A、B的坐标分别为（﹣2，1）、（0，﹣2）．若将线段AB平移至A₁B₁ ， A₁、B₁的坐标分别为（a ， 4）、（3，b），则a+b的值为（　　）

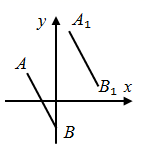A、2 B、3 C、4 D、5

查看试题解析
8. 如图，函数y₁＝﹣2x 与 y₂＝ax+3 的图象相交于点 A（m，2），则关于 x 的不等式﹣2x＞ax+3 的解集是（）

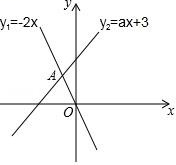A、x＞2 B、x＜2 C、x＞﹣1 D、x＜﹣1

查看试题解析
9. 春节期间，某老师读到《行路难》中“闲来垂钓碧溪上，忽复乘舟梦日边．”邀约好友一起在江边垂钓，如图，河堤AB的坡度为1∶2.4，AB长为5.2米，钓竿AC与水平线的夹角是60°，其长为6米，若钓竿AC与钓鱼线CD的夹角也是60°，则浮漂D与河堤下端B之间的距离约为（参考数据： $\sqrt{3} \approx 1.732$ ）（）

A、2.33米 B、2.35米 C、2.36米 D、2.42米

查看试题解析
10. 如图，在矩形ABCD中，点E是边BC的中点，AE⊥BD，垂足为F，则tan∠BDE的值是（）

A、 $\frac{\sqrt{2}}{4}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{\sqrt{2}}{3}$

查看试题解析
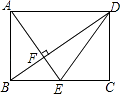11. 在平面直角坐标系xOy中，已知点M，N的坐标分别为（﹣1，2），（2，1），若抛物线y=ax²﹣x+2（a≠0）与线段MN有两个不同的交点，则a的取值范围是（）

A、a≤﹣1或 $\frac{1}{4}$ ≤a＜ $\frac{1}{3}$ B、 $\frac{1}{4}$ ≤a＜ $\frac{1}{3}$ C、a≤ $\frac{1}{4}$ 或a＞ $\frac{1}{3}$ D、a≤﹣1或a≥ $\frac{1}{4}$

查看试题解析

二、填空题

12. 因式分解：a²﹣16b²＝．

查看试题解析
13. 转盘中6个扇形的面积相等，任意转动转盘一次，当转盘停止转动，指针落在扇形中的数为3的倍数的概率是．

查看试题解析
14. 代数式 $\frac{1}{x + 3}$ 与代数式 $\frac{3}{x}$ 的值相等，则x＝．

查看试题解析
15. 正多边形的一个外角是 $72^{o}$ ，则这个多边形的内角和的度数是．

查看试题解析
16. 如图，正方形ABCD的边长为4，点E在BC上，四边形EFGB也是正方形，以B为圆心，BA长为半径画 $\overset{⌢}{AC}$ ，连结AF，CF，则图中阴影部分面积为．

查看试题解析
17. 如图，在Rt△ABC中，∠BAC＝90°，AB＝2，AC＝3，点P为BC边上一动点，PE⊥AB于点E ， PF⊥AC于点F ，连接EF ，点M为EF的中点，则AM的最小值为．

查看试题解析

三、解答题

18. 计算：|﹣ $\sqrt{2}$ |﹣（ $\frac{1}{3}$ ）^﹣1+（2021﹣π）⁰﹣2cos45°．

查看试题解析
19. 解不等式组： ${\begin{matrix} 3 (x + 1) > x - 1 \\ \frac{x + 7}{2} \geq 2 x - 1 \end{matrix}$ ．并写出所有的正整数解．

查看试题解析
20. 如图，E，F为平行四边形ABCD的对角线BD上的两点，AE⊥BD于点E，CF⊥BD于点F．

求证：AE=CF．

查看试题解析
21. 初三年级教师对试卷讲评课中学生参与的深度与广度进行评价调查，其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项．评价组随机抽取了若干名初中学生的参与情况，绘制成如图所示的条形统计图和扇形统计图（均不完整），请根据图中所给信息解答下列问题：

(1)、在这次评价中，一共抽查了名学生；

(2)、在扇形统计图中，项目“主动质疑”所在的扇形的圆心角的度数为度；

(3)、请将条形统计图补充完整；

(4)、如果全市有6000名初三学生，那么在试卷评讲课中，“独立思考”的初三学生约有多少人？

查看试题解析
22. 如图， $△ A B C$ 中， $∠ C = 90 °$ ，点E在 $A B$ 上，以 $B E$ 为直径的 $⊙ O$ 与 $A C$ 相切于点D ，与 $B C$ 相交于点F ，连接 $B D ， D E$ ．

(1)、求证： $∠ A D E = ∠ D B E$ ；

(2)、若 $\sin A = \frac{3}{5} ， B C = 6$ ，求 $⊙ O$ 的半径．

查看试题解析
23. 某校为美化校园，计划对面积为1800m²的区域进行绿化，安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍，并且在独立完成面积为400 m²区域的绿化时，甲队比乙队少用4天.

(1)、求甲、乙两工程队每天能完成绿化的面积分别是多少m²？

(2)、若学校每天需付给甲队的绿化费用是0.4万元，乙队为0.25万元，要使这次的绿化总费用不超过8万元，至少应安排甲队工作多少天？

查看试题解析
24. 如图，一次函数y＝mx+1的图象与反比例函数y＝ $\frac{k}{x}$ 的图象相交于A、B两点，点C在x轴正半轴上，点D(1，﹣2)，连结OA、OD、DC、AC，四边形OACD为菱形．

(1)、求一次函数与反比例函数的解析式；

(2)、根据图象，直接写出反比例函数的值小于2时，x的取值范围；

(3)、设点P是直线AB上一动点，且 $S_{△ O A P}$ ＝ $\frac{1}{2}$ S_菱形OACD ，求点P的坐标．

查看试题解析
25.

(1)、（问题探究）
如图1，△ABC和△DEC均为等腰直角三角形，∠ACB＝∠DCE＝90°，点B ， D ， E在同一直线上，连接AD ， BD ．

①请探究AD与BD之间的位置关系？并加以证明．

②若AC＝BC＝ $\sqrt{10}$ ，DC＝CE＝ $\sqrt{2}$ ，求线段AD的长．

(2)、（拓展延伸）
如图2，△ABC和△DEC均为直角三角形，∠ACB＝∠DCE＝90°，AC＝ $\sqrt{21}$ ，BC＝ $\sqrt{7}$ ，CD＝ $\sqrt{3}$ ，CE＝1．将△DCE绕点C在平面内顺时针旋转，设旋转角∠BCD为α（0°≤α＜360°），作直线BD ，连接AD ，当点B ， D ， E在同一直线上时，画出图形，并求线段AD的长．

查看试题解析
26. 如图，已知抛物线y＝ax²+bx﹣3的图象与x轴交于点A（1，0）和B（3，0），与y轴交于点C，D是抛物线的顶点，对称轴与x轴交于E.

(1)、求抛物线的解析式；

(2)、如图1，在抛物线的对称轴DE上求作一点M，使△AMC的周长最小，并求出点M的坐标和周长的最小值.

(3)、如图2，点P是x轴上的动点，过P点作x轴的垂线分别交抛物线和直线BC于F、G，使△FCG是等腰三角形，直接写出P的横坐标.

查看试题解析