山东省菏泽市牡丹区2021年中考数学二模试卷

试卷更新日期：2021-06-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中，比3大比4小的无理数是（）

A、3.14 B、 $\frac{10}{3}$ C、 $\sqrt{12}$ D、 $\sqrt{17}$

查看试题解析
2. 目前世界上刻度最小的标尺是钻石标尺，它的最小刻度为 $0.2 nm$ （其中 $1 nm = 10^{- 9} m$ ），用科学记数法表示这个最小刻度（单位：m），结果是（）

A、 $2 \times 10^{- 8} m$ B、 $2 \times 10^{- 9} m$ C、 $2 \times 10^{- 10} m$ D、 $2 \times 10^{- 11} m$

查看试题解析
3. 如图所示的几何体，它的左视图是（　　）

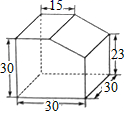A、 B、 C、 D、

查看试题解析
4. 如图，长方形ABCD中∠DAC＝68°，请依据尺规作图的痕迹，求出∠α等于（）

A、34° B、44° C、56° D、68°

查看试题解析
5. 当 $b + c = 5$ 时，关于 $x$ 的一元二次方程 $3 x^{2} + b x - c = 0$ 的根的情况为（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定

查看试题解析
6. 如图，AB是⊙O的直径，直线DE与⊙O相切于点C，过A，B分别作AD⊥DE，BE⊥DE，垂足为点D，E，连接AC，BC，若AD＝ $\sqrt{3}$ ，CE＝3，则 $\overset{⌢}{A C}$ 的长为（　　）

A、 $\frac{2 \sqrt{3}}{3}$ B、 $\frac{\sqrt{3}}{3}$ π C、 $\frac{\sqrt{3}}{2}$ π D、 $\frac{2 \sqrt{3}}{3}$ π

查看试题解析
7. 如图，已知 $Δ A_{1} O B_{1}$ 与 $Δ A_{2} O B_{2}$ 位似，且 $Δ A_{1} O B_{1}$ 与 $Δ A_{2} O B_{2}$ 的周长之比为1：2，点 $A_{1}$ 的坐标为 $(- 1 ， 2)$ ，则点 $A_{2}$ 的坐标为（）

A、 $(1 ， - 4)$ B、 $(2 ， - 4)$ C、 $(- 4 ， 2)$ D、 $(- \sqrt{2} ， 1)$

查看试题解析
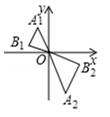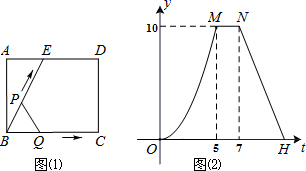8. 如图（1）所示，E为矩形 $A B C D$ 的边 $A D$ 上一点，动点 $P ， Q$ 同时从点B出发，点P沿折线 $B E - E D - D C$ 运动到点C时停止，点Q沿 $B C$ 运动到点C时停止，它们运动的速度都是 $1 cm$ /秒．设 $P 、 Q$ 同时出发t秒时， $△ B P Q$ 的面积为 $y {cm}^{2}$ ．已知y与t的函数关系图象如图（2）（曲线 $O M$ 为抛物线的一部分），则下列结论：① $A D = B E = 5$ ；② $\cos ∠ A B E = \frac{3}{5}$ ；③当 $0 < t \leq 5$ 时， $y = \frac{2}{5} t^{2}$ ；④当 $t = \frac{29}{4}$ 秒时， $△ A B E \sim △ Q B P$ ；其中正确的结论是（　　）

A、①②③ B、①③ C、①③④ D、②④

查看试题解析

二、填空题

9. 分解因式： $a x^{2} - 6 a x y + 9 a y^{2} =$ .

查看试题解析
10. 已知x，y都是实数，且y＝ $\sqrt{x - 3}$ + $\sqrt{3 - x}$ ﹣2，则y^x＝．

查看试题解析
11. 若关于x的方程 $\frac{2}{x - 2} + \frac{x + m}{2 - x} = 2$ 有增根，则m的值是

查看试题解析
12. 如图，菱形 $O A B C$ 中， $A B = 4$ ， $∠ A O C = 30 °$ ， $O B$ 所在直线为反比例函数 $y = \frac{k}{x}$ 的对称轴，当反比例函数 $y = \frac{k}{x} (x < 0)$ 的图象经过 $A 、 C$ 两点时，k的值为.

查看试题解析
13. 如图，在矩形 $A B C D$ 中， $A B = 3$ ， $B C = 4$ ，点P为 $A B$ 边上一点，将 $△ A P B$ 沿 $P B$ 翻折，点A落在点 $A^{'}$ 处，当点 $A^{'}$ 在矩形的对角线上时， $A P$ 的长度为．

查看试题解析
14. 如图， $∠ M O N = 60 °$ ，点 $A_{1}$ 在射线 $O N$ 上，且 $O A_{1} = 1$ ，过点 $A_{1}$ 作 $A_{1} B_{1} ⊥ O N$ 交射线 $O M$ 于点 $B_{1}$ ，在射线 $O N$ 上截取 $A_{1} A_{2}$ ，使得 $A_{1} A_{2} = A_{1} B_{1}$ ；过点 $A_{2}$ 作 $A_{2} B_{2} ⊥ O N$ 交射线 $O M$ 于点 $B_{2}$ ，在射线 $O N$ 上截取 $A_{2} A_{3}$ ，使得 $A_{2} A_{3} = A_{2} B_{2}$ ；……；按照此规律进行下去，则 $A_{2021} B_{2021}$ 长为．

查看试题解析

三、解答题

15. 计算： $4 \sin 60 ° - | 1 - \sqrt{3} | + {(\frac{1}{3})}^{- 1} + \sqrt[3]{- 27}$ ．

查看试题解析
16. 先化简，再求值： $\frac{x^{2} - 4 x + 4}{x + 1} \div (\frac{3}{x + 1} - x + 1)$ ，请从不等式组 ${\begin{matrix} 7 - 3 x \geq 1 \\ 2 x + 7 \geq 3 \end{matrix}$ 的整数解中选择一个合适的值代入求值．

查看试题解析
17. 已知：如图，在矩形ABCD中，点E在边AD上，点F在边BC上，且AE＝CF ，点G ， H在对角线BD上，且BG＝DH ．

(1)、求证：△BFH≌△DEG；

(2)、连接DF ，若DF＝BF ，则四边形EGFH是什么特殊四边形？证明你的结论．

查看试题解析
18.
如图，在路边安装路灯，灯柱BC高15m，与灯杆AB的夹角ABC为120°．路灯采用锥形灯罩，照射范围DE长为18.9m，从D、E两处测得路灯A的仰角分别为∠ADE=80.5°，∠AED=45°．求灯杆AB的长度．（参考数据：cos80.5°≈0.2，tan80.5°≈6.0）

查看试题解析
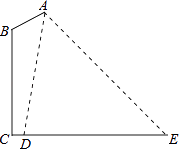19. 第30届菏泽国际牡丹文化旅游节于4月1日至5月10日举办，主题为“赞盛世牡丹，品魅力菏泽”．为了宣传牡丹制品，某商店欲购进 $A ， B$ 两种牡丹制品，若购进A种牡丹制品5件，B种牡丹制品3件，共需450元；若购进A种牡丹制品10件，B种牡丹制品8件，共需1000元．

(1)、购进 $A ， B$ 两种牡丹制品每件各需多少元？

(2)、该商店购进足够多的 $A ， B$ 两种牡丹制品，在销售中发现，A种牡丹制品售价为每件80元，每天可销售100件，现在决定对A种牡丹制品在每件80元的基础上降价销售，每件每降价1元，多售出20件，该商店对A种牡丹制品降价销售后每天销量超过200件；B种牡丹制品销售状况良好，每天可获利7000元，为使销售 $A ， B$ 两种牡丹制品每天总获利为10000元，A种牡丹制品每件降价多少元？

查看试题解析
20. 如图，在平面直角坐标系中，将一块等腰直角三角板ABC放在第二象限，斜靠在两坐标轴上，点C坐标为（-1，0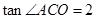），．一次函数 $y = k x + b$ 的图象经过点B、C ，反比例函数 $y = \frac{m}{x}$ 的图象经过点B．

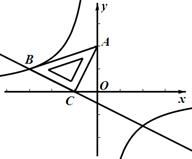(1)、求一次函数和反比例函数的关系式；

(2)、直接写出当x＜0时， $k x + b - \frac{m}{x} < 0$ 的解集；

(3)、在x轴上找一点M ，使得AM+BM的值最小，并求出点M的坐标和AM+BM的最小值．

查看试题解析
21. “校园安全”受到全社会的关注，菏泽市某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图，请你根据统计图中所提供的信息解答下列问题：

(1)、接受问卷调查的学生共有人，扇形统计图中“基本了解”部分所对应扇形的圆心角为°；

(2)、请补全条形统计图；

(3)、若该中学共有学生900人，请根据上述调查结果，估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数；

(4)、若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛，请用树状图或列表法求出恰好抽到1个男生和1个女生的概率．

查看试题解析
22. 如图，在 $△$ ABC中，∠C=90°．∠ABC的平分线交AC于点E ，点F在AB上，以BF为直径的⊙O恰好经过点E ．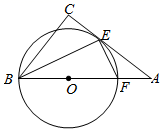

(1)、求证：AC是⊙O的切线；

(2)、若AE=2AF=4，求BC的长．

查看试题解析
23. 已知：如图1所示将一块等腰三角板BMN放置与正方形ABCD的 $∠ B$ 重合，连接AN、CM，E是AN的中点，连接BE．

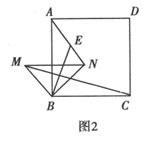(1)、（观察猜想）
CM与BE的数量关系是；CM与BE的位置关系是；

(2)、（探究证明）
如图2所示，把三角板BMN绕点B逆时针旋转 $α (0 < α < 90)$ ，其他条件不变，线段CM与BE的关系是否仍然成立，并说明理由；

(3)、（拓展延伸）
若旋转角 $α = 45^{\circ}$ ，且 $∠ N B E = 2 ∠ A B E$ ，求 $\frac{B C}{B N}$ 的值．

查看试题解析
24. 如图，抛物线y＝﹣x²+bx+c与x轴交于点A（﹣1，0）和B（3，0），与y轴交于点C

(1)、求抛物线的表达式；

(2)、如图1，若点F在线段OC上，且OF＝OA ，经入过点F的直线在第一象限内与抛物线交于点D ，与线段BC交于点E ，求 $\frac{D E}{E F}$ 的最大值；

(3)、如图2，若P为抛物线的顶点，动点Q在抛物线上，当∠QCO＝∠PBC时，请直接写出点Q的坐标．

查看试题解析