山东省菏泽市鄄城县2021年中考数学一模试卷
试卷更新日期:2021-06-25 类型:中考模拟
一、单选题
-
1. 的绝对值是( )A、 B、 C、4 D、2. 经科学家研究,冠状病毒多数为球形或近似球形,其直径约为 米,若用科学记数法表示正确的结果是( ).A、 米 B、 米 C、 米 D、 米3. 如图,几何体由5个相同的小正方体构成,该几何体三视图中为轴对称图形的是( )
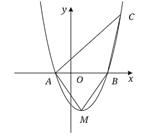
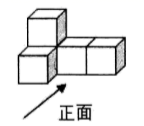 A、主视图 B、左视图 C、视图 D、主视图和俯视图4. 如图,在平面直角坐标系中,△ABC的顶点都在格点上,如果将△ABC先沿y轴翻折,再向上平移3个单位长度,得到 ',那么点B的对应点B'的坐标为( )
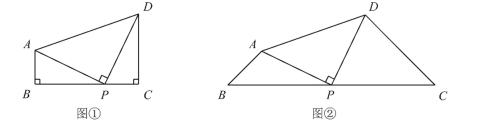
A、主视图 B、左视图 C、视图 D、主视图和俯视图4. 如图,在平面直角坐标系中,△ABC的顶点都在格点上,如果将△ABC先沿y轴翻折,再向上平移3个单位长度,得到 ',那么点B的对应点B'的坐标为( )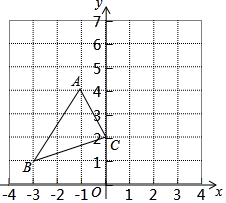 A、(1,7) B、(0,5) C、(3,4) D、(﹣3,2)5. 下列运算正确的是( )A、 B、 C、 D、6. 有一题目:“已知;点 为 的外心, ,求 .”嘉嘉的解答为:画 以及它的外接圆 ,连接 , ,如图.由 ,得 .而淇淇说:“嘉嘉考虑的不周全, 还应有另一个不同的值.”,下列判断正确的是( )
A、(1,7) B、(0,5) C、(3,4) D、(﹣3,2)5. 下列运算正确的是( )A、 B、 C、 D、6. 有一题目:“已知;点 为 的外心, ,求 .”嘉嘉的解答为:画 以及它的外接圆 ,连接 , ,如图.由 ,得 .而淇淇说:“嘉嘉考虑的不周全, 还应有另一个不同的值.”,下列判断正确的是( )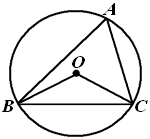 A、淇淇说的对,且 的另一个值是115° B、淇淇说的不对, 就得65° C、嘉嘉求的结果不对, 应得50° D、两人都不对, 应有3个不同值7. 如图,点E是 的边 上的一点,且 ,连接 并延长交 的延长线于点F,若 ,则 的周长为( )
A、淇淇说的对,且 的另一个值是115° B、淇淇说的不对, 就得65° C、嘉嘉求的结果不对, 应得50° D、两人都不对, 应有3个不同值7. 如图,点E是 的边 上的一点,且 ,连接 并延长交 的延长线于点F,若 ,则 的周长为( )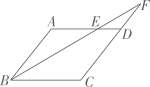 A、21 B、28 C、34 D、428. 对称轴为直线 的抛物线 (a、b、c为常数,且 )如图所示,小明同学得出了以下结论∶① ,② ,③ ,④ ,⑤ (m为任意实数),⑥当 时,y随x的增大而增大.其中结论正确的个数为( )
A、21 B、28 C、34 D、428. 对称轴为直线 的抛物线 (a、b、c为常数,且 )如图所示,小明同学得出了以下结论∶① ,② ,③ ,④ ,⑤ (m为任意实数),⑥当 时,y随x的增大而增大.其中结论正确的个数为( )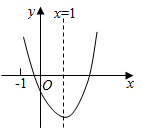 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
9. 若 ,则 的值是 .10. 将含30°角的一个直角三角板和一把直尺(两边a b)如图放置,若∠1=50°,则∠2的度数为 .
 11. 疫情当前,根据上级要求学生在校期间每天都要检测体温,小红连续5天的体温数据如下(单位,℃):36.6,36.2,36.5,36.2,36.3那么这组体温的众数是12. 如图,点C在线段 上,且 ,分别以 、 为边在线段 的同侧作正方形 、 ,连接 、 ,则 .
11. 疫情当前,根据上级要求学生在校期间每天都要检测体温,小红连续5天的体温数据如下(单位,℃):36.6,36.2,36.5,36.2,36.3那么这组体温的众数是12. 如图,点C在线段 上,且 ,分别以 、 为边在线段 的同侧作正方形 、 ,连接 、 ,则 . 13. 如图,点A是反比例函数 图象上的一点, 垂直于x轴,垂足为B. 的面积为6.若点 也在此函数的图象上,则 .
13. 如图,点A是反比例函数 图象上的一点, 垂直于x轴,垂足为B. 的面积为6.若点 也在此函数的图象上,则 .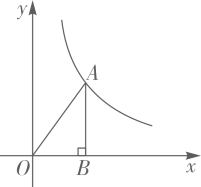 14. 如图, ,在 上截取 .过点 作 ,交 于点 ,以点 为圆心, 为半径画弧,交 于点 ;过点 作 ,交 于点 ,以点 为圆心, 为半径画弧,交 于点 ;按此规律,所得线段 的长等于.
14. 如图, ,在 上截取 .过点 作 ,交 于点 ,以点 为圆心, 为半径画弧,交 于点 ;过点 作 ,交 于点 ,以点 为圆心, 为半径画弧,交 于点 ;按此规律,所得线段 的长等于.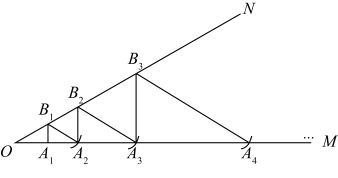
三、解答题
-
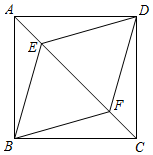
15. 计算: .16. 先化简,再求值:(1+ )÷ ,其中x是不等式组 的整数解.17. 如图,在正方形ABCD中,点E,F在AC上,且AF=CE.求证:四边形BEDF是菱形.
 18. 我县地处黄河半包围之中,周末小亮在爸爸带领下去黄河边游玩.他打算利用自己所学知识测一下某处河水的宽度.如图,他看到河对岸有一棵树A , 于是又在河边取两点B , C , 测得 ,量得 长为 求此处河水的宽度,( 取1.414, 取1.732,结果精确到 ,假定河两岸是平行的).
18. 我县地处黄河半包围之中,周末小亮在爸爸带领下去黄河边游玩.他打算利用自己所学知识测一下某处河水的宽度.如图,他看到河对岸有一棵树A , 于是又在河边取两点B , C , 测得 ,量得 长为 求此处河水的宽度,( 取1.414, 取1.732,结果精确到 ,假定河两岸是平行的).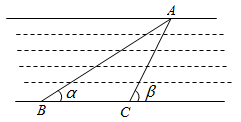 19. 某水果商店销售一种进价为40元/千克的优质水果,若售价为50元/千克,则一个月可售出500千克;若售价在50元/千克的基础上每涨价1元,则月销售量就减少10千克.(1)、当售价为55元/千克时,每月销售水果多少千克?(2)、当月利润为8750元时,每千克水果售价为多少元?(3)、当每千克水果售价为多少元时,获得的月利润最大?20. 在4月23日“世界读书日”来临之际,某校为了了解学生的课外阅读情况,从全校随机抽取了部分学生,调查了他们平均每周的课外阅读时间t(单位:小时).把调查结果分为四档,A档: ;B档: ;C档: ;D档: .根据调查情况,给出了部分数据信息:
19. 某水果商店销售一种进价为40元/千克的优质水果,若售价为50元/千克,则一个月可售出500千克;若售价在50元/千克的基础上每涨价1元,则月销售量就减少10千克.(1)、当售价为55元/千克时,每月销售水果多少千克?(2)、当月利润为8750元时,每千克水果售价为多少元?(3)、当每千克水果售价为多少元时,获得的月利润最大?20. 在4月23日“世界读书日”来临之际,某校为了了解学生的课外阅读情况,从全校随机抽取了部分学生,调查了他们平均每周的课外阅读时间t(单位:小时).把调查结果分为四档,A档: ;B档: ;C档: ;D档: .根据调查情况,给出了部分数据信息:①A档和D档的所有数据是:7,7,7.5,10,7,10,7,7.5,7,7,10.5,10.5;
②图1和图2是两幅不完整的统计图.
根据以上信息解答问题:
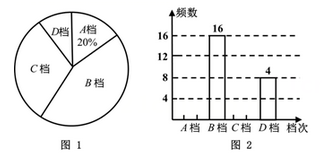 (1)、求本次调查的学生人数,并将图2补充完整;(2)、已知全校共1200名学生,请你估计全校B档的人数;(3)、学校要从D档的4名学生中随机抽取2名作读书经验分享,已知这4名学生1名来自七年级,1名来自八年级,2名来自九年级,请用列表或画树状图的方法,求抽到的2名学生来自不同年级的概率.21. 如图,正比例函数 的图像与反比例函数 的图像交于点 .点B为x轴正半轴上一点,过B作x轴的垂线交反比例函数的图象于点C,交正比例函数的图象于点D.
(1)、求本次调查的学生人数,并将图2补充完整;(2)、已知全校共1200名学生,请你估计全校B档的人数;(3)、学校要从D档的4名学生中随机抽取2名作读书经验分享,已知这4名学生1名来自七年级,1名来自八年级,2名来自九年级,请用列表或画树状图的方法,求抽到的2名学生来自不同年级的概率.21. 如图,正比例函数 的图像与反比例函数 的图像交于点 .点B为x轴正半轴上一点,过B作x轴的垂线交反比例函数的图象于点C,交正比例函数的图象于点D.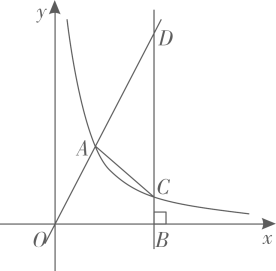 (1)、求a的值及正比例函数 的表达式;(2)、若 ,求 的面积.22. 如图,AB为⊙O的直径,点C是⊙O上一点,CD与⊙O相切于点C,过点A作AD⊥DC,连接AC,BC.
(1)、求a的值及正比例函数 的表达式;(2)、若 ,求 的面积.22. 如图,AB为⊙O的直径,点C是⊙O上一点,CD与⊙O相切于点C,过点A作AD⊥DC,连接AC,BC.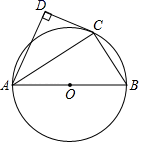 (1)、求证:AC是∠DAB的角平分线;(2)、若AD=2,AB=3,求AC的长.
(1)、求证:AC是∠DAB的角平分线;(2)、若AD=2,AB=3,求AC的长.