山东省菏泽市曹县2021年中考数学一模试卷
试卷更新日期:2021-06-25 类型:中考模拟
一、单选题
-
1. 下列各数中,比﹣2小的数是( )A、﹣1 B、﹣3 C、0 D、2. 下列运算正确的是( ).A、 B、 C、 D、3. 如下摆放的几何体中,主视图与左视图有可能不同的是( )A、
 B、
B、 C、
C、 D、
D、 4. 若不等式 的解集中x的每一个值,都能使关于x的不等式 成立,则m的取值范围是( ).A、 B、 C、 D、5. 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=2cm,将Rt△ABC绕点A逆时针旋转得到Rt△AB'C',使点C'落在AB上,连接BB',则BB'的长为( )
4. 若不等式 的解集中x的每一个值,都能使关于x的不等式 成立,则m的取值范围是( ).A、 B、 C、 D、5. 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=2cm,将Rt△ABC绕点A逆时针旋转得到Rt△AB'C',使点C'落在AB上,连接BB',则BB'的长为( )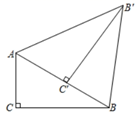 A、2cm B、4cm C、2 cm D、4 cm6. 某班从甲、乙、丙、丁四位选中随机选取两人参加校乒乓球比赛,恰好选中甲、乙两位选手的概率是( )A、 B、 C、 D、7. 如图,正方形 中,点 、 分别在边 , 上, 与 交于点 .若 , ,则 的长为( )
A、2cm B、4cm C、2 cm D、4 cm6. 某班从甲、乙、丙、丁四位选中随机选取两人参加校乒乓球比赛,恰好选中甲、乙两位选手的概率是( )A、 B、 C、 D、7. 如图,正方形 中,点 、 分别在边 , 上, 与 交于点 .若 , ,则 的长为( )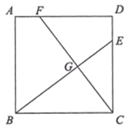 A、 B、 C、 D、8. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,下列结论:(1)b<0,(2)3a+c>0,(3)a+b≤am2+bm(m为任意实数),其中结论正确的个数为( )
A、 B、 C、 D、8. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,下列结论:(1)b<0,(2)3a+c>0,(3)a+b≤am2+bm(m为任意实数),其中结论正确的个数为( ) A、0个 B、1个 C、2个 D、3个
A、0个 B、1个 C、2个 D、3个二、填空题
-
9. 分解因式:x2(x﹣3)﹣x+3=.10. 将含30°角的一个直角三角板和一把直尺(两边a b)如图放置,若∠1=50°,则∠2的度数为 .
 11. 关于x的一元二次方程x2+(k﹣3)x+1﹣k=0的根的情况是 .12. 如图,ABCD是平行四边形,AB是⊙O的直径,点D在⊙O上,AD=OA=2,则图中阴影部分的面积为 .
11. 关于x的一元二次方程x2+(k﹣3)x+1﹣k=0的根的情况是 .12. 如图,ABCD是平行四边形,AB是⊙O的直径,点D在⊙O上,AD=OA=2,则图中阴影部分的面积为 . 13. 如图,在平面直角坐标系中,点A , B的坐标分别为(﹣ ,0),( ,1),连接AB , 以AB为边作等边△ABC , 则点C的坐标为 .
13. 如图,在平面直角坐标系中,点A , B的坐标分别为(﹣ ,0),( ,1),连接AB , 以AB为边作等边△ABC , 则点C的坐标为 . 14. 如图,折叠矩形纸片 ,使点D落在 边的点M处,点C落在点N处, 为折痕, , ,设 ,四边形 的面积为S,则S关于t的函数表达式为 .
14. 如图,折叠矩形纸片 ,使点D落在 边的点M处,点C落在点N处, 为折痕, , ,设 ,四边形 的面积为S,则S关于t的函数表达式为 .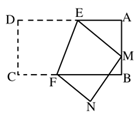
三、解答题
-
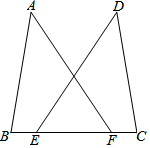
15. 计算:( )﹣1+ sin60°﹣|﹣ |﹣( ﹣3)0 .16. 先化简,再求值:( ﹣x)÷ ,其中x=﹣1 .17. 如图,点 , 在 上, , , ,求证: .
 18. 如图,为测量楼CD的高度,从楼AB的顶点A测得楼CD的顶部点D的仰角为45°,底部C的俯角为30°,已知楼AB的高为30米,求楼CD的高度.
18. 如图,为测量楼CD的高度,从楼AB的顶点A测得楼CD的顶部点D的仰角为45°,底部C的俯角为30°,已知楼AB的高为30米,求楼CD的高度.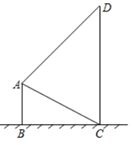 19. 某中学为了解学生学习校本课程《文明礼仪》的情况,随机抽取了20名学生的测试成绩,经过整理,得到了频数分布表和扇形统计图.
19. 某中学为了解学生学习校本课程《文明礼仪》的情况,随机抽取了20名学生的测试成绩,经过整理,得到了频数分布表和扇形统计图.等级
成绩/分
频数
A
95≤x≤100
a
B
90≤x<95
8
C
85≤x<90
5
D
80≤x<85
4
 (1)、求a , b的值;(2)、若成绩不低于90分为优秀,估计该校1200名学生中,达到优秀等级的人数.20. 如图,一次函数y=kx+b的图象与反比例函数y= 的图象在第一象限内交于点A , 与x轴交于点B(5,0),若OB=AB , 且S△OAB= ,求反比例函数与一次函数的表达式.
(1)、求a , b的值;(2)、若成绩不低于90分为优秀,估计该校1200名学生中,达到优秀等级的人数.20. 如图,一次函数y=kx+b的图象与反比例函数y= 的图象在第一象限内交于点A , 与x轴交于点B(5,0),若OB=AB , 且S△OAB= ,求反比例函数与一次函数的表达式.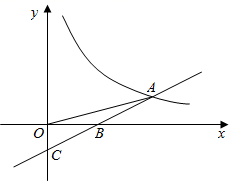 21. 某社区购买甲、乙两种树苗进行绿化,已知甲种树苗每棵30元,乙种树苗每棵20元,且乙种树苗棵数比甲种树苗棵数的2倍少40棵,购买两种树苗的总金额为9000元.(1)、求购买甲、乙两种树苗各多少棵?(2)、为保证绿化效果,社区决定再购买甲、乙两种树苗共10棵,总费用不超过230元,求可能的购买方案?22. 如图, 中, ,点D为 上一点,以 为直径的 交 于点E,连接 , 平分 .
21. 某社区购买甲、乙两种树苗进行绿化,已知甲种树苗每棵30元,乙种树苗每棵20元,且乙种树苗棵数比甲种树苗棵数的2倍少40棵,购买两种树苗的总金额为9000元.(1)、求购买甲、乙两种树苗各多少棵?(2)、为保证绿化效果,社区决定再购买甲、乙两种树苗共10棵,总费用不超过230元,求可能的购买方案?22. 如图, 中, ,点D为 上一点,以 为直径的 交 于点E,连接 , 平分 . (1)、求证: 是 的切线;(2)、若 , ,求 的半径.23. 如图, 由 绕点 按逆时针方向旋转 得到,且点 的对应点D恰好落在 的延长线上, , 相交于点 .
(1)、求证: 是 的切线;(2)、若 , ,求 的半径.23. 如图, 由 绕点 按逆时针方向旋转 得到,且点 的对应点D恰好落在 的延长线上, , 相交于点 . (1)、求 的度数;(2)、 是 延长线上的点,且 .
(1)、求 的度数;(2)、 是 延长线上的点,且 .①判断 和 的数量关系,并证明;
②求证: .
24. 如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C(0,3),顶点为点D . (1)、求抛物线的函数表达式;(2)、若过点C的直线交线段AB于点E , 且S△ACE:S△CEB=3:5,求直线CE的函数表达式;(3)、若点P在抛物线上,点Q在x轴上,是否存在以点D , C , P , Q为顶点的四边形是平行四边形,若存在,求出点P的坐标,若不存在,请说明理由.
(1)、求抛物线的函数表达式;(2)、若过点C的直线交线段AB于点E , 且S△ACE:S△CEB=3:5,求直线CE的函数表达式;(3)、若点P在抛物线上,点Q在x轴上,是否存在以点D , C , P , Q为顶点的四边形是平行四边形,若存在,求出点P的坐标,若不存在,请说明理由.