山东省东营市东营区2021年中考数学二模试卷
试卷更新日期:2021-06-25 类型:中考模拟
一、单选题
-
1. 下列各数中,绝对值最小的数是( )A、 B、 C、 D、2. 下列垃圾分类标识的图案既是轴对称图形,又是中心对称图形的是( )A、
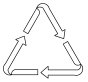 B、
B、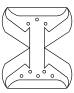 C、
C、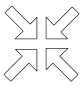 D、
D、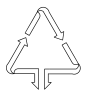 3. 下列计算正确的是( )A、 B、 C、 D、4. 有20张背面完全一样的卡片,其中8张正面印有天鹅湖风光,7张正面印有黄河入海口自然风景,5张正面印有孙武湖景色.把这些卡片的背面朝上,搅匀后从中随机抽出一张卡片,抽到正面是天鹅湖风光卡片的概率是( )A、 B、 C、 D、5. 不等式组 的解集在数轴上表示正确的是( )A、
3. 下列计算正确的是( )A、 B、 C、 D、4. 有20张背面完全一样的卡片,其中8张正面印有天鹅湖风光,7张正面印有黄河入海口自然风景,5张正面印有孙武湖景色.把这些卡片的背面朝上,搅匀后从中随机抽出一张卡片,抽到正面是天鹅湖风光卡片的概率是( )A、 B、 C、 D、5. 不等式组 的解集在数轴上表示正确的是( )A、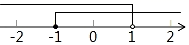 B、
B、 C、
C、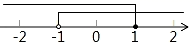 D、
D、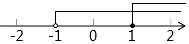 6. 如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作与△OAB的位似比为 的位似图形△OCD,则点C坐标( )
6. 如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作与△OAB的位似比为 的位似图形△OCD,则点C坐标( )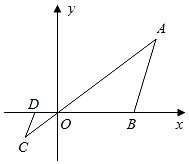 A、(﹣1,﹣1) B、(﹣ ,﹣1) C、(﹣1,﹣ ) D、(﹣2,﹣1)7. 如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的大小为( )
A、(﹣1,﹣1) B、(﹣ ,﹣1) C、(﹣1,﹣ ) D、(﹣2,﹣1)7. 如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的大小为( )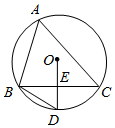 A、55° B、65° C、60° D、75°8. 如图,在矩形ABCD中,AB=3,BC=4,动点P沿折线BCD从点B开始运动到点D,设点P运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是( )
A、55° B、65° C、60° D、75°8. 如图,在矩形ABCD中,AB=3,BC=4,动点P沿折线BCD从点B开始运动到点D,设点P运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是( )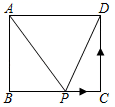 A、
A、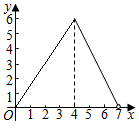 B、
B、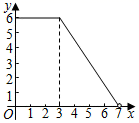 C、
C、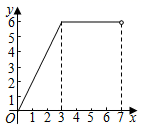 D、
D、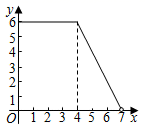 9. 如图,把一张矩形纸片ABCD按所示方法进行两次折叠,得到等腰直角三角形BEF,若BC=1,则AB的长度为( )
9. 如图,把一张矩形纸片ABCD按所示方法进行两次折叠,得到等腰直角三角形BEF,若BC=1,则AB的长度为( ) A、 B、 C、 D、10. 如图,在正方形ABCD中,连接AC , 以点A为圆心,适当长为半径画弧,交AB、AC于点M , N , 分别以M , N为圆心,大于MN长的一半为半径画弧,两弧交于点H , 连结AH并延长交BC于点E , 再分别以A、E为圆心,以大于AE长的一半为半径画弧,两弧交于点P , Q , 作直线PQ , 分别交CD , AC , AB于点F , G , L , 交CB的延长线于点K , 连接GE , 下列结论:
A、 B、 C、 D、10. 如图,在正方形ABCD中,连接AC , 以点A为圆心,适当长为半径画弧,交AB、AC于点M , N , 分别以M , N为圆心,大于MN长的一半为半径画弧,两弧交于点H , 连结AH并延长交BC于点E , 再分别以A、E为圆心,以大于AE长的一半为半径画弧,两弧交于点P , Q , 作直线PQ , 分别交CD , AC , AB于点F , G , L , 交CB的延长线于点K , 连接GE , 下列结论:
① ;② ; ③ ; ④ .其中正确的是( )
A、①②③ B、②③④ C、①③④ D、①②④二、填空题
-
11. 有一种病毒的直径大约是0.00000068米,则它的直径用科学记数法可表示为米.12. 分解因式: = .13. 已知:直线l1∥l2 , 将一块含30°角的直角三角板如图所示放置,若∠1=25°,则∠2=度.
 14. 在党中央的正确领导和全国人民的共同努力下,我国新冠肺炎确诊人数逐日下降,同时为构建人类命运共同体,我国积极派出医疗队帮助其他国家抗疫,由我国援助的Y国刚开始每周新增新冠肺炎确诊人数是2500人,两周后每周新增新冠肺炎确诊人数是1600人,若平均每周下降的百分率相同,则平均每周下降的百分率是 .15. 某学习小组在“世界读书日”这天统计了本组5名同学在上学期阅读课外书籍的册数,数据是18,x,15,16,13,若这组数据的平均数为16,则这组数据的中位数是 .16. 2022年在北京将举办第24届冬季奥运会,很多学校都开展了冰雪项目学习.如图,滑雪轨道由AB、BC两部分组成,AB、BC的长度都为200米,一位同学乘滑雪板沿此轨道由A点滑到了C点,若AB与水平面的夹角α为20°,BC与水平面的夹角β为45°,则他下降的高度为米(精确到1米, ,sin20o=0.3420,tan20o=0.3640,cos20o=0.9400).
14. 在党中央的正确领导和全国人民的共同努力下,我国新冠肺炎确诊人数逐日下降,同时为构建人类命运共同体,我国积极派出医疗队帮助其他国家抗疫,由我国援助的Y国刚开始每周新增新冠肺炎确诊人数是2500人,两周后每周新增新冠肺炎确诊人数是1600人,若平均每周下降的百分率相同,则平均每周下降的百分率是 .15. 某学习小组在“世界读书日”这天统计了本组5名同学在上学期阅读课外书籍的册数,数据是18,x,15,16,13,若这组数据的平均数为16,则这组数据的中位数是 .16. 2022年在北京将举办第24届冬季奥运会,很多学校都开展了冰雪项目学习.如图,滑雪轨道由AB、BC两部分组成,AB、BC的长度都为200米,一位同学乘滑雪板沿此轨道由A点滑到了C点,若AB与水平面的夹角α为20°,BC与水平面的夹角β为45°,则他下降的高度为米(精确到1米, ,sin20o=0.3420,tan20o=0.3640,cos20o=0.9400). 17. 在平面直角坐标系中,点A的坐标为 ,点B的坐标为 ,点C、D分别为坐标轴x轴和y轴上的任意一点,则四边形 的周长的最小值为 .18. 如图,在平面直角坐标系中,直线l的函数表达式为 ,点 的坐标为 以 为圆心, 为半径画圆,交直线l于点P,交 轴正半轴于点 ;以 为圆心, 为半径画圆,交直线l于点 ,交x轴正半轴于点 ;以 为圆心, 为半径画圆,交直线l于点 ,交x轴正半轴于点 ;······按此做法进行下去,其中弧 的长 .
17. 在平面直角坐标系中,点A的坐标为 ,点B的坐标为 ,点C、D分别为坐标轴x轴和y轴上的任意一点,则四边形 的周长的最小值为 .18. 如图,在平面直角坐标系中,直线l的函数表达式为 ,点 的坐标为 以 为圆心, 为半径画圆,交直线l于点P,交 轴正半轴于点 ;以 为圆心, 为半径画圆,交直线l于点 ,交x轴正半轴于点 ;以 为圆心, 为半径画圆,交直线l于点 ,交x轴正半轴于点 ;······按此做法进行下去,其中弧 的长 .
三、解答题
-
19.(1)、计算(2)、化简式子 并在0,2,3中选取一个合适的数作为x的值代入求值.20. 《中国汉字听写大会》唤醒了很多人对文字基本功的重视和对汉字文化的学习,我区某校组织了一次全校2000名学生参加的“汉字听写大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表:
抽取的200名学生海选成绩分组表
组别
海选成绩
A组
B组
C组
D组
E组
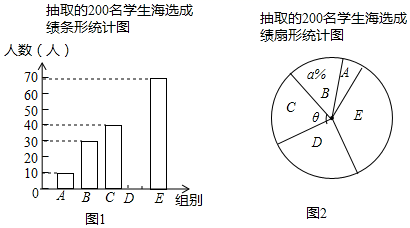
请根据所给信息,解答下列问题:
(1)、求出D组的人数,并把图1中的条形统计图补充完整;(请画在答题卷相对应的图上)(2)、在图2的扇形统计图中,记表示B组人数所占的百分比为 ,则a的值为 , 表示C组扇形的圆心角 的度数为度;(3)、规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?(4)、经过统计发现,在E组中,有2位男生和2位女生获得了满分,如果从这4人中挑选2人代表学校参加比赛,请用树状图或列表法求出所选两人正好是一男一女的概率是多少?21. 如图,在 中,D是边 上一点,以 为直径的 经过点A,且 . (1)、请判断直线 是否是 的切线,并说明理由;(2)、若 , ,求半径的长.22. 如图,已知一次函数 与反比例函数 的图象在第一、三象限分别交于 , 两点,连接 , .
(1)、请判断直线 是否是 的切线,并说明理由;(2)、若 , ,求半径的长.22. 如图,已知一次函数 与反比例函数 的图象在第一、三象限分别交于 , 两点,连接 , .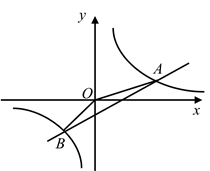 (1)、求一次函数和反比例函数的解析式;(2)、 的面积为;(3)、直接写出 时x的取值范围.23. 一方有难,八方支援.2020年初,新冠肺炎爆发,山东某蔬菜基地运输公司计划安排甲、乙两种货车向某疫区运送新鲜蔬菜,两次满载的运输情况如下表:
(1)、求一次函数和反比例函数的解析式;(2)、 的面积为;(3)、直接写出 时x的取值范围.23. 一方有难,八方支援.2020年初,新冠肺炎爆发,山东某蔬菜基地运输公司计划安排甲、乙两种货车向某疫区运送新鲜蔬菜,两次满载的运输情况如下表:次数
甲种货车辆数
乙种货车辆数
合计运送吨数
第一次
2
3
19
第二次
3
5
30
(1)、求甲、乙两种货车每次满载分别能运输多少吨新鲜蔬菜?(2)、目前至少有36吨新鲜蔬菜要一次性运输到目的地,该公司拟安排甲、乙两种货车共8辆,其中每辆甲种货车一次运送费用为500元,每辆乙种货车一次运送费用为300元,请问该公司应如何安排甲、乙两种货车使总运送费用最少?24. 如图1 ,在 中, 是 边上一点(不与点 重合),将线段 绕点A逆时针旋转 得到 ,连接 .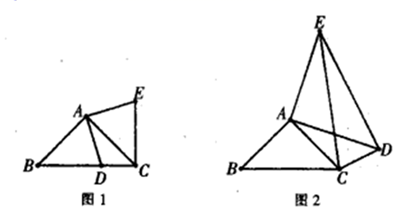 (1)、(发现问题)
(1)、(发现问题)如图1 ,通过图形旋转的性质,可知 , 度;
(2)、(解决问题)如图1,证明 ;
(3)、(拓展延伸)如图2,在 中, 为 外一点,且 ,仍将线段 绕点A逆时针旋转 得到 ,连接 .
若 求的 长.
25. 如图,在平面直角坐标系中,已知点C(0,4),点A、B在x轴上,并且OA=OC=4OB , 动点P在过A、B、C三点的抛物线上.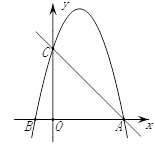
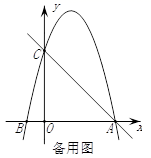 (1)、求抛物线的函数表达式;(2)、在直线AC上方的抛物线上,是否存在点P , 使得△PAC的面积最大?若存在,求出P点坐标及ΔPAC面积的最大值;若不存在,请说明理由.(3)、在x轴上是否存在点Q , 使得△ACQ是等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
(1)、求抛物线的函数表达式;(2)、在直线AC上方的抛物线上,是否存在点P , 使得△PAC的面积最大?若存在,求出P点坐标及ΔPAC面积的最大值;若不存在,请说明理由.(3)、在x轴上是否存在点Q , 使得△ACQ是等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.