山东省德州市禹城市、临邑县2021年中考数学二模试卷
试卷更新日期:2021-06-25 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 如图是由4个完全相同的正方形搭成的几何体,则( )
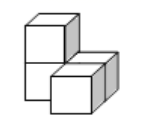 A、三视图都相同 B、俯视图与左视图都相同 C、主视图与俯视图都相同 D、主视图与左视图相同3. 2019新型冠状病毒的直径是 ,将0.00012用科学记数法表示是( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE与AD相交于点F , ∠EDF=42°,则∠DBE的度数是( )
A、三视图都相同 B、俯视图与左视图都相同 C、主视图与俯视图都相同 D、主视图与左视图相同3. 2019新型冠状病毒的直径是 ,将0.00012用科学记数法表示是( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE与AD相交于点F , ∠EDF=42°,则∠DBE的度数是( )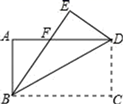 A、21° B、23° C、24° D、42°6. 定义运算: .例如 .则方程 的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、只有一个实数根7. 在一次选美比赛中,某选手的得分如下:92,89,96,94,90,96,98,96.这组数据的众数和中位数分别是( )A、96,95 B、96,96 C、95,95 D、95,948. 如图,在 中, ,以点C为圆心, 长为半径画弧,交 于点B和点D , 再分别以点B , D为圆心,大于 长为半径画弧,两弧相交于点M , 作射线 交 于点E . 若 ,则 的长度是( )
A、21° B、23° C、24° D、42°6. 定义运算: .例如 .则方程 的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、只有一个实数根7. 在一次选美比赛中,某选手的得分如下:92,89,96,94,90,96,98,96.这组数据的众数和中位数分别是( )A、96,95 B、96,96 C、95,95 D、95,948. 如图,在 中, ,以点C为圆心, 长为半径画弧,交 于点B和点D , 再分别以点B , D为圆心,大于 长为半径画弧,两弧相交于点M , 作射线 交 于点E . 若 ,则 的长度是( )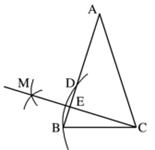 A、 B、 C、9 D、9. 如图,PA是⊙O的切线,切点为A,PO的延长线交⊙O于点B,若∠P=40°,则∠B的度数为( )
A、 B、 C、9 D、9. 如图,PA是⊙O的切线,切点为A,PO的延长线交⊙O于点B,若∠P=40°,则∠B的度数为( )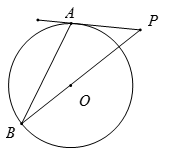 A、20° B、25° C、40° D、50°10. 二次函数y=ax2+bx+c的图象如下左图所示,则一次函数y=ax+b和反比例函数y 在同一平面直角坐标系中的图象可能是( )
A、20° B、25° C、40° D、50°10. 二次函数y=ax2+bx+c的图象如下左图所示,则一次函数y=ax+b和反比例函数y 在同一平面直角坐标系中的图象可能是( ) A、
A、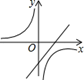 B、
B、 C、
C、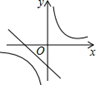 D、
D、 11. 如图所示,矩形纸片 中, ,把它分割成正方形纸片 和矩形纸片 后,分别裁出扇形 和半径最大的圆,恰好能作为一个圆锥的底面和侧面,则圆锥的表面积为( )
11. 如图所示,矩形纸片 中, ,把它分割成正方形纸片 和矩形纸片 后,分别裁出扇形 和半径最大的圆,恰好能作为一个圆锥的底面和侧面,则圆锥的表面积为( )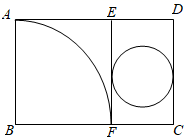 A、 B、 C、 D、12. 在平面直角坐标系中,正方形 的位置如图所示,点A的坐标为 ,点D的坐标为 ,延长 交x轴于点 ,作正方形 ;延长 交x轴于点 ,作正方形 …按这样的规律进行下去,正方形 的面积为( )
A、 B、 C、 D、12. 在平面直角坐标系中,正方形 的位置如图所示,点A的坐标为 ,点D的坐标为 ,延长 交x轴于点 ,作正方形 ;延长 交x轴于点 ,作正方形 …按这样的规律进行下去,正方形 的面积为( )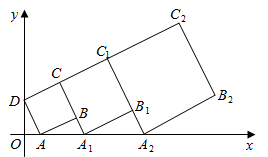 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
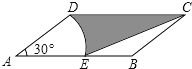
13. 若代数式 有意义,则x的取值范围是.14. 如图,在▱ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是 (结果保留π).
 15. 已知电路AB由如图所示的开关控制,闭合a,b,c,d,e五个开关中的任意两个,则使电路形成通路的概率是.
15. 已知电路AB由如图所示的开关控制,闭合a,b,c,d,e五个开关中的任意两个,则使电路形成通路的概率是. 16. 若关于x的分式方程 的解为正数,则m的取值范围为 .17. 如图,菱形 的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是5和8,反比例函数 的图象经过点C , 则k的值为 .
16. 若关于x的分式方程 的解为正数,则m的取值范围为 .17. 如图,菱形 的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是5和8,反比例函数 的图象经过点C , 则k的值为 .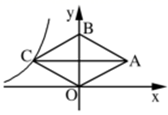 18. 如图,点O为正方形 的中心, 平分 交 于点E , 延长 到点F , 使 ,连接 交 的延长线于点H , 连接 交 于点G , 连接 .则以下五个结论中① ;② ;③ ;④ ;⑤ ,正确结论为 .
18. 如图,点O为正方形 的中心, 平分 交 于点E , 延长 到点F , 使 ,连接 交 的延长线于点H , 连接 交 于点G , 连接 .则以下五个结论中① ;② ;③ ;④ ;⑤ ,正确结论为 .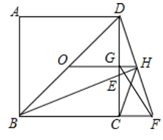
三、解答题
-
19. 先化简,再求值: ,其中x是一元二次方程 的解.20. 为培养学生的阅读习惯,某中学利用学生课外时间开展了以“走近名著”为主题的读书活动.为了有效了解学生课外阅读情况,现随机调查了部分学生每周课外阅读的时间,设被调查的每名学生每周课外阅读的总时间为 小时,将它分为4个等级:A( ),B( ),C( ),D( ),并根据调查结果绘制了如两幅不完整的统计图:
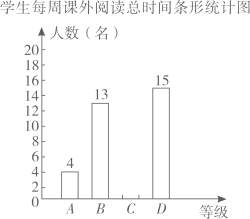
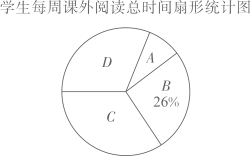
请你根据统计图的信息,解决下列问题:
(1)、本次共调查了名学生;(2)、在扇形统计图中,等级 所对应的扇形的圆心角为°;(3)、请补全条形统计图;(4)、在等级D中有甲、乙、丙、丁4人表现最为优秀,现从4人中任选2人作为学校本次读书活动的宣传员,用列表或画树状图的方法求恰好选中甲和乙的概率.21. 某工厂计划在每个生产周期内生产并销售完某型设备,设备的生产成本为10万元/件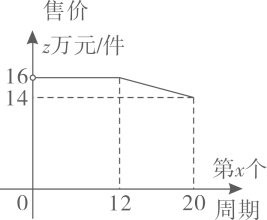 (1)、如图,设第x(0<x≤20)个生产周期设备售价z万元/件,z与x之间的关系用图中的函数图象表示,求z关于x的函数解析式(写出x的范围).(2)、设第x个生产周期生产并销售的设备为y件,y与x满足关系式y=5x+40(0<x≤20).在(1)的条件下,工厂在第几个生产周期创造的利润最大?最大为多少万元?(利润=收入-成本)22. 在数学实践与综合课上,某兴趣小组同学用航拍无人机对某居民小区的1、2号楼进行测高实践,如图为实践时绘制的截面图.无人机从地面点B垂直起飞到达点A处,测得1号楼顶部E的俯角为67°,测得2号楼顶部F的俯角为40°,此时航拍无人机的高度为60米,已知1号楼的高度为20米,且EC和FD分别垂直地面于点C和D , 点B为CD的中点,求2号楼的高度.(结果精确到0.1)(参考数据sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin67°≈0.92,cos67°≈0.39,tan67°≈2.36)
(1)、如图,设第x(0<x≤20)个生产周期设备售价z万元/件,z与x之间的关系用图中的函数图象表示,求z关于x的函数解析式(写出x的范围).(2)、设第x个生产周期生产并销售的设备为y件,y与x满足关系式y=5x+40(0<x≤20).在(1)的条件下,工厂在第几个生产周期创造的利润最大?最大为多少万元?(利润=收入-成本)22. 在数学实践与综合课上,某兴趣小组同学用航拍无人机对某居民小区的1、2号楼进行测高实践,如图为实践时绘制的截面图.无人机从地面点B垂直起飞到达点A处,测得1号楼顶部E的俯角为67°,测得2号楼顶部F的俯角为40°,此时航拍无人机的高度为60米,已知1号楼的高度为20米,且EC和FD分别垂直地面于点C和D , 点B为CD的中点,求2号楼的高度.(结果精确到0.1)(参考数据sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin67°≈0.92,cos67°≈0.39,tan67°≈2.36)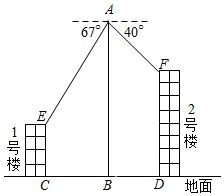 23. 如图,△ABC是⊙O的内接三角形,∠BAC=75°,∠ABC=45°.连接AO并延长,交⊙O于点D,连接BD.过点C作⊙O的切线,与BA的延长线相交于点E.
23. 如图,△ABC是⊙O的内接三角形,∠BAC=75°,∠ABC=45°.连接AO并延长,交⊙O于点D,连接BD.过点C作⊙O的切线,与BA的延长线相交于点E. (1)、求证:AD∥EC;(2)、若AB=12,求线段EC的长.24. 阅读下面的材料:按照一定顺序排列着的一列数称为数列,数列中的每一个数叫做这个数列的项.排在第一位的数称为第一项,记为 ,排在第二位的数称为第二项,记为 ,依次类推,排在第n位的数称为第n项,记为 .所以,数列的一般形式可以写成: .
(1)、求证:AD∥EC;(2)、若AB=12,求线段EC的长.24. 阅读下面的材料:按照一定顺序排列着的一列数称为数列,数列中的每一个数叫做这个数列的项.排在第一位的数称为第一项,记为 ,排在第二位的数称为第二项,记为 ,依次类推,排在第n位的数称为第n项,记为 .所以,数列的一般形式可以写成: .一般地,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,那么这个数列叫做等差数列,这个常数叫做等差数列的公差,公差通常用d表示.如:数列1,3,5,7,…为等差数列,其中 ,公差为 .
根据以上材料,解答下列问题:
(1)、等差数列5,10,15,…的公差d为 , 第5项是 .(2)、如果一个数列 ,是等差数列,且公差为d , 那么根据定义可得到:.
所以
,
,
,
……
由此,请你填空完成等差数列的通项公式:an=a1+()d .
(3)、 是不是等差数列 的项?如果是,是第几项?(4)、如果一个数列 是等差数列,且公差为d , 前n项的和记为 ,请用含 ,n , d的代数式表示 , .25. 二次函数 的图象交x轴于 两点,交y轴于点C.动点M从点A出发,以每秒2个单位长度的速度沿 方向运动,过点M作 轴交直线 于点N,交抛物线于点D,连接 .设运动的时间为t秒.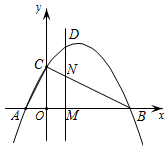 (1)、求二次函数 的表达式:(2)、连接 ,当 时,求 的面积:(3)、在直线 上存在一点P,当 是以 为直角的等腰直角三角形时,求此时点D的坐标;(4)、当 时,在直线 上存在一点Q,使得 ,求点Q的坐标
(1)、求二次函数 的表达式:(2)、连接 ,当 时,求 的面积:(3)、在直线 上存在一点P,当 是以 为直角的等腰直角三角形时,求此时点D的坐标;(4)、当 时,在直线 上存在一点Q,使得 ,求点Q的坐标