山东省德州市夏津县2021年中考数学一模试卷
试卷更新日期:2021-06-25 类型:中考模拟
一、单选题
-
1. 数1,0, ,﹣2中最大的是( )A、1 B、0 C、 D、﹣22. 下列图形既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 分别观察下列几何体,其中主视图、左视图和俯视图完全相同的是( )A、
3. 分别观察下列几何体,其中主视图、左视图和俯视图完全相同的是( )A、 圆锥
B、
圆锥
B、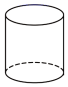 圆柱
C、
圆柱
C、 三棱柱
D、
三棱柱
D、 正方体
4. 下列运算正确的是( )A、a+2a=3a2 B、 C、 D、5. 如图,将直尺与含30°角的三角尺叠放在一起,若∠1=40°,则∠2的大小是( )
正方体
4. 下列运算正确的是( )A、a+2a=3a2 B、 C、 D、5. 如图,将直尺与含30°角的三角尺叠放在一起,若∠1=40°,则∠2的大小是( )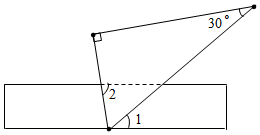 A、40° B、60° C、70° D、80°6. 为调动学生参与体育锻炼的积极性,某校组织了一分钟跳绳比赛活动,体育组随机抽取了10名参赛学生的成绩,将这组数据整理后制成统计表:
A、40° B、60° C、70° D、80°6. 为调动学生参与体育锻炼的积极性,某校组织了一分钟跳绳比赛活动,体育组随机抽取了10名参赛学生的成绩,将这组数据整理后制成统计表:一分钟跳绳个数(个)
141
144
145
146
学生人数(名)
5
2
1
2
则关于这组数据的结论正确的是( )
A、平均数是144 B、众数是141 C、中位数是144.5 D、方差是5.47. 以下说法正确的是( )A、平行四边形的对边相等 B、圆周角等于圆心角的一半 C、同位角相等 D、三角形的一个外角等于两个内角的和8. 如图,在△ABC中,按以下步骤作图:①分别以点B和C为圆心,以大于 BC的长为半径作弧,两弧相交于点M和N ;②作直线MN交AC于点D,连接BD。若AC=6,AD=2,则BD的长为( )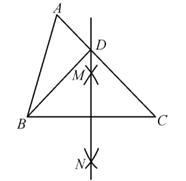 A、2 B、3 C、4 D、69. 如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C、D,则 的值为( )
A、2 B、3 C、4 D、69. 如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C、D,则 的值为( )
 A、 B、 C、 D、10. 如图,半径为10的扇形 中, , 为 上一点, , ,垂足分别为 、 .若 为 ,则图中阴影部分的面积为( )
A、 B、 C、 D、10. 如图,半径为10的扇形 中, , 为 上一点, , ,垂足分别为 、 .若 为 ,则图中阴影部分的面积为( ) A、 B、 C、 D、11. 二次函数 的顶点坐标为 ,其部分图象如图所示.以下结论错误的是( )
A、 B、 C、 D、11. 二次函数 的顶点坐标为 ,其部分图象如图所示.以下结论错误的是( ) A、 B、 C、 D、关于x的方程 无实数根12. 如图,矩形纸片ABCD中,AB=6,BC=12.将纸片折叠,使点B落在边AD的延长线上的点G处,折痕为EF,点E、F分别在边AD和边BC上.连接BG,交CD于点K,FG交CD于点H.给出以下结论:①EF⊥BG;②GE=GF;③△GDK和△GKH的面积相等;④当点F与点C重合时,∠DEF=75°.其中正确的结论共有( )
A、 B、 C、 D、关于x的方程 无实数根12. 如图,矩形纸片ABCD中,AB=6,BC=12.将纸片折叠,使点B落在边AD的延长线上的点G处,折痕为EF,点E、F分别在边AD和边BC上.连接BG,交CD于点K,FG交CD于点H.给出以下结论:①EF⊥BG;②GE=GF;③△GDK和△GKH的面积相等;④当点F与点C重合时,∠DEF=75°.其中正确的结论共有( )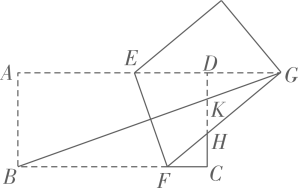 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
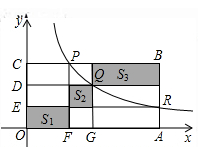
13. 定义a※b=a(b+1),例如2※3=2×(3+1)=2×4=8.则(x﹣1)※x的结果为 .14. 若关于x的分式方程 有增根,则m= .15. 圆锥的底面半径为3,侧面积为 ,则这个圆锥的母线长为.16. 点P,Q,R在反比例函数 (常数k>0,x>0)图象上的位置如图所示,分别过这三个点作x轴、y轴的平行线.图中所构成的阴影部分面积从左到右依次为S1 , S2 , S3.若OE=ED=DC,S1+S3=27,则S2的值为.
 17. 如图,在平面直角坐标系中, , , ,…都是等腰直角三角形,其直角顶点 , , .…均在直线 上.设 , , ,…的面积分别为 , , ,….依据图形所反映的规律,则 .
17. 如图,在平面直角坐标系中, , , ,…都是等腰直角三角形,其直角顶点 , , .…均在直线 上.设 , , ,…的面积分别为 , , ,….依据图形所反映的规律,则 .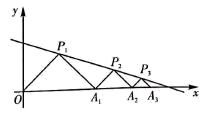
三、解答题
-
18. 先化简,再求值: ,其中 是不等式组 的整数解.19. 某学校为了解全校学生对电视节目的喜爱情况(新闻、体育、动画、娱乐、戏曲),从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.

请根据以上信息,解答下列问题:
(1)、这次被调查的学生共有多少人?
(2)、请将条形统计图补充完整;(3)、若该校约有1500名学生,估计全校学生中喜欢娱乐节目的有多少人?(4)、该校广播站需要广播员,现决定从喜欢新闻节目的甲、乙、丙、丁四名同学中选取2名,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)20. 如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°,点A距地面2.5米,点B距地面10.5米.为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4, ≈1.4) 21. 如图,△ABC内接于⊙O,AB为⊙O的直径,AB=10,AC=6。连结OC,弦AD分别交OC,BC于点E,F,其中点E是AD的中点。
21. 如图,△ABC内接于⊙O,AB为⊙O的直径,AB=10,AC=6。连结OC,弦AD分别交OC,BC于点E,F,其中点E是AD的中点。 (1)、求证:∠CAD=∠CBA。(2)、求OE的长。22. 为了更好治理和净化运河,保护环境,运河综合治理指挥部决定购买10台污水处理设备.现有A、B两种型号的设备,其中每台的价格、月处理污水量如下表.
(1)、求证:∠CAD=∠CBA。(2)、求OE的长。22. 为了更好治理和净化运河,保护环境,运河综合治理指挥部决定购买10台污水处理设备.现有A、B两种型号的设备,其中每台的价格、月处理污水量如下表.A型
B型
价格(万元/台)
a
b
处理污水量(吨/月)
220
180
经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
(1)、求a , b的值;(2)、由于受资金限制,运河综合治理指挥部决定购买污水处理设备的资金不超过110万元,问每月最多能处理污水多少吨?23. 背景:一次小组合作探究课上,小明将两个正方形按背景图位置摆放(点E,A,D在同一条直线上),发现BE=DG且BE⊥DG.小组讨论后,提出了三个问题,请你帮助解答: (1)、将正方形AEFG绕点A按逆时针方向旋转,(如图1)还能得到BE=DG吗?如果能,请给出证明.如若不能,请说明理由:(2)、把背景中的正方形分别改为菱形AEFG和菱形ABCD,将菱形AEFG绕点A按顺时针方向旋转,(如图2)试问当∠EAG与∠BAD的大小满足怎样的关系时,背景中的结论BE=DG仍成立?请说明理由;(3)、把背景中的正方形改成矩形AEFG和矩形ABCD,且 ,AE=4,AB=8,将矩形AEFG绕点A按顺时针方向旋转(如图3),连接DE,BG.小组发现:在旋转过程中, BG2+DE2是定值,请求出这个定值.24. 如图,对称轴为直线x=1的抛物线y=x2﹣bx+c与x轴交于A(x1 , 0)、B(x2 , 0)(x1<x2)两点,与y轴交于C点,且 ﹣ .
(1)、将正方形AEFG绕点A按逆时针方向旋转,(如图1)还能得到BE=DG吗?如果能,请给出证明.如若不能,请说明理由:(2)、把背景中的正方形分别改为菱形AEFG和菱形ABCD,将菱形AEFG绕点A按顺时针方向旋转,(如图2)试问当∠EAG与∠BAD的大小满足怎样的关系时,背景中的结论BE=DG仍成立?请说明理由;(3)、把背景中的正方形改成矩形AEFG和矩形ABCD,且 ,AE=4,AB=8,将矩形AEFG绕点A按顺时针方向旋转(如图3),连接DE,BG.小组发现:在旋转过程中, BG2+DE2是定值,请求出这个定值.24. 如图,对称轴为直线x=1的抛物线y=x2﹣bx+c与x轴交于A(x1 , 0)、B(x2 , 0)(x1<x2)两点,与y轴交于C点,且 ﹣ .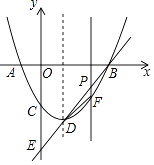 (1)、求抛物线的解析式;(2)、抛物线顶点为D,直线BD交y轴于E点;
(1)、求抛物线的解析式;(2)、抛物线顶点为D,直线BD交y轴于E点;①设点P为线段BD上一点(点P不与B、D两点重合),过点P作x轴的垂线与抛物线交于点F,求△BDF面积的最大值;
②在线段BD上是否存在点Q,使得∠BDC=∠QCE?若存在,求出点Q的坐标;若不存在,请说明理由.