江西省赣州市2021年中考数学模拟试卷

试卷更新日期：2021-06-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算 $| - 6 |$ 的结果等于（）

A、6 B、 $- 6$ C、 $\frac{1}{6}$ D、 $- \frac{1}{6}$

查看试题解析
2. 图中阴影部分是由4个完全相同的正方形拼接而成，若要在①，②，③，④四个区域中的某个区域处添加一个同样的正方形，使它与阴影部分组成的新图形是中心对称图形，则这个正方形应该添加在（）

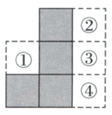A、区域①处 B、区域②处 C、区域③处 D、区域④处

查看试题解析
3. 下列运算正确的是（　　）

A、a³•a²＝a⁶ B、2a（3a﹣1）＝6a²﹣1 C、x³+x³＝2x³ D、（3a²）²＝6a⁴

查看试题解析
4. 实数a ， b ， c ， d在数轴上的对应点的位置如图所示.若 $b + d = 0$ ，则下列结论中正确的是（）

A、 $b + c > 0$ B、 $\frac{c}{a} > 1$ C、 $a d > b c$ D、 $| a | > | d |$

查看试题解析
5. 如图，点O为线段AB的中点，点B，C，D到点O的距离相等，连接AC，BD．则下面结论不一定成立的是（）

A、∠ACB=90° B、∠BDC=∠BAC C、AC平分∠BAD D、∠BCD+∠BAD=180°

查看试题解析
6. 已知一个二次函数图象经过 $P_{1} (1 ， y_{1})$ ， $P_{2} (2 ， y_{2})$ ， $P_{3} (3 ， y_{3})$ ， $P_{4} (4 ， y_{4})$ 四点，若 $y_{3} < y_{2} < y_{4}$ ，则 $y_{1} ， y_{2} ， y_{3} ， y_{4}$ 的最值情况是（）

A、 $y_{3}$ 最小， $y_{1}$ 最大 B、 $y_{3}$ 最小， $y_{4}$ 最大 C、 $y_{1}$ 最小， $y_{4}$ 最大 D、无法确定

查看试题解析

二、填空题

7. 截止2020年3月31日，中国红十字会总会机关和中国红十字基金会共接受用于新冠肺炎疫情防控社会捐赠款物约211000万元．将数211000万用科学记数法表示应为元．

查看试题解析
8.
将一副三角尺按如图所示的方式放置，使含30°角的三角尺的短直角边和含45°角的三角尺的一条直角边重合，则∠1的度数是 .

查看试题解析
9. 《九章算术》是中国古代重要的数学著作，其中“盈不足术”记载：今有共买鸡，人出九，盈十一；人出六，不足十六．问人数鸡价各几何？译文：今有人合伙买鸡，每人出九钱，会多出11钱；每人出6钱，又差16钱．问人数、买鸡的钱数各是多少？设人数为x ，买鸡的钱数为y ，可列方程组为．

查看试题解析
10. 已知 $x = 1$ 是方程 $x^{2} + b x - 2 = 0$ 的一个根，则方程的另一个根是．

查看试题解析
11. 如图，四边形 $A B C D$ 是一张正方形纸片，其面积为 $25 c m^{2}$ ．分别在边 $A B$ ， $B C$ ， $C D$ ， $D A$ 上顺次截取 $A E = B F = C G = D H = a c m (A E > B E)$ ，连接 $E F$ ， $F G$ ， $G H$ ， $H E$ ．分别以 $E F$ ， $F G$ ， $G H$ ， $H E$ 为轴将纸片向内翻折，得到四边形 $A_{1} B_{1} C_{1} D_{1}$ ，若四边形 $A_{1} B_{1} C_{1} D_{1}$ 的面积为 $9 c m^{2}$ ，则 $a =$ ．

查看试题解析
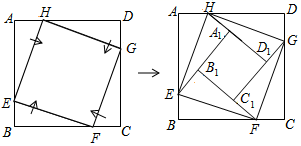12. 在 $△ A B C$ 中， $∠ C = 90 °$ ， $B C = 9 ， A C = 12$ ，点D为边AC的中点，点P为边BC上任意一点，若将 $△ C D P$ 沿DP折叠得 $△ E D P$ ，若点E落在 $△ A B C$ 的中位线所在直线上，则CP= ．

查看试题解析

三、解答题

13.

(1)、因式分解：4a³-16a；

(2)、如图，在 $△ A B C$ 中，AD平分∠BAC ， E是AD上一点，且BE＝BD；求证： $△ A B E ∽ △ A C D$ ．

查看试题解析
14. 解不等式组 ${\begin{array}{l} x + 1 \geq - 1 ① \\ \frac{x + 3}{2} \leq 2 ② \end{array}$ ．请结合题意填空，完成本题的解答．

(1)、解不等式①，得；

(2)、解不等式②，得；

(3)、把不等式①和②的解集在数轴上表示出来；

(4)、原不等式组的解集为．

查看试题解析
15. 如图，在平面直角坐标系中， A ， B是双曲线 $y = \frac{k}{x} (k \neq 0)$ 上的两点，请仅用无刻度的直尺完成下列作图（保留作图痕迹）．

(1)、在图1中画出一条与AB相等的线段；

(2)、在图2中画出一个菱形．

查看试题解析
16. 小平的爸爸积极参加社区抗疫志愿服务工作．根据社区安排，志愿者被随机分到A组（体温检测）、B组（便民代购）和C组（环境消杀）．

(1)、小平爸爸被分到A组的概率是多少；

(2)、小平的班主任肖老师也参加了该社区的志愿者队伍，试用画树状图或列表的方法表示所有可能的结果，并求出肖老师和小平的爸爸被分到同一组的概率．

查看试题解析
17. 图1是货物传送机械上的一种翻转装置，它可以使物体在传送带上实现翻转．图2是其截面简化示意图，已知连杆OA=50cm，载物直角面A-B-C中∠ABC=90°，其中点O固定，点B在水平杆OM上左右滑动，AB=BC=30cm．当载物面BC与水平杆OM重合时为初始位置，载物面BC与水平杆OM垂直时完成翻转．

(1)、直接写出点B与点O的之间距离d的取值范围是；

(2)、当点B由初始位置向右滑动10cm时，求载物面BC与水平杆OM的夹角∠CBM的度数．（结果精确到0.1°，参考数据：sin80.6°≈0.95，cos80.6°≈0.30，tan80.6°≈3.18．）

查看试题解析
18. 如图，将一张 $R t △ A B C$ 纸板的直角顶点放在 $C (2 ， 1)$ 处，两直角边 $B C$ ， $A C$ 分别与 $x$ ， $y$ 轴平行( $B C > A C$ )，纸板的另两个定点A，B恰好是直线 $y_{1} = k x + 5$ 与双曲线 $y_{2} = \frac{m}{x}$ $(m > 0)$ 的交点．

(1)、求m和k的值；

(2)、将此 $R t △ A B C$ 纸板向下平移，当双曲线 $y_{2} = \frac{m}{x}$ $(m > 0)$ 与 $R t △ A B C$ 纸板的斜边所在直线只有一个公共点时，求 $R t △ A B C$ 纸板向下平移的距离．

查看试题解析
19. 数字经济便捷了人们的生活，扫码支付随处可见．张阿姨为了解自己家庭小额（100元及以下）扫码支付的费用使用情况，整理了2021年3月12日这一天的小额扫码支付明细与3月份第2周的小额扫码支付费用分类统计表如下：

请根据以上信息回答下列问题：

(1)、请计算3月12日小额扫码支付金额的平均值；

(2)、3月份第2周小额扫码支付费用分类统计表中a= ， b=；

(3)、补全第2周小额扫码支付费用扇形统计图（图中已刻有圆周的二十等分点）；

(4)、请预估张阿姨2021年（按52周计算）小额扫码支付费用中“C：日常饮食”类别大约需要支出多少钱？

查看试题解析
20. 如图，AB是⊙O的直径，OD垂直于弦AC于点E，且交⊙O于点D，F是BA延长线上一点，若∠CDB=∠BFD．

(1)、求证：FD是⊙O的一条切线；

(2)、若AB=10，AC=8，求DF的长．

查看试题解析
21. 有若干张全等的矩形卡纸．如图所示，用8张矩形卡纸可拼成如图1的大矩形；也可拼成如图2 的正方形，但中间还留有一个边长为8cm的小正方形．

(1)、求每张卡纸的长和宽．

(2)、在每张卡纸上，可以按图3裁剪出5个全等矩形，或按图4裁剪出3个全等矩形和10个全等正三角形（裁剪后边角料不再利用）．用这些裁剪后的卡纸来制作正三棱柱盒子，每个正三棱柱盒子是由3个矩形侧面和2个正三角形底面组成；请通过计算说明，做好的正三棱柱盒子，最大能放入直径为多少cm的球体物品？（ $\sqrt{3} \approx 1.732$ ，结果精确到0.1）

(3)、现有14张卡纸，按第（2）问中的方法裁剪好，制作成正三棱柱盒子，使裁剪出的侧面和底面恰好全部用完，14张卡纸是否能满足这个要求？若能满足，求所做的正三棱柱盒子的个数；若不能满足，则至少要增加多少张卡纸，才能满足要求？请说明你的理由．

查看试题解析
22. 在边长为8的等边 $△$ ABC中，点D是边AB上的一动点，点E在边AC上，且CE = 2AD ，射线DE绕点D顺时针旋转60°交BC边于F ．

(1)、如图1，求证：∠AED = ∠BDF；

(2)、如图2，在射线DF上取DP=DE ，连接BP ，
①求∠DBP的度数；

②取边BC的中点M ，当PM取最小值时，求AD的长.

查看试题解析
23. 如图1，已知抛物线C₁： $y_{1} = x^{2} - 2 x + n + 2$ (n为正整数)的顶点为A ，与y轴交于点C ，抛物线C₂： $y_{2} = {(x + n)}^{2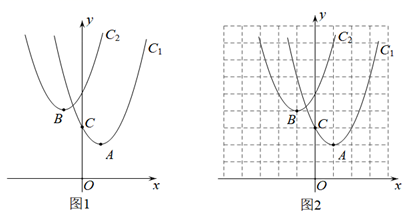} + 2 n + 2$ 的顶点为B.

(1)、当n＝1时，直接写出A点和C点的坐标

(2)、随着n值的变化，解答下列问题：
①判断点C是否在直线AB上？并说明理由；

②当BC=2AC时，求n的值．

(3)、如图2，在抛物线C₂上任取一点D ，在射线CD上取点P ，使DP＝CD ．
①当点D在抛物线C₂上运动时，在图中描出相应的点P ，再用平滑的曲线连接起来，猜想该曲线是哪种曲线？；

②直接写出该曲线的表达式．（用含n的式子表示）

查看试题解析