山西省晋中市灵石县2020-2021学年七年级下学期数学期中试卷
试卷更新日期:2021-06-25 类型:期中考试
一、选择题(每小题3分,共30分)
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 下列图形中,由AB∥CD,能得到∠1=∠2的是( )A、
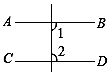 B、
B、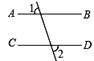 C、
C、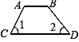 D、
D、 3. 下面是芳芳同学计算(a•a2)3的过程:
3. 下面是芳芳同学计算(a•a2)3的过程:解:(a•a2)3=a3•(a2)3…①
=a3•a6…②
=a9…③
则步骤①②③依据的运算性质分别是( )
A、积的乘方,幂的乘方,同底数幂的乘法 B、幂的乘方,积的乘方,同底数幂的乘法 C、同底数幂的乘法,幂的乘方,积的乘方 D、幂的乘方,同底数幂的乘法,积的乘方4. 圆的周长公式是 ,那么在这个公式中,关于变量和常量的说法正确的是( )A、2是常量,C、 、r是变量 B、2π是常量,C、r是变量 C、2是常量,r是变量 D、2是常量,C、r是变量5. 下列说法中正确的是( )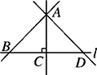
①过点A有且只有一条直线AC垂直于直线l;
②线段AC的长是点A到直线l的距离;
③线段AB,AC,AD中,线段AC最短,根据是两点之间线段最短;
④线段AB,AC,AD中,线段AC最短,根据是垂线段最短.
A、1个 B、2个 C、3个 D、4个6. =( )A、 B、 C、-4 D、47. 如图所示,已知 ,则图中 ,这是根据( )
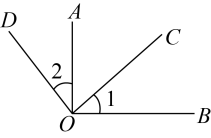 A、直角都相等 B、等角的余角相等 C、同角的余角相等 D、同角的补角相等8. 观察下列两个多项式相乘的运算过程:
A、直角都相等 B、等角的余角相等 C、同角的余角相等 D、同角的补角相等8. 观察下列两个多项式相乘的运算过程: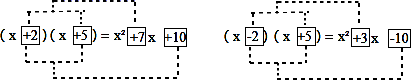
根据你发现的规律,若(x+a)(x+b)=x2-7x+12,则a,b的值可能分别是( )
A、-3,4 B、3,-4 C、-3,-4 D、3,49. 如图,直线AB与CD相交于点E,∠CEB=50°,EF⊥AE,则∠DEF的度数为( )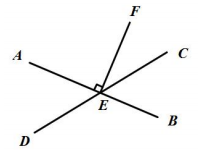 A、130° B、140° C、150° D、160°10. 如图1是一个边长分别为2x,2y的长方形纸片(x>y),沿长方形纸片的两条对称轴剪开,得到四块形状和大小都相同的小长方形,拼成如图2所示的一个正方形,则中间空白部分的面积是( )
A、130° B、140° C、150° D、160°10. 如图1是一个边长分别为2x,2y的长方形纸片(x>y),沿长方形纸片的两条对称轴剪开,得到四块形状和大小都相同的小长方形,拼成如图2所示的一个正方形,则中间空白部分的面积是( ) A、(x-y)2 B、(x+y)2 C、x·y D、x2-y2
A、(x-y)2 B、(x+y)2 C、x·y D、x2-y2二、填空题(每题3分,共15分)
-
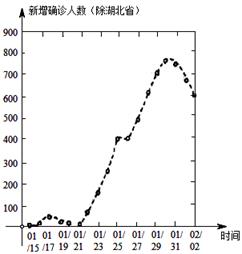
11. 某种钢管随着温度每变化1℃,每米钢管的长度就会变化0.0000118m,把0.0000118用科学记数法表示为 .12. 计算:(﹣0.125)2020×82021= .13. 如图是2020年1月15日至2月2日全国(除湖北省)新冠肺炎新增确诊人数的变化曲线,则下列说法:①自变量为时间,因变量为确诊总人数;②1月23号,新增确诊人数约为150人;③1月25号和1月26号,新增确诊人数基本相同;④1月30号之后,预测新增确诊人数呈下降趋势,其中正确的是 . (填上你认为正确的说法的序号)
 14. 如图,直线a、b相交于点O,下列说法:①若∠1=∠2,则a⊥b;②若∠1=∠3,则a⊥b;③若∠1+∠3=180°,则a⊥b;④若∠1+∠2=180°,则a⊥b.其中正确的有(填序号)
14. 如图,直线a、b相交于点O,下列说法:①若∠1=∠2,则a⊥b;②若∠1=∠3,则a⊥b;③若∠1+∠3=180°,则a⊥b;④若∠1+∠2=180°,则a⊥b.其中正确的有(填序号)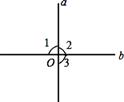 15. 如图,已知∠1=75°,将直线m平行移动到直线n的位置,则∠2﹣∠3=°.
15. 如图,已知∠1=75°,将直线m平行移动到直线n的位置,则∠2﹣∠3=°.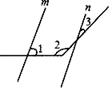
三、解答题(共75分)
-
16. 计算题:(1)、(2)、(3)、先化简,再求值 ,其中 , .17. 小华同学在学习整式乘法时发现,如果合理地使用乘法公式可以简化运算,于是如下计算题她是这样做的:

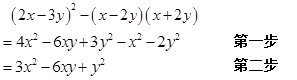
(1)、小华在此题的计算中运用了哪些乘法公式,请用字母表示出;(2)、小禹看到小华的做法后,对她说:“你做错了,在第一步运用公式时出现了错误,你好好检查一下.”小华仔细检查后自己找到了如下一处错误:
小禹看到小华的改错后说:“你还有错没有改出来.”
小华还有哪些错误没有改出来?请你帮助小华把第一步中的其他错误圈画出来,再完成此题的正确解答过程.
18. 如图,在△ABC中,∠B=67°,D为边AB上一点.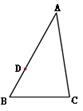 (1)、实践操作:利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法)(2)、过点D作DE∥BC,交AC边于点E,求∠ADE的度数.19. 请把以下说理过程补充完整:
(1)、实践操作:利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法)(2)、过点D作DE∥BC,交AC边于点E,求∠ADE的度数.19. 请把以下说理过程补充完整:如图,AB∥CD,∠C=∠D,如果∠1=∠2,那么∠E与∠C
互为补角吗?说说你的理由.
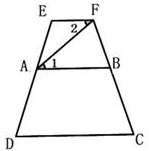
解:因为∠1=∠2,
根据 ▲ ,
所以EF∥ ▲ .
又因为AB∥CD,
根据 ▲ ,
所以EF∥ ▲ .
根据 ▲ ,
所以∠E+ ▲ = ▲ °.
又因为∠C=∠D,
所以∠E+ ▲ = ▲ °,
所以∠E与∠C互为补角.
20. 某公交车每月的支出费用为4000元,每月的乘车人数x(人)与每月利润(利润=收入费用﹣支出费用)y(元)的变化关系如表所示(每位乘客的公交票价是固定不变的).x(人)
500
1000
1500
2000
2500
3000
…
y(元)
﹣3000
﹣2000
﹣1000
0
1000
2000
…
(1)、上表中反映的两个变量之间的关系,哪个是自变量?哪个是因变量?(2)、观察表中数据可知,每月乘客量达到多少人以上时,该公交车才不会亏损?(3)、当每月乘车人数为4000人时,每月利润为多少元?简述你得出结论的理由。21. 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.如果∠1=∠2,且∠3=115°,求∠ACB的度数.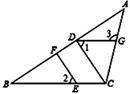 22. 综合与实践
22. 综合与实践我们知道,图形是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,而运用代数思想也能巧妙的解决一些图形问题.
小明同学用如图1所示不同颜色的正方形与长方形纸片拼成了一个如图2所示的正方形.
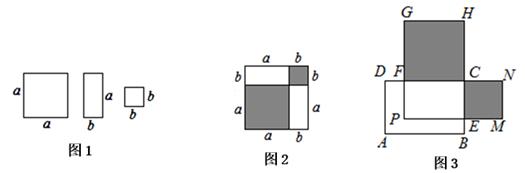 (1)、用不同的代数式表示图2中阴影部分的面积,写出你能得到的等式,并用乘法公式说明这个等式成立;(2)、小明想到利用(1)中得到的等式可以完成了下面这道题:
(1)、用不同的代数式表示图2中阴影部分的面积,写出你能得到的等式,并用乘法公式说明这个等式成立;(2)、小明想到利用(1)中得到的等式可以完成了下面这道题:如果x满足(6-x)(x-2)=3.求(6-x)2+(x-2)2 的值。
小明想:如果设6-x=m,x-2=n ,那要求的式子就可以写成m2+n2了
请你按照小明的思路完成这道题目。
(3)、如图3,在长方形ABCD中,AB=10,BC=6,E、F是BC, CD上的点,且BE=DF=x,分别以FC,CE为边在长方形ABCD外侧作正方形CFGH和 CEMN,若长方形 CEPF的面积为40,求图中阴影部分的面积和.23. 综合与探究【问题情境】
王老师组织同学们开展了探究三角之间数量关系的数学活动.
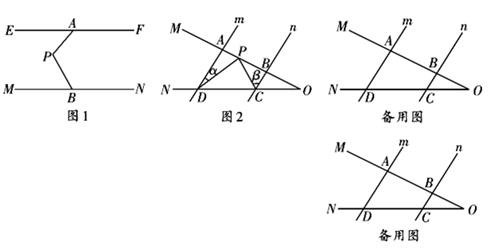 (1)、如图1,EF∥MN,点A、B分别为直线EF、MN上的一点,点P为平行线间一点,请直接写出∠PAF、∠PBN和∠APB之间的数量关系;(2)、【问题迁移】
(1)、如图1,EF∥MN,点A、B分别为直线EF、MN上的一点,点P为平行线间一点,请直接写出∠PAF、∠PBN和∠APB之间的数量关系;(2)、【问题迁移】如图2,射线OM与射线ON交于点O,直线m∥n,直线m分别交OM、ON于点A、D,直线n分别交OM、ON于点B、C,点P在射线OM上运动.
①当点P在A、B(不与A、B重合)两点之间运动时,设∠ADP=∠α,∠BCP=∠β.则∠CPD,∠α,∠β之间有何数量关系?请说明理由;
②若点P不在线段AB上运动时(点P与点A、B、O三点都不重合),请你画出满足条件的所有图形并直接写出∠CPD,∠α,∠β之间的数量关系.