江西省抚州市南城县2020-2021学年七年级下学期数学期中试卷
试卷更新日期:2021-06-25 类型:期中考试
一、选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项)
-
1. 某种新冠病毒变异后的直径为0.00000018米,0.00000018米用科学记数法表示为( )A、1.8×10-5米 B、0.18×10-6米 C、1.8×10-7米 D、18×10-8米2. 在网课期间,七年级的小明学习到“用尺规作一个角等于已知角”时发现自己没有圆规,放学后他匀速跑步到附近的超市,在超市买好圆规后,再沿原路匀速步行回家,他离家的距离y与离家时间x的关系图象大致是( )A、
 B、
B、 C、
C、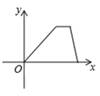 D、
D、 3. 乐乐观察“抖空竹“时发现,可以将某一时刻的情形抽象成数学问题:如图,已知AB∥CD,∠BAE=92°,∠DCE=115°,则∠E的度数是( )
3. 乐乐观察“抖空竹“时发现,可以将某一时刻的情形抽象成数学问题:如图,已知AB∥CD,∠BAE=92°,∠DCE=115°,则∠E的度数是( )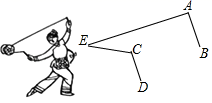 A、32° B、28° C、26° D、23°4. 下列运算正确的是( )A、 B、 C、 D、5. 下列说法中不正确的是( )A、三条直线a,b,c若a∥b,b∥c,则a∥c B、在同一平面内,若直线a∥b,c⊥a,则c⊥b
A、32° B、28° C、26° D、23°4. 下列运算正确的是( )A、 B、 C、 D、5. 下列说法中不正确的是( )A、三条直线a,b,c若a∥b,b∥c,则a∥c B、在同一平面内,若直线a∥b,c⊥a,则c⊥bC、在同一平面内,过一点有且只有一条直线与已知直线垂直 D、在同一平面内,过一点有且只有一条直线与已知直线平行6. 若 , ,则M与N的大小关系是( )A、M>N B、M<N C、M=N D、无法确定二、填空题(本大题共6小题,每小题3分,共18分)
-
7. 若 , ,则 =.8. 根据表格中的数据规律,当x=-4时,y的值是.
X
…
-2
-1
0
1
2
3
…
y
…
-8
-1
0
1
8
27
…
9. 如果a,b,c是整数,且 ,那么我们规定一种记号(a,b)=c,例如 ,那么记作(3,9)=2,根据以上规定,求(2, )= .10. “过点P作直线b , 使b∥a”,小明的作图痕迹如图所示,他的作法的依据是 . 11. 已知 (n=1,2,3,…),记 , , ,则 = .12. 若 ,则a=.
11. 已知 (n=1,2,3,…),记 , , ,则 = .12. 若 ,则a=.三、(本大题共5小题,每小题6分,共30分)
-
13. 计算:(1)、(2)、14. ,其中 ,15. 在方格纸(每个小方格都是边长为1个单位长度的正方形)中,我们把每个小正方形的顶点称为格点,已知O、A、B都是方格纸上的格点,仅利用无刻度直尺完成下列作图(注:下列求作的点都是格点).

( 1 )画线段AB、AC,使得AB⊥AC;
( 2 )过点O画线段OD,使得OD∥AB.
16. 已知 ,试求 的值.17. 甲骑自行车,乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间关系的图象如图所示,根据图象解答下列问题: (1)、谁先出发?先出发多少时间?谁先到达终点?先到多少时间?
(1)、谁先出发?先出发多少时间?谁先到达终点?先到多少时间?
(2)、分别求出甲、乙两人的行驶速度;
(3)、在什么时间段内,两人均行驶在途中?(不包括起点和终点)四、(本大题共3小题,每小题8分,共24分)
-
18. 已知 是∠ 的2倍, 的余角的3倍等于∠ 的补角,求 和∠ 的度数.19. 欢欢与乐乐两人共同计算 ,欢欢抄成 ,得到的结果为 ;乐乐抄成 ,得到的结果为 .(1)、请计算出原题的正确答案.20. 【问题发现】如图①,直线AB∥CD,E是AB与CD之间的一点,连接BE,CE,可以发现∠B+∠C=∠BEC.
 (1)、请把下面的证明过程补充完整:
(1)、请把下面的证明过程补充完整:证明:过点E作EF∥AB,
∵AB∥CD(已知),EF∥AB(辅助线的作法),
∴EF∥CD( ),
∴∠C=∠CEF( ),
∵EF∥AB(作图),
∴∠B= ▲ , ( ),
∴∠B+∠C=_ ▲ (等量代换),即∠B+∠C=∠BEC.
(2)、【拓展探究】如果点E运动到图②所示的位置,其他条件不变,进一步探究发现:∠B,∠C,∠BEC之间的关系是(3)、【解决问题】如图③,AB∥DC,∠C=120°,∠AEC=80°,请求出∠A的度数.五、(本大题共2小题,每小题9分,共18分)
-
21. 在疫情期间,南城金山口某口罩生产厂家为提高生产效益引进了新的设备,其中甲表示新设备的产量y(万个)与生产时间x(天)的关系,乙表示旧设备的产量y(万个)与生产时间x(天)的关系:
 (1)、由图象可知,新设备因工人操作不当停止生产了天;
(1)、由图象可知,新设备因工人操作不当停止生产了天;
(2)、求新、旧设备每天分别生产多少万个口罩?
(3)、在生产过程中,x为何值时,新旧设备所生产的口罩数量相同.22. 动手操作:如图①:将一副三角板中的两个直角顶点叠放在一起,其中∠A=30°,∠B=60°,∠D=∠E=45°.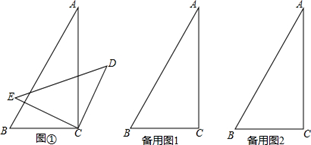 (1)、若∠BCD=150°,求∠ACE的度数;(2)、试猜想∠BCD与∠ACE的数量关系,请说明理由;(3)、若按住三角板ABC不动,绕顶点C转动三角板DCE,试探究当CD∥AB时,∠BCD等于多少度,并简要说明理由.
(1)、若∠BCD=150°,求∠ACE的度数;(2)、试猜想∠BCD与∠ACE的数量关系,请说明理由;(3)、若按住三角板ABC不动,绕顶点C转动三角板DCE,试探究当CD∥AB时,∠BCD等于多少度,并简要说明理由.六、(本大题共12分)
-
23. 若x满足 ,求 的值.
解:设 , ,
则 , ,
∴ .
请仿照上面的方法求解下面问题:(1)、若x满足 ,求 + 的值;(2)、若x满足 ,求 的值;(3)、已知正方形ABCD的边长为x,E,F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是48,分别以MF、DF作正方形MFRN和正方形GFDH,求阴影部分的面积.