辽宁省朝阳市2020-2021学年八年级下学期数学期中考试试卷
试卷更新日期:2021-06-25 类型:期中考试
一、选择题(本大题共10小题,共30分.每小题只有一个选项符合题意)
-
1. 下列根式中,是最简二次根式的是( )A、 B、 C、 D、2. 二次根式 中, 的取值范围是( )A、 B、 C、 D、3. 已知 、 、为 的三边,且满足 ,则 是( )A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等腰三角形或直角三角形4. 已知在平行四边形ABCD中,∠A=∠B+40°,则∠A的度数为( )A、35° B、70° C、110° D、140°5. 下列命题中,其逆命题成立的是有( )
①同旁内角互补,两直线平行;
②如果两个角是直角,那么它们相等;
③如果两个实数相等,那么它们的平方相等;
④如果三角形的三边长 , ,满足 ,那么这个三角形是直角三角形
A、①③④ B、①②③ C、②④ D、①④6. 下列命题中,真命题是( )A、一组对边平行,另一组对边相等的四边形是平行四边形 B、对角线互相垂直且相等的四边形是菱形 C、直角三角形中, 角所对直角边都等于斜边的一半 D、对角线相等的平行四边形是正方形7. 《九章算术》中的“方田章”论述了三角形面积的求法:“圭田术曰,半广以乘正广”,就是说:“三角形的面积=底×高 ”,我国著名的数学家秦九韶在《数书九章》中也提出了“三斜求积术”,即可以利用三角形的三条边长来求取三角形面积,用现代式子可表示为: (其中 、 、为三角形的三条边长, 为三角形的面积).如图,在平行四边形 中,已知 , ,对角线 ,则平行四边形 的面积为( )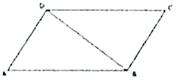 A、 B、 C、 D、8. 如图,在四边形 中,下列条件不能判定四边形 是平行四边形的是( )
A、 B、 C、 D、8. 如图,在四边形 中,下列条件不能判定四边形 是平行四边形的是( )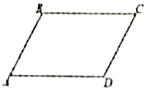 A、 , B、 , C、 , D、 ,9. 在数学拓展课《折叠矩形纸片》上,小林发现折叠矩形纸片 可以进行如下操作:①把 翻折,点 落在 边上的点 处,折痕为 ,点 在 边上;②把 翻折,点 落在 边上的点 处,折痕为 ,点 在 边上,若 , ,则 ( )
A、 , B、 , C、 , D、 ,9. 在数学拓展课《折叠矩形纸片》上,小林发现折叠矩形纸片 可以进行如下操作:①把 翻折,点 落在 边上的点 处,折痕为 ,点 在 边上;②把 翻折,点 落在 边上的点 处,折痕为 ,点 在 边上,若 , ,则 ( )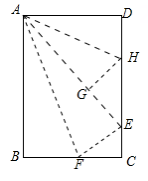 A、 B、 C、 D、10. 如图1,四边形 是菱形,对角线 , 相交于点 , , 两点同时从点 出发,以厘米/秒的速度在菱形的对角线及边上运动. , 的运动路线:点 为 ,点 为 .设运动的时间为 秒, , 间的距离为 厘米, 与 的函数关系的图象大致如图2所示,则菱形 的面积为( )
A、 B、 C、 D、10. 如图1,四边形 是菱形,对角线 , 相交于点 , , 两点同时从点 出发,以厘米/秒的速度在菱形的对角线及边上运动. , 的运动路线:点 为 ,点 为 .设运动的时间为 秒, , 间的距离为 厘米, 与 的函数关系的图象大致如图2所示,则菱形 的面积为( )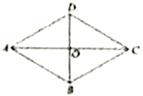
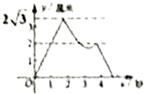
图1 图2
A、 B、 C、 D、二、填空题(18分)
-
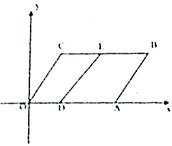
11. 若等式 成立,则 的取值范围是 .12. 已知在 中, , , ,则 的面积为 .13. 如图,在平面直角坐标系中,已知点 的坐标为 ,点 的坐标为 ,四边形 是平行四边形,点 、 份别在边 、 上,且 , .动点 、 在 的一组邻边上,以点 、 、 、 为顶点的四边形是平行四边形时,其面积为 .
 14. 如图,已知 ,点 在边 上, ,过点 作 于点 ,以 为一边在 内作等腰直角三角形 ,点 是 围成的区域(不包括各边)内的一点,过点 作 交 于点 ,作 交 于点 ,设 ,则 取值范围是.
14. 如图,已知 ,点 在边 上, ,过点 作 于点 ,以 为一边在 内作等腰直角三角形 ,点 是 围成的区域(不包括各边)内的一点,过点 作 交 于点 ,作 交 于点 ,设 ,则 取值范围是.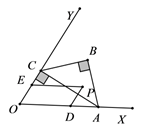 15. 如图,在边长为10的菱形 中,对角线 ,点O是线段 上的动点, 于E, 于F.则 .
15. 如图,在边长为10的菱形 中,对角线 ,点O是线段 上的动点, 于E, 于F.则 .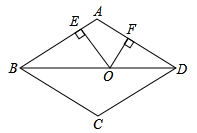 16. 如图,四边形 是矩形纸片, ,对折矩形纸片 ,使 与 重合,折痕为 ,展平后再过点B折叠矩形纸片,使点A落在 上的点N处,折痕 与 相交于点Q;再次展平,连接 ,延长 交 于点G;P为线段 上一动点 . 有如下结论:① ;② ;③ 是等边三角形;④ ;⑤H是 的中点,则 的最小值是 . 其中正确结论的序号是 .
16. 如图,四边形 是矩形纸片, ,对折矩形纸片 ,使 与 重合,折痕为 ,展平后再过点B折叠矩形纸片,使点A落在 上的点N处,折痕 与 相交于点Q;再次展平,连接 ,延长 交 于点G;P为线段 上一动点 . 有如下结论:① ;② ;③ 是等边三角形;④ ;⑤H是 的中点,则 的最小值是 . 其中正确结论的序号是 .
三、解答题(72分)
-
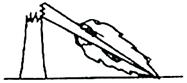
17. 计算: .18. 如图,2020年5月14日1号台风“黄蜂过后,某市体育中心附近一棵大树在高于地面3米处折断,大树顶部落在距离大树底部4米处的地面上.求这棵树折断之前的高度.
 19. 如图,四边形 中, , ,对角线 , 相交于点 ,且 .求证:四边形 是矩形.
19. 如图,四边形 中, , ,对角线 , 相交于点 ,且 .求证:四边形 是矩形. 20. 如图,在 中, , , ,垂足分别为点 、 .
20. 如图,在 中, , , ,垂足分别为点 、 .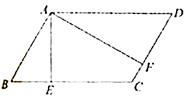 (1)、求 的度数;(2)、如果 ,求线段 的长.21. 阅读下列问题:
(1)、求 的度数;(2)、如果 ,求线段 的长.21. 阅读下列问题:; ;
以上化简的方法叫作分母有理化,仿照以上方法化简:
(1)、 ;(2)、求 的值:(3)、求 ( 为正整数)的值.22. 如图,已知 ,直线 垂直平分 ,与边 交于点 ,连接 ,过点 作 交 于点 ,连接 .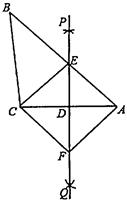 (1)、求证: ;(2)、求证:四边形 是菱形;(3)、若 , ,则菱形 的面积是多少?23. 如图1,在等边 中, ,动点 从点 出发以 的速度沿 匀速运动,动点 同时从点 出发以同样的速度沿 的延长线方向匀速运动,当点 到达点 时,点 、 同时停止运动,设运动时间为 .过点 作 于 ,以 、 为边作平行四边形 .
(1)、求证: ;(2)、求证:四边形 是菱形;(3)、若 , ,则菱形 的面积是多少?23. 如图1,在等边 中, ,动点 从点 出发以 的速度沿 匀速运动,动点 同时从点 出发以同样的速度沿 的延长线方向匀速运动,当点 到达点 时,点 、 同时停止运动,设运动时间为 .过点 作 于 ,以 、 为边作平行四边形 .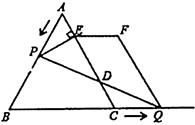
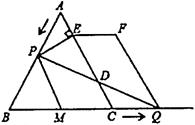
图1 图2
(1)、 , ;(用含的代数式表示)(2)、当平行四边形 为菱形时,请求出的值;(3)、如图1,连接 ,交 边于点 ,求线段 的长;(4)、如图2,取线段 的中点 ,连接 ,将 沿直线 翻折,得 ,连接 ,请求出 的最小值.