江西省抚州市南城县2020-2021学年八年级下学期数学期中考试试卷
试卷更新日期:2021-06-25 类型:期中考试
一、选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项)
-
1. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若x>y,则下列式子错误的是( )A、x+1>y+1 B、 C、﹣2x<﹣2y D、1﹣x>1﹣y3. 已知等腰三角形的一个内角等于 ,则该三角形的一个底角是( )A、 B、 或 C、 或 D、4. 如图,经过点 的直线 与直线 相交于点 ,则不等式 的解集为( )
2. 若x>y,则下列式子错误的是( )A、x+1>y+1 B、 C、﹣2x<﹣2y D、1﹣x>1﹣y3. 已知等腰三角形的一个内角等于 ,则该三角形的一个底角是( )A、 B、 或 C、 或 D、4. 如图,经过点 的直线 与直线 相交于点 ,则不等式 的解集为( ) A、 B、 C、 D、5. 如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D.CD=3,则BC的长为( )
A、 B、 C、 D、5. 如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D.CD=3,则BC的长为( )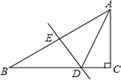 A、6 B、9 C、6 D、36. 如图,已知△ABC中高AD恰好平分边BC,∠B=30°,点P是BA延长线上一点,点O是线段AD上一点且OP=OC,下面的结论:
A、6 B、9 C、6 D、36. 如图,已知△ABC中高AD恰好平分边BC,∠B=30°,点P是BA延长线上一点,点O是线段AD上一点且OP=OC,下面的结论:
①AC=AB;②∠APO+∠DCO=30°;
③△OPC是等边三角形; ④AC=AO+AP.
其中正确的为( )
A、①②③ B、①②④ C、①③④ D、①②③④二、填空题(本大题共6小题,每小题3分,共18分)
-
7. 在 中, , ,则 .8. 若点A(a,3)与点B(﹣4,b)关于原点对称,则a﹣b= .9. 用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”第一步应假设.10. 已知a、b是等腰 的两边长,且满足 ,则该等腰三角形的周长为 .11. 若关于 的不等式 的正整数解只有3个,则 的取值范围是 .12. 在Rt 中,∠ABC=90°,AB=3,BC=4,过点B的直线把 分割成两个三角形,使其中只有一个是等腰三角形,则AP= .
三、解答题(本大题共5小题,每小题6分,共30分)
-
13. 解不等式和不等式组,并把它的解集在数轴上表示出来.(1)、(2)、解不等式组14. 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1cm,将Rt△ABC绕点A逆时针旋转得到Rt ,使点 落在AB边上,连接 ,求 的长 .
 15. 如图,在正方形网格中,△ABC的顶点在格点上.请仅用无刻度直尺完成以下作图(保留作图痕迹).
15. 如图,在正方形网格中,△ABC的顶点在格点上.请仅用无刻度直尺完成以下作图(保留作图痕迹).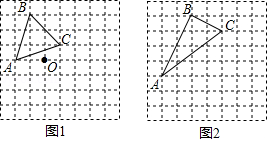
( 1 )在图1中,作 关于点O对称的 ;
( 2 )在图2中,作 绕点A顺时针旋转一定角度后,顶点仍在格点上的 .
16. 若关于x、y的二元一次方程组 的解满足x+y<2,求a的取值范围.17. 如图,在平面直角坐标系中, 的三个顶点分别为A(-4,-1),B(-2,-4),C(-1,-2). (1)、①请画出 向右平移5个单位长度后得到的 ;
(1)、①请画出 向右平移5个单位长度后得到的 ;②请画出 关于直线 对称的 ;
(2)、线段 的长是.四、(本大题共3小题,每小题8分,共24分)
-
18. 如图,直线 经过点 , .
 (1)、求直线 的解析式;(2)、若直线 与直线 相交于点C,求点C的坐标;(3)、根据图象,写出关于x的不等式 的解集.19. 如图, 由 绕点 按逆时针方向旋转 得到,且点B的对应点D恰好落在BC的延长线上,AD,EC相交于点P.
(1)、求直线 的解析式;(2)、若直线 与直线 相交于点C,求点C的坐标;(3)、根据图象,写出关于x的不等式 的解集.19. 如图, 由 绕点 按逆时针方向旋转 得到,且点B的对应点D恰好落在BC的延长线上,AD,EC相交于点P. (1)、求∠BDE的度数;(2)、 是 延长线上的点,且∠CDF=∠DAC.判断DF和PF的数量关系,并证明.20. 已知,如图△ABC为等边三角形,AE=CD,AD、BE相交于点P.
(1)、求∠BDE的度数;(2)、 是 延长线上的点,且∠CDF=∠DAC.判断DF和PF的数量关系,并证明.20. 已知,如图△ABC为等边三角形,AE=CD,AD、BE相交于点P. (1)、求证: ;(2)、求∠BPQ的度数;(3)、若 于Q,PQ=6,PE=2,求BE的长.
(1)、求证: ;(2)、求∠BPQ的度数;(3)、若 于Q,PQ=6,PE=2,求BE的长.五、(本大题共2小题,每小题9分,共18分)
-
21. 如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
 (1)、出发2秒后,求PQ的长;(2)、当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?(3)、当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.22. 端午节快到了,小明准备买粽子过节,若在南城某超市购买2盒甲品牌粽子和3盒乙品牌粽子需支付380元,而在某团购群购买5盒甲品牌粽子和4盒乙品牌粽子需支付520元,对比发现,甲品牌粽子每盒的团购价相当于超市价的八折,乙品牌粽子每盒的团购价相当于超市价的七五折.(1)、甲、乙两种品牌粽子每盒的超市价分别是多少元?(2)、小明要打算在团购群购买这两种品牌的粽子,其中乙品牌粽子比甲品牌粽子多2盒,总花费不超过1000元,问小明最多能买多少盒甲品牌粽子?
(1)、出发2秒后,求PQ的长;(2)、当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?(3)、当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.22. 端午节快到了,小明准备买粽子过节,若在南城某超市购买2盒甲品牌粽子和3盒乙品牌粽子需支付380元,而在某团购群购买5盒甲品牌粽子和4盒乙品牌粽子需支付520元,对比发现,甲品牌粽子每盒的团购价相当于超市价的八折,乙品牌粽子每盒的团购价相当于超市价的七五折.(1)、甲、乙两种品牌粽子每盒的超市价分别是多少元?(2)、小明要打算在团购群购买这两种品牌的粽子,其中乙品牌粽子比甲品牌粽子多2盒,总花费不超过1000元,问小明最多能买多少盒甲品牌粽子?六、解答题(本大题共12分)
-
23. 在 中, ,D是直线BC上一点,以AD为一条边在AD的右侧作 ,使 , ,连接CE.(1)、如图,当点D在BC延长线上移动时,若 ,则 .(2)、设 , .
①当点D在BC延长线上移动时, 与 之间有什么数量关系?请说明理由;
②当点D在直线BC上不与B,C两点重合移动时, 与 之间有什么数量关系?请画出相应的图形,直接写出你的结论.
