四川省广安市2021年中考数学试卷
试卷更新日期:2021-06-24 类型:中考真卷
一、单选题
-
1. 16的平方根是( )A、 ±4 B、4 C、±8 D、82. 下列运算中,正确的是( )A、 B、 C、 D、3. 到2021年6月3日,我国31个省(自治区、直辖市)和新疆生产建设兵团,累计接种新冠疫苗约7.05亿剂次,请将7.05亿用科学记数法表示( )A、 B、 C、 D、4. 下列几何体的主视图既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 关于 的一元二次方程 有实数根,则 的取值范围是( )A、 且 B、 C、 且 D、6. 下列说法正确的是( )A、为了了解全国中学生的心理健康情况,选择全面调查 B、在一组数据7,6,5,6,6,4,8中,众数和中位数都是6 C、“若 是实数,则 ”是必然事件 D、若甲组数据的方差 ,乙组数据的方差 ,则乙组数据比甲组数据稳定7. 若点 , , 都在反比例函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、8. 如图,将 绕点 逆时针旋转 得到 ,若 且 于点 ,则 的度数为( )
5. 关于 的一元二次方程 有实数根,则 的取值范围是( )A、 且 B、 C、 且 D、6. 下列说法正确的是( )A、为了了解全国中学生的心理健康情况,选择全面调查 B、在一组数据7,6,5,6,6,4,8中,众数和中位数都是6 C、“若 是实数,则 ”是必然事件 D、若甲组数据的方差 ,乙组数据的方差 ,则乙组数据比甲组数据稳定7. 若点 , , 都在反比例函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、8. 如图,将 绕点 逆时针旋转 得到 ,若 且 于点 ,则 的度数为( ) A、 B、 C、 D、9. 如图,公园内有一个半径为18米的圆形草坪,从 地走到 地有观赏路(劣弧 )和便民路(线段 ).已知 、 是圆上的点, 为圆心, ,小强从 走到 ,走便民路比走观赏路少走( )米.
A、 B、 C、 D、9. 如图,公园内有一个半径为18米的圆形草坪,从 地走到 地有观赏路(劣弧 )和便民路(线段 ).已知 、 是圆上的点, 为圆心, ,小强从 走到 ,走便民路比走观赏路少走( )米. A、 B、 C、 D、10. 二次函数 的图象如图所示,有下列结论:① ,② ,③ ,④ ,正确的有( )
A、 B、 C、 D、10. 二次函数 的图象如图所示,有下列结论:① ,② ,③ ,④ ,正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
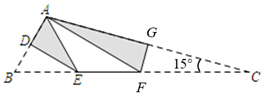
11. 在函数y= 中,自变量x的取值范围是 .12. 若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是 .13. 一个三角形的两边长分别为3和5,第三边长是方程x2-6x+8=0的根,则三角形的周长为.14. 若 、 满足 ,则代数式 的值为.15. 如图,将三角形纸片 折叠,使点 、 都与点 重合,折痕分别为 、 .已知 , , ,则 的长为.
 16. 如图,在平面直角坐标系中, 轴,垂足为 ,将 绕点 逆时针旋转到 的位置,使点 的对应点 落在直线 上,再将 绕点 逆时针旋转到 的位置,使点 的对应点 也落在直线 上,以此进行下去……若点 的坐标为 ,则点 的纵坐标为.
16. 如图,在平面直角坐标系中, 轴,垂足为 ,将 绕点 逆时针旋转到 的位置,使点 的对应点 落在直线 上,再将 绕点 逆时针旋转到 的位置,使点 的对应点 也落在直线 上,以此进行下去……若点 的坐标为 ,则点 的纵坐标为.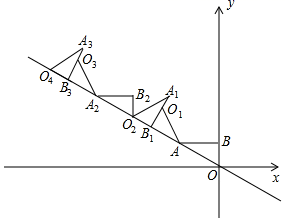
三、解答题
-
17. 计算: .18. 先化简: ,再从-1,0,1,2中选择一个适合的数代入求值.19. 如图,四边形 是菱形,点 、 分别在边 、 的延长线上,且 .连接 、 .
求证: .
 20. 如图,一次函数 的图象与反比例函数 的图象交于 , 两点.
20. 如图,一次函数 的图象与反比例函数 的图象交于 , 两点.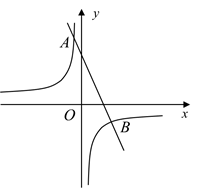 (1)、求一次函数和反比例函数的解析式;(2)、点 在 轴上,且满足 的面积等于4,请直接写出点 的坐标.21. 在中国共产党成立100周年之际,我市某中学开展党史学习教育活动.为了了解学生学习情况,在七年级随机抽取部分学生进行测试,并依据成绩(百分制)绘制出以下两幅不完整的统计图.请根据图中信息回答下列问题:
(1)、求一次函数和反比例函数的解析式;(2)、点 在 轴上,且满足 的面积等于4,请直接写出点 的坐标.21. 在中国共产党成立100周年之际,我市某中学开展党史学习教育活动.为了了解学生学习情况,在七年级随机抽取部分学生进行测试,并依据成绩(百分制)绘制出以下两幅不完整的统计图.请根据图中信息回答下列问题: (1)、本次抽取调查的学生共有人,扇形统计图中表示 等级的扇形圆心角度数为.(2)、 等级中有2名男生,2名女生.从中随机抽取2人参加学校组织的知识问答竞赛,请用画树状图或列表的方法,求恰好抽到一男一女的概率.22. 国庆节前,某超市为了满足人们的购物需求,计划购进甲、乙两种水果进行销售.经了解,甲种水果和乙种水果的进价与售价如下表所示:
(1)、本次抽取调查的学生共有人,扇形统计图中表示 等级的扇形圆心角度数为.(2)、 等级中有2名男生,2名女生.从中随机抽取2人参加学校组织的知识问答竞赛,请用画树状图或列表的方法,求恰好抽到一男一女的概率.22. 国庆节前,某超市为了满足人们的购物需求,计划购进甲、乙两种水果进行销售.经了解,甲种水果和乙种水果的进价与售价如下表所示:水果单价
甲
乙
进价(元/千克)
售价(元/千克)
20
25
已知用1200元购进甲种水果的重量与用1500元购进乙种水果的重量相同.
(1)、求 的值;(2)、若超市购进这两种水果共100千克,其中甲种水果的重量不低于乙种水果重量的3倍,则超市应如何进货才能获得最大利润,最大利润是多少?23. 如图①、图②分别是某种型号跑步机的实物图与示意图.已知跑步机手柄 与地面 平行,踏板 长为 , 与地面 的夹角 ,支架 长为 , ,求跑步机手柄 所在直线与地面 之间的距离.(结果精确到 .参考数据: , , , ) 24. 下图是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点为格点,线段 的端点都在格点上.要求以 为边画一个平行四边形,且另外两个顶点在格点上.请在下面的网格图中画出4种不同的设计图形.
24. 下图是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点为格点,线段 的端点都在格点上.要求以 为边画一个平行四边形,且另外两个顶点在格点上.请在下面的网格图中画出4种不同的设计图形.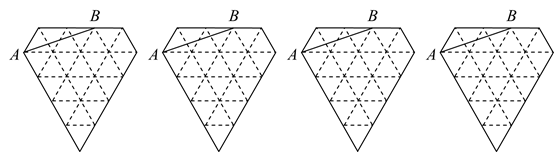 25. 如图, 是 的直径,点 在 上, 的平分线 交 于点 ,过点 作 ,交 的延长线于点 ,延长 、 相交于点 .
25. 如图, 是 的直径,点 在 上, 的平分线 交 于点 ,过点 作 ,交 的延长线于点 ,延长 、 相交于点 . (1)、求证: 是 的切线;(2)、若 的半径为5, ,求 的长.26. 如图,在平面直角坐标系中,抛物线 的图象与坐标轴相交于 、 、 三点,其中 点坐标为 , 点坐标为 ,连接 、 .动点 从点 出发,在线段 上以每秒 个单位长度向点 做匀速运动;同时,动点 从点 出发,在线段 上以每秒1个单位长度向点 做匀速运动,当其中一点到达终点时,另一点随之停止运动,连接 ,设运动时间为 秒.
(1)、求证: 是 的切线;(2)、若 的半径为5, ,求 的长.26. 如图,在平面直角坐标系中,抛物线 的图象与坐标轴相交于 、 、 三点,其中 点坐标为 , 点坐标为 ,连接 、 .动点 从点 出发,在线段 上以每秒 个单位长度向点 做匀速运动;同时,动点 从点 出发,在线段 上以每秒1个单位长度向点 做匀速运动,当其中一点到达终点时,另一点随之停止运动,连接 ,设运动时间为 秒. (1)、求 、 的值;(2)、在 、 运动的过程中,当 为何值时,四边形 的面积最小,最小值为多少?(3)、在线段 上方的抛物线上是否存在点 ,使 是以点 为直角顶点的等腰直角三角形?若存在,请求出点 的坐标;若不存在,请说明理由.
(1)、求 、 的值;(2)、在 、 运动的过程中,当 为何值时,四边形 的面积最小,最小值为多少?(3)、在线段 上方的抛物线上是否存在点 ,使 是以点 为直角顶点的等腰直角三角形?若存在,请求出点 的坐标;若不存在,请说明理由.