湖南省衡阳市2021年中考数学试卷
试卷更新日期:2021-06-24 类型:中考真卷
一、单选题
-
1. 8的相反数是( )A、 -8 B、8 C、 D、±82. 2021年2月25日,习近平总书记庄严宣告,我国脱贫攻坚战取得全面胜利.现标准下,98990000农村贫困人口全部脱贫.数98990000用科学记数法表示为( )A、 B、 C、 D、3. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列运算结果为 的是( )A、 B、 C、 D、5. 下列计算正确的是( )A、 B、 C、 D、6. 为了向建党一百周年献礼,我市中小学生开展了红色经典故事演讲比赛.某参赛小组6名同学的成绩(单位:分)分别为:85,82,86,82,83,92.关于这组数据,下列说法错误的是( )A、众数是82 B、中位数是84 C、方差是84 D、平均数是857. 如图是由6个相同的正方体堆成的物体,它的左视图是( ).
4. 下列运算结果为 的是( )A、 B、 C、 D、5. 下列计算正确的是( )A、 B、 C、 D、6. 为了向建党一百周年献礼,我市中小学生开展了红色经典故事演讲比赛.某参赛小组6名同学的成绩(单位:分)分别为:85,82,86,82,83,92.关于这组数据,下列说法错误的是( )A、众数是82 B、中位数是84 C、方差是84 D、平均数是857. 如图是由6个相同的正方体堆成的物体,它的左视图是( ).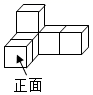 A、
A、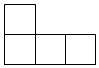 B、
B、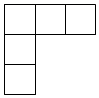 C、
C、 D、
D、 8. 如图是某商场营业大厅自动扶梯的示意图.自动扶梯 的倾斜角为 ,大厅两层之间的距离 为6米,则自动扶梯 的长约为( )( ).
8. 如图是某商场营业大厅自动扶梯的示意图.自动扶梯 的倾斜角为 ,大厅两层之间的距离 为6米,则自动扶梯 的长约为( )( ).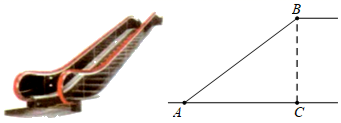 A、7.5米 B、8米 C、9米 D、10米9. 下列命题是真命题的是( ).A、正六边形的外角和大于正五边形的外角和 B、正六边形的每一个内角为 C、有一个角是 的三角形是等边三角形 D、对角线相等的四边形是矩形10. 不等式组 的解集在数轴上可表示为( )A、
A、7.5米 B、8米 C、9米 D、10米9. 下列命题是真命题的是( ).A、正六边形的外角和大于正五边形的外角和 B、正六边形的每一个内角为 C、有一个角是 的三角形是等边三角形 D、对角线相等的四边形是矩形10. 不等式组 的解集在数轴上可表示为( )A、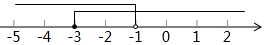 B、
B、 C、
C、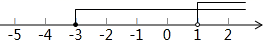 D、
D、 11. 下列说法正确的是( )A、为了解我国中学生课外阅读情况,应采取全面调查方式 B、某彩票的中奖机会是1%,买100张一定会中奖 C、从装有3个红球和4个黑球的袋子里摸出1个球是红球的概率是 D、某校有3200名学生,为了解学生最喜欢的课外体育运动项目,随机抽取了200名学生,其中有85名学生表示最喜欢的项目是跳绳,估计该校最喜欢的课外体育运动项目为跳绳的有1360人12. 如图,矩形纸片 ,点M、N分别在矩形的边 、 上,将矩形纸片沿直线 折叠,使点C落在矩形的边 上,记为点P,点D落在G处,连接 ,交 于点Q,连接 .下列结论:①四边形 是菱形;②点P与点A重合时, ;③ 的面积S的取值范围是 .其中所有正确结论的序号是( )
11. 下列说法正确的是( )A、为了解我国中学生课外阅读情况,应采取全面调查方式 B、某彩票的中奖机会是1%,买100张一定会中奖 C、从装有3个红球和4个黑球的袋子里摸出1个球是红球的概率是 D、某校有3200名学生,为了解学生最喜欢的课外体育运动项目,随机抽取了200名学生,其中有85名学生表示最喜欢的项目是跳绳,估计该校最喜欢的课外体育运动项目为跳绳的有1360人12. 如图,矩形纸片 ,点M、N分别在矩形的边 、 上,将矩形纸片沿直线 折叠,使点C落在矩形的边 上,记为点P,点D落在G处,连接 ,交 于点Q,连接 .下列结论:①四边形 是菱形;②点P与点A重合时, ;③ 的面积S的取值范围是 .其中所有正确结论的序号是( )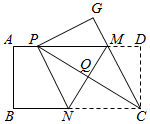 A、①②③ B、①② C、①③ D、②③
A、①②③ B、①② C、①③ D、②③二、填空题
-
13. 要使二次根式 有意义,则x的取值范围是 .
14. 计算: =15. 因式分解: .16. 底面半径为3,母线长为4的圆锥的侧面积为.(结果保留 )17. “绿水青山就是金山银山”.某地为美化环境,计划种植树木6000棵.由于志愿者的加入,实际每天植树的棵树比原计划增加了25%,结果提前3天完成任务.则实际每天植树棵.18. 如图1,菱形 的对角线 与 相交于点O,P、Q两点同时从O点出发,以1厘米/秒的速度在菱形的对角线及边上运动.点P的运动路线为 ,点Q的运动路线为 .设运动的时间为x秒,P、Q间的距离为y厘米,y与x的函数关系的图象大致如图2所示,当点P在 段上运动且P、Q两点间的距离最短时,P、Q两点的运动路程之和为厘米.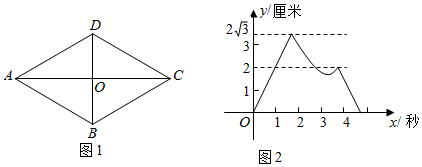
三、解答题
-
19. 计算: .20. 如图,点A、B、D、E在同一条直线上, .求证: .
 21. “垃圾分类工作就是新时尚”,为了改善生态环境,有效利用垃圾剩余价值,2020年起,我市将生活垃圾分为四类:厨余垃圾、有害垃圾、可回收垃圾、其他垃圾.某学习研究小组在对我市垃圾分类实施情况的调查中,绘制了生活垃圾分类扇形统计图,如图所示.
21. “垃圾分类工作就是新时尚”,为了改善生态环境,有效利用垃圾剩余价值,2020年起,我市将生活垃圾分为四类:厨余垃圾、有害垃圾、可回收垃圾、其他垃圾.某学习研究小组在对我市垃圾分类实施情况的调查中,绘制了生活垃圾分类扇形统计图,如图所示.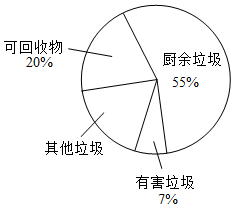 (1)、图中其他垃圾所在的扇形的圆心角度数是度;(2)、据统计,生活垃圾中可回收物每吨可创造经济总价值约为0.2万元.若我市某天生活垃圾清运总量为500吨,请估计该天可回收物所创造的经济总价值是多少万元?(3)、为了调查学生对垃圾分类知识的了解情况,某校开展了相关知识竞赛,要求每班派2名学生参赛.甲班经选拔后,决定从2名男生和2名女生中随机抽取2名学生参加比赛,求所抽取的学生中恰好一男一女的概率.22. 如图,点E为正方形 外一点, ,将 绕A点逆时针方向旋转 得到 的延长线交 于H点.
(1)、图中其他垃圾所在的扇形的圆心角度数是度;(2)、据统计,生活垃圾中可回收物每吨可创造经济总价值约为0.2万元.若我市某天生活垃圾清运总量为500吨,请估计该天可回收物所创造的经济总价值是多少万元?(3)、为了调查学生对垃圾分类知识的了解情况,某校开展了相关知识竞赛,要求每班派2名学生参赛.甲班经选拔后,决定从2名男生和2名女生中随机抽取2名学生参加比赛,求所抽取的学生中恰好一男一女的概率.22. 如图,点E为正方形 外一点, ,将 绕A点逆时针方向旋转 得到 的延长线交 于H点. (1)、试判定四边形 的形状,并说明理由;(2)、已知 ,求 的长.23. 如图是一种单肩包,其背带由双层部分、单层部分和调节扣构成.小文购买时,售货员演示通过调节扣加长或缩短单层部分的长度,可以使背带的长度(单层部分与双层部分长度的和,其中调节扣所占长度忽略不计)加长或缩短,设双层部分的长度为 ,单层部分的长度为 .经测量,得到下表中数据.
(1)、试判定四边形 的形状,并说明理由;(2)、已知 ,求 的长.23. 如图是一种单肩包,其背带由双层部分、单层部分和调节扣构成.小文购买时,售货员演示通过调节扣加长或缩短单层部分的长度,可以使背带的长度(单层部分与双层部分长度的和,其中调节扣所占长度忽略不计)加长或缩短,设双层部分的长度为 ,单层部分的长度为 .经测量,得到下表中数据.双层部分长度
2
8
14
20
单层部分长度
148
136
124
112
(1)、根据表中数据规律,求出y与x的函数关系式;(2)、按小文的身高和习惯,背带的长度调为 时为最佳背带长.请计算此时双层部分的长度;(3)、设背带长度为 ,求L的取值范围.24. 如图, 是 的直径,D为 上一点,E为 的中点,点C在 的延长线上,且 . (1)、求证: 是 的切线;(2)、若 ,求 的长.25. 如图, 的顶点坐标分别为 ,动点P、Q同时从点O出发,分别沿x轴正方向和y轴正方向运动,速度分别为每秒3个单位和每秒2个单位,点P到达点B时点P、Q同时停止运动.过点Q作 分别交 、 于点M、N,连接 、 .设运动时间为t(秒).
(1)、求证: 是 的切线;(2)、若 ,求 的长.25. 如图, 的顶点坐标分别为 ,动点P、Q同时从点O出发,分别沿x轴正方向和y轴正方向运动,速度分别为每秒3个单位和每秒2个单位,点P到达点B时点P、Q同时停止运动.过点Q作 分别交 、 于点M、N,连接 、 .设运动时间为t(秒).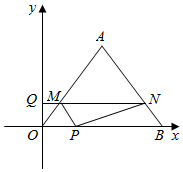 (1)、求点M的坐标(用含t的式子表示);(2)、求四边形 面积的最大值或最小值;(3)、是否存在这样的直线l,总能平分四边形 的面积?如果存在,请求出直线l的解析式;如果不存在,请说明理由;(4)、连接 ,当 时,求点N到 的距离.26. 在平面直角坐标系中,如果一个点的横坐标与纵坐标相等,则称该点为“雁点”.例如 ……都是“雁点”.
(1)、求点M的坐标(用含t的式子表示);(2)、求四边形 面积的最大值或最小值;(3)、是否存在这样的直线l,总能平分四边形 的面积?如果存在,请求出直线l的解析式;如果不存在,请说明理由;(4)、连接 ,当 时,求点N到 的距离.26. 在平面直角坐标系中,如果一个点的横坐标与纵坐标相等,则称该点为“雁点”.例如 ……都是“雁点”.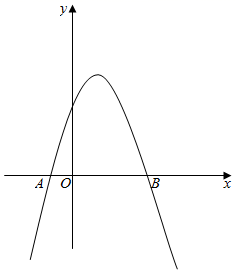 (1)、求函数 图象上的“雁点”坐标;(2)、若抛物线 上有且只有一个“雁点”E,该抛物线与x轴交于M、N两点(点M在点N的左侧).当 时.
(1)、求函数 图象上的“雁点”坐标;(2)、若抛物线 上有且只有一个“雁点”E,该抛物线与x轴交于M、N两点(点M在点N的左侧).当 时.①求c的取值范围;
②求 的度数;
(3)、如图,抛物线 与x轴交于A、B两点(点A在点B的左侧),P是抛物线 上一点,连接 ,以点P为直角顶点,构造等腰 ,是否存在点P,使点C恰好为“雁点”?若存在,求出点P的坐标;若不存在,请说明理由.