新疆维吾尔自治区、生产建设兵团2021年中考数学试卷
试卷更新日期:2021-06-24 类型:中考真卷
一、单选题
-
1. 下列实数是无理数的是( )A、-2 B、1 C、 D、22. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
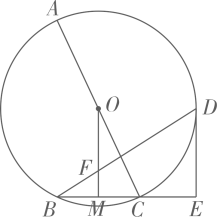
D、 3. 不透明的袋子中有3个白球和2个紅球,这些球除颜色外无其他差別,从袋子中随机摸出1个球,恰好是白球的概率( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,直线DE过点A,且 .若 , ,则 的度数为( )
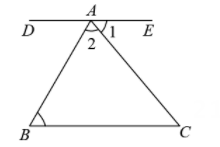
3. 不透明的袋子中有3个白球和2个紅球,这些球除颜色外无其他差別,从袋子中随机摸出1个球,恰好是白球的概率( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,直线DE过点A,且 .若 , ,则 的度数为( )
 A、 B、 C、 D、6. 关于x的一元二次方程x2﹣4x+3=0的解为( )A、x1=﹣1,x2=3 B、x1=1,x2=﹣3 C、x1=1,x2=3 D、x1=﹣1,x2=﹣37. 如图,在Rt 中, , , , 于点D,E是AB的中点,则DE的长为( )
A、 B、 C、 D、6. 关于x的一元二次方程x2﹣4x+3=0的解为( )A、x1=﹣1,x2=3 B、x1=1,x2=﹣3 C、x1=1,x2=3 D、x1=﹣1,x2=﹣37. 如图,在Rt 中, , , , 于点D,E是AB的中点,则DE的长为( )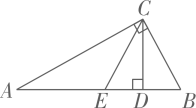 A、1 B、2 C、3 D、48. 某校举行篮球赛,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.八年级一班在16场比赛中得26分.设该班胜x场,负y场,则根据题意,下列方程组中正确的是( )A、 B、 C、 D、9. 如图,在矩形ABCD中, , .点P从点A出发,以2cm/s的速度在矩形的边上沿 运动,当点P与点D重合时停止运动.设运动的时间为 (单位:s), 的面积为S(单位: ),则S随t变化的函数图象大致为( )
A、1 B、2 C、3 D、48. 某校举行篮球赛,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.八年级一班在16场比赛中得26分.设该班胜x场,负y场,则根据题意,下列方程组中正确的是( )A、 B、 C、 D、9. 如图,在矩形ABCD中, , .点P从点A出发,以2cm/s的速度在矩形的边上沿 运动,当点P与点D重合时停止运动.设运动的时间为 (单位:s), 的面积为S(单位: ),则S随t变化的函数图象大致为( )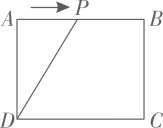 A、
A、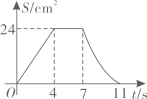 B、
B、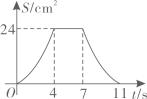 C、
C、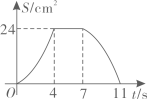 D、
D、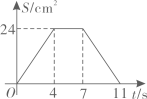
二、填空题
-
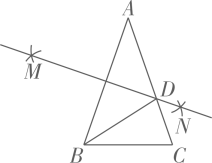
10. 今年“五一”假期,新疆铁路累计发送旅客795 900人次.用科学记数法表示795 900为.11. 不等式2x﹣1>3的解集为12. 四边形的外角和等于.13. 若点 , 在反比例函 的图象上,则 (填“>“<”或“=”).14. 如图,在 中, , ,分别以点A,B为圆心,大于 的长为半径作弧,两弧相交于M,N两点,作直线MN交AC于点D,连接BD,则 .
 15. 如图,已知正方形ABCD边长为1,E为AB边上一点,以点D为中心,将 按逆时针方向旋转得 ,连接EF,分別交BD,CD于点M,N.若 ,则 .
15. 如图,已知正方形ABCD边长为1,E为AB边上一点,以点D为中心,将 按逆时针方向旋转得 ,连接EF,分別交BD,CD于点M,N.若 ,则 .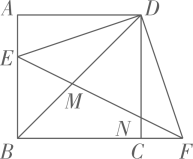
三、解答题
-
16. 计算: .17. 先化简,再求值: ,其中 .18. 如图,在矩形ABCD中,点E在边BC上,点F在BC的延长线上,且 .
求证:
 (1)、 ;(2)、四边形AEFD是平行四边形.19. 某校为了增强学生的疫情防控意识.组织全校2000名学生进行了疫情防控知识竞赛.从中随机抽取了n名学生的竞赛成绩(满分100分),分成四组:A: ;B: ;C: ;D: ,并绘制出如下不完整的统计图:
(1)、 ;(2)、四边形AEFD是平行四边形.19. 某校为了增强学生的疫情防控意识.组织全校2000名学生进行了疫情防控知识竞赛.从中随机抽取了n名学生的竞赛成绩(满分100分),分成四组:A: ;B: ;C: ;D: ,并绘制出如下不完整的统计图: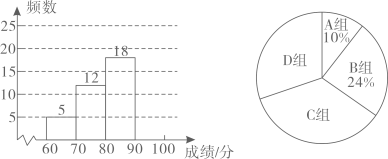 (1)、填空:n=;(2)、补全频数分布直方图;(3)、抽取的这n名学生成绩的中位数落在组;(4)、若规定学生成绩 为优秀.估算全校成绩达到优秀的人数.20. 如图,楼顶上有一个广告牌AB,从与楼BC相距15 m的D处观测广告牌顶部A的仰角为 ,观测广告牌底部B的仰角为 ,求广告牌AB的高度(结果保留小数点后一位,参考数据: , , , , ).
(1)、填空:n=;(2)、补全频数分布直方图;(3)、抽取的这n名学生成绩的中位数落在组;(4)、若规定学生成绩 为优秀.估算全校成绩达到优秀的人数.20. 如图,楼顶上有一个广告牌AB,从与楼BC相距15 m的D处观测广告牌顶部A的仰角为 ,观测广告牌底部B的仰角为 ,求广告牌AB的高度(结果保留小数点后一位,参考数据: , , , , ).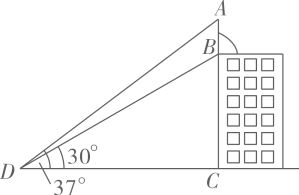 21. 如图,一次函数 与反比例函数 的图象交于点 , .
21. 如图,一次函数 与反比例函数 的图象交于点 , .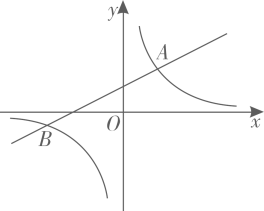 (1)、求反比例函数和一次函数的解析式;(2)、判断点 是否在一次函数 的图象上,并说明理由;(3)、直接写出不等式 的解集.
(1)、求反比例函数和一次函数的解析式;(2)、判断点 是否在一次函数 的图象上,并说明理由;(3)、直接写出不等式 的解集.